1. Introduction
Gamma radiation interaction is the most accurate, convenient and a non destructive method of determining the various characteristics of the material. With increasing the use of radioactive isotopes and applications of radiations in many fields such as industry, agriculture, medicine, technology and research, there seems a need to study in depth gamma ray analysis of every material. Gamma ray interaction depends on the extent of absorption or scattering, incident energy, nature of the target material and also on the geometrical conditions. The knowledge of gamma ray interaction parameters [1] of the material provides not only better understanding of the degradation of energy but also a basis for safe handling of what might be admittedly harmful material. The accurate determination of interaction parameters is essential before a given material is used in any field. Mass attenuation coefficient [2] - [9] is the basic parameter for understanding the gamma ray interaction with matter. It gives fraction of the energy scattered or absorbed due to interaction with matter. A large number of photon attenuation measurements, calculations and compilations of various elements have been available at National Institute of Standards and Technology, Gaithers- burg USA (J.H. Hubbell group) [10] . Different other workers have calculated attenuation coefficients in different categories such as building materials, alloys, marbles, glasses, biological materials and other composite materials.
Effective atomic number (Zeff) is another useful important parameter for a composite material. It measures the effect of chemical composition, atomic number as well as abundance of each element in the sample. Therefore, effective atomic number [11] - [16] plays a vital role in the multi-elemental material analysis. According to Hine (1952), “effective atomic number of a material composed of several elements cannot be expressed by a single number and various atomic numbers of elements have to be weighted differently”. Following Hine, several authors have conducted Zeff studies in various composite materials such as alloys, soils, perspex and bakelite, compounds and thermoluminescent dosimetric compounds etc. However, in literature, only a limited amount of work has been reported for Zeff studies of different types of slags.
Electron density (electron/g) and half value layer (HVL) are two other useful parameters for understanding the interaction of gamma ray. The degradation or attenuation of gamma rays are directly related with electron density [17] [18] as it represents the probability of electron’s presence in the material. Half value layer (HVL) determines the thickness required to reduce the intensity to a safe level. It also determines the effectiveness of a material to be used for shielding radiation. Many workers have studied electron densities and HVL for shielding characteristics of materials such as fatty acids, lead oxide, barites and lead-flyash concretes.
On the basis of these computed and measured interaction parameters, an attempt has been made and it is proposed to use iron and steel slags for the shielding of nuclear radiation in preference to flyash.
2. Theory
2.1. Attenuation Coefficients
A parallel beam of monochromatic radiation is attenuated in matter, its intensity decreases from I0 to I according to Lambert-Beer law
(1)
where ρ is density and x is thickness of the material. μ (cm−1) is linear attenuation coefficient. Equation (1), can be written as,
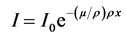
where 
(cm2/g) is called mass attenuation coefficient, denoted by
.
For a composite material,
(2)
where 
and 
are weight fraction and mass attenuation coefficient, respectively, of the constituent element i.
2.2. Effective Atomic Number (Zeff)
This is another important parameter for the interpretation of attenuation of radiation by composite materials. As atomic number is not constant for different interaction processes in different energy regions, the various atomic numbers of elements present in the sample have to be weighted differently. The effective atomic number, (Zeff), can be defined through the following relations;
The total molecular cross-section 
can be calculated using the relation
where 
is molar mass. NA is Avogadro number; ni and Ai are the number of formula units and atomic weight respectively of ith element.
The total atomic cross-section 
is given by
.
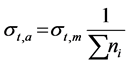The total electronic cross-section 
is given by
where 
is the fractional abundance of ith element.
(3)
where 
is the average atomic cross section and 
is the average electronic cross section.
2.3. Electron Density (Ne)
Electron density is defined as number of electrons per gram in the material. It can be determined from the following relations;
![]()
(4)
where ![]()
is molar mass. NA is Avogadro number and ni is the number of formula units of ith element. (![]()
) is the cross section/electron related to atomic cross section (σa) as![]()
.
The atomic cross section and mass attenuation coefficient (![]()
) are related as ![]()
2.4. Half Value Layer (HVL)
In an attenuating medium, half value layer (or half thickness) is defined as the thickness of any material which can reduce the intensity of incident gamma ray beam to one half of its original value.
HVL is related to the linear attenuation coefficient μ (cm−1) by the following relation
![]()
. (5)
It is measured in units of length.
3. Experimental Details
3.1. Collection and Preparation of Mixture
Both Steel slag and Iron slags materials are by product of steel and iron industries respectively. Steel slag is taken from Modern Steel plant, situated at Mandi Gobindgarh whereas Iron slags (soft and hard type) have been collected from factories situated in local industrial area of Patiala. Large production and cheap availability of these materials pose a serious threat to our environment. That is why present work is undertaken and an attempt has been made to study the intensity of gamma radiation with the mixture of Steel slag (SS) and Iron slag with an intent to investigate the possibility of their utilization and disposal [19] .
The test specimens were prepared according to specifications Bureau of Indian Standards. First, these materials were crushed and grinded separately so as to get powdered form. Both types of iron slags (soft and hard) are mixed together in equal proportions to get what may be called Mixed Iron Slag (MIS). Then steel slag is replaced by 0%, 10% 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90% in Mixed Iron Slag content by weight. The materials were weighed accurately and mixed properly. Cube moulds were filled with these mixtures and kept for 48 h in a casting room at a temperature of 25˚C after which they were demoulded. The prepared ten samples were named as IS0, IS1, IS2, IS3, IS4, IS5, IS6, IS7, IS8 and IS9. A Pure flyash sample is also prepared for comparing results.
3.2. Chemical Composition
The chemical composition of Steel slag and MIS was determined by Energy dispersive X ray analysis (EDX) available at Thapar University, Patiala. The weight percentage of different elements present in Steel slag-Iron mixtures are shown in Table 1. For comparison of their attenuation properties, weight percentage of pure flyash is given in Table 2.
3.3. Measurements of Transmitted Gamma Ray Spectra
Narrow beam y-ray transmission geometry was used for the attenuation measurements of prepared specimens. The experimental setup of geometry is shown in Figure 1. The source was enclosed in a lead container with one face aperture 5 mm, placed behind the source collimator. Three collimators with apertures 6 mm, 4 mm and 2.8 mm were placed with their front faces at a distance of 100 mm, 240 mm and 515 mm from the source respectively. The width of each
![]()
Table 1. Weight percentage of Steel slag-Iron mixtures.
![]()
Table 2. Weight percentage of flyash.
![]()
Figure 1. Experimental setup for narrow beam transmission geometry.
collimator was 40 mm. The prepared samples were cubes of each side 5 cm. Samples were positioned on specimen holder at a distance of 290 mm from the source. The distance between source and detector was held at 585 mm. The detector was surrounded with proper lead shielding so as to prevent the scattered radiations from nearby objects reaching the detector. The total scatter acceptance angle (θsc) [20] is the sum of the incidence beam divergence (θin) and angle subtended by exit collimation (θout). For the present geometry, the incidence beam divergence was 1.63˚ and the acceptance angle at the detector was 0.72˚. Overall scatter acceptance angle was 2.6˚. For this value of scatter acceptance angle, the scattered radiation reaching the detector can cause a ray-sum error of 0.5% - 1.0% which falls within the tolerating limits.
The model 802 scintillation detector of 3 × 3 NaI(Tl) type was used in the study. It was enclosed in a hermetically sealed assembly which includes a high resolution NaI(TI) crystal, a PMT with a pre-amplifier, an internal magnetic/ light shield, an aluminium housing and a 14-pin connector. The reliability and stability of the geometrical setup was tested using aluminium as a reference absorber at 662 keV. The spectrum was recorded for sufficient long time so as to reduce statistical error in counts less than 0.3%. The best resolution 7.5% was obtained for the 662 keV gamma ray from Cs-137 source. The background counts recorded for the same time were subtracted from each spectrum. To stop the fluorescence X-rays of lead entering in the detector, the lead shield was lined on the inside and with brass and aluminium sheets outside. The experiment was conducted at constant low temperature to avoid shifting of spectrum peak.
4. Results and Discussion
The incident (Io) and transmitted (I) y-ray intensities have been measured for experimentally determining the values of mass attenuation coefficients of specimens. The experimental values of mass attenuation coefficient obtained using Equation (1) are enlisted in Table 3, together with the theoretical values, calculated using the winXCOM computer program [21] . The maximum errors in mass attenuation coefficient were calculated from errors in the incident (Io) and transmitted (I) intensities, mass density (![]()
) and thickness (t) using the propagation of error formula:
![]()
Table 3. Mass attenuation values for Steel slag-Iron samples at various energies.
![]()
where t is the sample thickness in centimetres, and are the errors in the intensities Io, I, density and thickness t of the sample respectively. It was found that the estimated error in experimental measurements was less than 3.7%. The experimental results are in good agreement with the theoretical results within estimated errors.
The linear attenuation coefficient μ (cm−1) is shown graphically as a function of given photon energies in Figure 2. As density of samples do not change so much with increase in steel slag, therefore, mass attenuation coefficients as well as linear attenuation coefficients remain constant because first is independent of density of the material and depend only upon the chemical composition of the material The variations in (![]()
) values and linear attenuation coefficients (μ) at different energies are interpreted as being due to the dominance and Z-de- pendence of different partial photon interaction processes in different energy regions. In low energy region (60,136 KeV), the variation of μm (Total) and μ (cm−1) is mainly due to Photo electric process and also less, but significantly due to coherent scattering. Photo electric process is Z4−5 dependent whereas coherent scattering has Z2−3 dependence. Moreover, sharp decrease in both μm and μ (cm−1) in low energy region is due to the fact that Photo electric cross section is inversely proportional to E3.5 in the intermediate energy region (662 KeV - 1332 KeV).
For the (MIS + SS) specimens, effective atomic numbers have been determined from the mass attenuation coefficients. The obtained values of effective atomic numbers are shown graphically in Figure 3. The results in present investigations clearly support the view points of Hine (1952). The trend in variation
![]()
Figure 2. Variation of Linear attenuation coefficients with energy.
![]()
Figure 3. Variation of Zeff with energy.
![]()
Table 4. Electron density values (×1023) of Steel slag-Iron samples at various energies.
of Zeff with variation in steel slag content at given energies (60, 136, 662, 1173, 1332 KeV) is same as that of μm or μ (cm−1). With the increase in steel slag content, effective atomic numbers of specimens do not change much. The present results are in line with the results of Lingam et al. (1984), Parthasaradhi (1968) and Modi et al. (1991) in the covered energy region. In the energy region of 662 to 1332 KeV, the values of effective atomic number are almost constant which is also in line with the viewpoint of El-Kateb and Abdul Hamid.
The computed electron density values using Equation (4) are shown in Table 4. The electron density for all the specimens varies in the range of ((2.93 - 4.24) × 1023) electrons per unit gram of the material.
The values of half value layer (HVL) of the prepared specimens were computed using Equation (5) and are shown graphically in Figure 4.
From the obtained results, it is observed that, half value layer increases with increase in energy and with decrease in steel slag content. To assess the shielding ability [22] of a material, half value layer (HVL) is inversely related to shielding effectiveness. With the increase in energy, (HVL) increases, because to reduce intensity of incident gamma radiations to one half, more thickness of the target will be required. Also, with decrease in steel slag content, (HVL), increases slightly. This is attributed to small decrease in linear attenuation coefficients with decrease in steel slag content (Figure 2). It is clear that, (HVL), for any (MIS + SS) sample is very much lower than Pure Flyash at all the given energies. It means that (MIS + SS) mixtures are better in gamma ray shielding than Pure Flyash at all the given energies. The mass attenuation coefficients, μm of all the samples were also computed with the help of a state of-the-art convenient computer programme WinXCOM, initially developed by Berger and Hubble and later modified to window version by Gerward et al. (2004). This programme was run on a personal computer. For the computation of![]()
, the chemical composition of each sample was supplied to the programme. The mass attenuation coefficient ![]()
in cm2/g of each sample was computed. From the results obtained, other interaction parameters were also computed.
5. Applications/Utilizations
Both slags are environmentally hazardous materials and are being produced in huge amounts every day. So, their utilization and disposal is a matter of serious concern. Taking into consideration their attenuation abilities, these materials can be used for radiation shielding if properly compacted or admixed with concrete. Slag mixed concretes are most suitable especially where huge structures are required e.g., Nuclear reactors, Underground bunkers for protection against Nuclear experiments or testing Nuclear weapons etc. These structures become
![]()
Figure 4. Variation of (HVL) of (MIS + SS) with incident energy.
more durable, economical as well as eco-friendly when slags are used in concretes. The reason is that concrete develop micro-cracks due to higher level of hydration and porosity. Also, variation in composition and large water content leads to decrease of density and structure strength of concretes. As slags contain silica, which converts free lime present in concretes into insoluble calcium silicate hydrates that decreases heat of hydration, thereby reducing cracks in concretes. It also provides strength to concretes at later ages.
6. Conclusion
The performance of a concrete radiation shield with slags is improved effectively. Though, flyash is also used as an aggregate in making radiation shields its density is far less than slag. Thus, effective attenuation ability of slag is more than that of flyash. The comparison of gamma ray shielding properties of steel slag + iron slag mixtures with Pure Flyash at various gamma ray energies shows that the mixtures are more suitable than Pure Flyash in shielding gamma radiations. Keeping in view these facts and their utilization, steel slag + iron slag mixture is more appropriate for making shields as well as in other construction activities.