Peak-to-Average Power Ratio Performance Analysis for Orthogonal Chirp Division Multiplexing Multicarrier Systems Based on Discrete Fractional Cosine Transform ()
1. Introduction
Orthogonal Frequency Division Multiplexing (OFDM) is proved to be an effective method to eliminate Inter-Symbol Interference (ISI) and simply equalizing the quasi-static multipath fading channels using a single tape equalizer [1] [2] . Consequently OFDM is the main physical layer for several wireless standards and the new Digital Video Broadcasting (DVB) [3] . Recently, the worldwide interoperability for microwave access (WiMAX) technology designed to provide simultaneous mobile broadband services at very high vehicular speeds (beyond 100 km/h), resulting in a huge demand for the DVB handheld (DVB-H) systems. These new applications face the OFDM with the doubly dispersive channels (time-frequency fading channels) which cause the loss of the subcarriers orthogonality leading to Inter-Carrier Interference (ICI) and degrading the OFDM system performance [4] [5] [6] [7] resulting in the requirement of a complex equalizer. In order to improve the multicarrier system performance, the subcarriers frequencies should be time-varying in order to deal with the fast time-frequency distortion of the channel.
Using the Discrete Fractional Fourier Transform (DFrFT) or the Discrete Fractional Cosine Transform (DFrCT) to replace the Fast Fourier Transformer (FFT) in multicarrier systems was introduced in [8] [9] [10] [11] and both showed the system capability to reduce the effects of Doppler frequency spreads. The resulting DFrCT-OCDM system is a block transfer system wherein the carriers are chirp signals which are orthogonal to each other. Although both of the traditional OFDM and the DFrCT-OCDM systems cannot diagonalize the doubly dispersive channel matrix thus requiring complex equalizers such as MMSE equalizer, the DFrCT-OCDM can significantly compensate the power leakage from subcarriers through the channel matrix thus reducing the ICI and yielding better performance [11] .
All multicarrier systems suffer from the problem of high PAPR, which is caused due to the addition of large number of independently modulated signals. Hence, to avoid nonlinear distortion and spectral spreading of the eliminated transmitted signal, highly linear amplifiers operating with a large back-off have to be used which is less efficient. This may have a negative effect on battery lifetime in mobile applications [12] like WiMAX and DVB-H. The hard limiting of the transmitted signal may be considered as another source for noise as the in-band distortion will increase the errors and the out of band distortion will reduce the spectral efficiency [13] . Therefore, reducing the PAPR is always an important factor for practical system design and implementation. Recently, there have been some work to evaluate the PAPR for the case of the OFDM system [14] [15] [16] [17] and for the DFrFT-OCDM based system [18] [19] . Following this line of research, we extend the PAPR study to the case of the DFrCT-OCDM based system.
In this paper, we investigate the PAPR performance of multicarrier systems based on the DFrCT, showing that these systems are more robust multicarriers under doubly dispersive fading channels comparing to the traditional OFDM and the DFrFT-OCDM systems. In this paper an evaluation for the PAPR performance of a multicarrier system based on the fractional cosine transform (FrCT) is introduced and then compared with DFrFT and FFT. Moreover, Applying the SLAM technique over these systems is provided to understand the behaviour of these systems when applying SLAM. The theoretical limits supported by the simulations results show that we can suggest that the DFrCT-OCDM system outperforms OFDM system in the proposed scenario, however, for a large value of sub-carriers, both systems become obtain similar performance.
Finally, in this work, we introduce the conventional methods of PAPR reduction to the fractional domain, resulting in the fact that it is possible to extend techniques developed for OFDM system (such as SLM technique) for DFrCT-OCDM systems.
The rest of the paper is organized as follows. In Section 2, multicarrier systems are introduced. In Section 3, the PAPR problem is provided. In Section 4, experimental and evaluation results are provided for comparing the PAPR performance of the proposed DFrCT-OCDM to that of the OFDM system and the FrFT-OCDM. In Section 5, the paper is concluded.
2. Multicarrier Systems
A multicarrier signal is the sum of a great number of independently modulated signals onto sub-channels of equal bandwidth. In continuous-time and discrete time versions, the transmitter of a multicarrier system can be presented as shown in Figure 1. At the transmitter, a serial-to-parallel buffer segments the binary information into blocks. Then, each block of data is mapped according to the modulation scheme (e.g., BPSK, QPSK, QAM etc.), resulting in a vector of N complex-value subcarrier coefficients.
Let us represent the collection of all data symbols , as a vector
, as a vector  that will be labeled a data block. The complex baseband representation of a multicarrier signal consisting of N subcarriers of OFDM system is given by Equation (1):
that will be labeled a data block. The complex baseband representation of a multicarrier signal consisting of N subcarriers of OFDM system is given by Equation (1):
 (1)
(1)
where  is the subcarrier spacing,
is the subcarrier spacing,  and NT denotes the useful data block period. The subcarriers are chosen to be orthogonal (i.e.
and NT denotes the useful data block period. The subcarriers are chosen to be orthogonal (i.e. ).
).
For Discrete Fractional Fourier Transform based orthogonal chirp division multiplexing (DFrFT-OCDM) multicarrier system the transmitted signal is given by Equation (2):
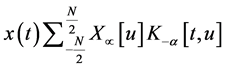 (2)
(2)
where  is the transformation Kernel of the DFrFT and is related to the DFrFT
is the transformation Kernel of the DFrFT and is related to the DFrFT
![]()
Figure 1. A block diagram of the multicarrier system transmitter.
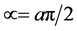 with
with .
. 
 (3)
(3)
where . In particular, if
. In particular, if  , (i.e., a = 1) then Equation (3) will be reduced to the general expression for a baseband OFDM transmitted signal.
, (i.e., a = 1) then Equation (3) will be reduced to the general expression for a baseband OFDM transmitted signal.
For Discrete Fractional Cosine Transform based orthogonal chirp division multiplexing (DFrCT-OCDM) multicarrier system the transmitted signal which is given by [20] shown in Equation (4)
 (4)
(4)
where  is the transformation Kernel of the DFrCT and
is the transformation Kernel of the DFrCT and ![]() is related to the DFrFT
is related to the DFrFT ![]() with
with![]() .
. ![]()
![]() (5)
(5)
where![]() .
.
For practical considerations, a discrete-time representation of these systems is needed. Assume Nyquist rate is used for sampling the samples of the transmitted vector x can be expressed as shown in Equation (6):
![]() (6)
(6)
![]() is the unitary
is the unitary ![]() matrix where N is the number of samples and
matrix where N is the number of samples and ![]() denotes the Hermitian transpose of the transformation matrix
denotes the Hermitian transpose of the transformation matrix![]() , where
, where ![]() can represent any of the previously produced transformations.
can represent any of the previously produced transformations.
OFDM and DFrFT-OCDM Systems under Doubly Dispersive Fading Channel
Figure 2 illustrates the OFDM system, and Equation (7) gives the transmitted data vector ![]() in the
in the ![]() OFDM symbol:
OFDM symbol:
![]() (7)
(7)
where its samples in the frequency domain, permuted by the binary matrix ![]() which assigns a data vector
which assigns a data vector ![]() to
to ![]() subcarriers, of which only
subcarriers, of which only ![]() are active according to Equation (8):
are active according to Equation (8):
![]() (8)
(8)
where ![]() is an
is an ![]() matrix with zero entries, and
matrix with zero entries, and ![]() is an
is an ![]() identity matrix. The vector
identity matrix. The vector![]() is calculated from Equation (9):
is calculated from Equation (9):
![]() (9)
(9)
where ![]() is used to denote the
is used to denote the ![]() -point unitary IDFT matrix.
-point unitary IDFT matrix.
The doubly dispersive channel can be modelled by the time variant discrete impulse response![]() , where
, where ![]() is the time instant and
is the time instant and ![]() is the time delay. Model justification can be found in more details in [5] [21] [22] and it can be expressed in the form of (time-variant, circular) convolution matrix by Equation (10):
is the time delay. Model justification can be found in more details in [5] [21] [22] and it can be expressed in the form of (time-variant, circular) convolution matrix by Equation (10):
![]() (10)
(10)
Assuming causal channel and the cyclic prefix ![]() is longer than the maximum delay spread
is longer than the maximum delay spread![]() , the received samples for the
, the received samples for the ![]() OFDM symbol after discarding the CP can be given by Equation (11):
OFDM symbol after discarding the CP can be given by Equation (11):
![]() (11)
(11)
where ![]() are samples of white Gaussian noise (AWGN) with variance
are samples of white Gaussian noise (AWGN) with variance![]() . In stationary conditions,
. In stationary conditions, ![]() is circulant, and can be decoupled by the DFT matrix. Received subcarriers are demodulated using the DFT as shown in Equation (12)
is circulant, and can be decoupled by the DFT matrix. Received subcarriers are demodulated using the DFT as shown in Equation (12)
![]() (12)
(12)
where ![]() is the DFT matrix and
is the DFT matrix and ![]() is the received signal after demodulation by the DFT matrix. The equaliser matrix
is the received signal after demodulation by the DFT matrix. The equaliser matrix ![]() operates on the input as shown in Equation (13):
operates on the input as shown in Equation (13):
![]() (13)
(13)
with a system matrix![]() , where
, where![]() . The purpose of the binary matrix
. The purpose of the binary matrix ![]() is not only to act as a frequency guard band and help lower out- of-band emissions, but also to eliminate components that would appear in the upper right and lower left corners in
is not only to act as a frequency guard band and help lower out- of-band emissions, but also to eliminate components that would appear in the upper right and lower left corners in ![]() [23] . The estimated data vector is given by Equation (14):
[23] . The estimated data vector is given by Equation (14):
![]() (14)
(14)
where ![]() is the equaliser matrix. The equivalent
is the equaliser matrix. The equivalent ![]() subcarrier coupling matrix (frequency domain channel matrix) and the noise vector in the frequency domain are given by
subcarrier coupling matrix (frequency domain channel matrix) and the noise vector in the frequency domain are given by ![]() and
and ![]() respectively. It is straight forward to show that
respectively. It is straight forward to show that
![]()
![]() (15)
(15)
From Equation (9), it can be shown that ![]() appears on the main diagonal of
appears on the main diagonal of![]() ,
, ![]() on the first super-diagonal,
on the first super-diagonal, ![]() on the first sub-diagonal and
on the first sub-diagonal and
so on. This means that ![]() can be considered as the frequency-domain response, at subcarrier
can be considered as the frequency-domain response, at subcarrier![]() , to a frequency-domain impulse centred at subcarrier
, to a frequency-domain impulse centred at subcarrier![]() . In
. In![]() ,
, ![]() can be understood as Doppler index and
can be understood as Doppler index and ![]() as the as the frequency index. In
as the as the frequency index. In![]() ,
, ![]() can be interpreted as the time index and
can be interpreted as the time index and ![]() as the lag index.
as the lag index.
Now consider the DFrFT-OCDM system in Figure 3.
It is almost the same as the OFDM system except the modulation and demodulation blocks are replaced by the inverse fractional Fourier transform IDFrFT and the fractional Fourier transform DFrFT respectively. Applying the same procedure for the data
![]()
Figure 3. DFrFT-OCDM system block diagram.
to be transmitted in the transmitter and the receiver so it is straight forward to show that the equaliser matrix ![]() operates on the input as shown in Equation (16):
operates on the input as shown in Equation (16):
![]() (16)
(16)
where ![]() is the DFrFT,
is the DFrFT, ![]() is the IDFrFT,
is the IDFrFT, ![]() is the fractional angle in the fractional domain and
is the fractional angle in the fractional domain and ![]() is the system matrix with
is the system matrix with![]() . The equivalent
. The equivalent ![]() channel matrix
channel matrix ![]() and the noise vector
and the noise vector ![]() in the fractional domain are given by Equations (17) and (18)
in the fractional domain are given by Equations (17) and (18)
![]() (17)
(17)
![]() (18)
(18)
![]() and
and ![]() are non-diagonal subcarrier channel matrices introduce ICI, which is the case when the dispersive channel comprises a multipath doubly dispersive channel. This will make the symbol estimation task particularly complicated due to the need for complicated equaliser.
are non-diagonal subcarrier channel matrices introduce ICI, which is the case when the dispersive channel comprises a multipath doubly dispersive channel. This will make the symbol estimation task particularly complicated due to the need for complicated equaliser.
3. Study of Peak-to-Peak Average Power Ratio
One particular drawback of all multicarrier systems is their peak-to-average power ratio (PAPR) (large fluctuations in the transmitted signal envelop), which is higher than that of single-carrier UWB systems and pulsed-based UWB approaches. Large PAPR needs an expensive power amplifier with large linear region, and leads to increased complexity of the analog-to-digital and digital to-analog converters. Therefore, it is important to investigate the PAPR performance of the multicarrier systems.
The PAPR of the discrete transmit signal has been studied in [12] [18] [19] and given by Equation (19):
![]() (19)
(19)
where the numerator denotes the maximum instantaneous power and the denominator denotes the average power of the signal. The PAPR performance of a multicarrier system is evaluated in terms of the complementary cumulative distribution function (CCDF) of PAPR which denotes the probability that the PAPR of a data block exceeds a given threshold![]() , i.e.,
, i.e.,![]() .
.
In [24] a simple approximate expression is derived for the CCDF of the PAPR of a multicarrier signal with Nyquist rate sampling. From the central limit theorem, the real and imaginary parts of the time domain signal samples follow Gaussian distributions, each with a mean of zero and a variance of 0.5 for a multicarrier signal with a large number of subcarriers. Hence, the amplitude of a multicarrier signal has a Rayleigh distribution, while the power distribution becomes a central chi-square distribution with two degrees of freedom with a cumulative distribution given by Equation (20):
![]() (20)
(20)
To derive the CCDF for the peak power per OFDM symbol, assuming the samples are mutually uncorrelated which is true for non over sampling, the probability that the PAPR is below some threshold level ![]() can be written as Equation (21) and Equation (22):
can be written as Equation (21) and Equation (22):
![]() (21)
(21)
![]() (22)
(22)
Substituting Equation (20) in Equation (22):
![]() (23)
(23)
The above expression is independent of the DFrFT and DFrCT transform order ![]() only under the Gaussian assumption.
only under the Gaussian assumption.
3.1. PAPR Reduction Techniques
Different techniques were proposed for the PAPR reduction problem like clipping [25] [26] , coding [17] [27] [28] , and multiple signal representation techniques such as partial transmit sequence (PTS) [29] and selected mapping (SLM) [30] . These techniques reduce the PAPR with one or more overheads of transmit signal power increase, computational complexity increase, data rate loss and bit error rate (BER) increase.
1) Clipping
Amplitude clipping is the simplest technique for PAPR reduction as it limits the peak envelope of the input signal to a predetermined value as shown in Equation (24):
![]() (24)
(24)
where ![]() is the output of the clipping function and A is the clipping amplitude.
is the output of the clipping function and A is the clipping amplitude.
Clipping may be considered as a source of in-band and out of-band distortion. Filtering after clipping is proposed in [26] where the out of-band distortion can be reduced while the in-band distortion effect can be reduced in the receiver by iteratively reconstruct the signal before clipping [13] .
2) Coding
Reducing the PAPR may be visible by avoiding the transmission of certain sequences known to have large PAPR. However, this technique suffers from complexity limitations, as searching for the best codes and the storage of large lookup tables for encoding and decoding, especially for a large number of subcarriers. A more complex approach proposed in [28] was trying to benefit from different code-words by using its error correcting properties and to reduce the PAPR of the resulting coded signals. This approach is simple to implement, but it requires extensive calculations to find good codes. Golay complementary sequences with their attractive PAPR control properties and the classical first-order Reed-Muller code with all of the encoding, decoding, and error correcting capability were proposed in [27] .
The effectiveness of these coding techniques is limited for practical multicarrier systems PAPR reduction due to the exhaustive search needed for finding a good code which is a limitation for multicarrier systems with a small number of subcarriers.
3) The Selected Mapping Technique
In the selected mapping technique (SLM) [30] , the transmitter generates a number of different candidate data blocks which are equivalent to the original data block, and selects the one with the lowest PAPR for transmission. A block diagram for the SLM technique is shown in Figure 4. Each data block is multiplied by U different phase sequences, each of length equal to the data block length as shown in Equation (25):
![]() (25)
(25)
resulting in U adapted data blocks. B1 is set to be all one vector to include the original data block in our search. The adapted data block for the ![]() phase sequence will be as shown in Equation (26):
phase sequence will be as shown in Equation (26):
![]() (26)
(26)
after applying SLM to X, the multicarrier signal is given by Equation (27):
![]() (27)
(27)
The minimum PAPR is selected from the adapted data blocks to be transmitted. The receiver needs information about the selected independent vectors to ensure the correct recovery of the transmitted signals. These sequences should be transmitted to the receiver as side information. For implementation, the SLM technique needs U − 1 extra transformation operations, and the number of required side information bits is ![]() for each data block. This approach is applicable to all types of modulation and any number of subcarriers.
for each data block. This approach is applicable to all types of modulation and any number of subcarriers.
Selecting the frame with the lowest PAPR for transmission from U statistically independent OFDM frames represent the same information. The probability that PAPR min exceeds ![]() using Equation (23) is given by Equation (28) and Equation (29):
using Equation (23) is given by Equation (28) and Equation (29):
![]() (28)
(28)
![]() (29)
(29)
![]()
Figure 4. A block diagram of the SLM technique.
From Equation (17), the amount of PAPR reduction for SLM depends on the number of phase sequences U and the design of the phase sequences. PAPR reduction is possible for all data blocks but it may vary from one to one.
4) The Partial Transmit Sequence Technique
In the partial transmit sequence (PTS) approach [29] , the input data block is partitioned into multi disjoint sub-blocks or clusters. The subcarriers in each sub-block are weighted by carefully choosing a phase factor for that sub-block in such a way that minimizes the PAPR of the combined signal. Generally, three methods of partition have been provided: adjacent partition, pseudo-random partition and interleaved partition.
The block diagram of the PTS technique is shown in Figure 5. The input data block
X is partitioned into K disjoint sub-blocks ![]()
such that![]() , the time domain signal
, the time domain signal ![]() is obtained after the transformation of each one of the portioned signals
is obtained after the transformation of each one of the portioned signals ![]() (each one is completed by zero padding) and denoted
(each one is completed by zero padding) and denoted ![]() these time domain signals are called the partial transmit sequences. These PTSs are combined with different complex phase factors from the set denoted by
these time domain signals are called the partial transmit sequences. These PTSs are combined with different complex phase factors from the set denoted by![]() .
.
The main task is to find the set of phase factors that minimizes the PAPR. To reduce the search complexity for the best phase factors a limited finite number of elements are defined by Equation (30):
![]() (30)
(30)
where W is the number of allowed phase factors. It is clear that the search complexity increases exponentially with the number of sub-blocks K.
It is obvious, that the receiver must have knowledge about the generation process of the transmitted signal and the phase factors used so that the subcarriers can be rotated back appropriately. The number of bits required to represent this side information is the amount of redundancy introduced by the PAPR reduction scheme with PTS. Note that the number of the redundancy bits for the PTS technique is less than that needed for the SLM technique.
The amount of PAPR reduction depends on the number of sub-blocks K and the number of allowed phase factors W. Another factor that may affect the PAPR reduction
performance in PTS is the sub-block partitioning method. The PTS technique works with an arbitrary number of subcarriers and any modulation scheme.
3.2. Selection of PAPR Reduction Technique
Choosing one of the previously discussed PAPR techniques depends on many factors which bring up subsequent costs for PAPR reduction. These factors and costs include computational complexity increase, lower PAPR reduction capability, power increase for signal transmission, BER increase at the receiver and losses in data rate.
Due to these factors the choice of the best PAPR candidate technique depends on the multicarrier system application.
3.3. Multicarrier Systems Based on Different Unitary Transformation Matrices Comparison under Doubly Selective Fading Channel Scenario
Multicarrier Modulation (MCM) systems popularity started after the use of Fourier transformation as the modulation/demodulation technique in many wired and wireless communication standards. The idea is to adopt a unitary transformation basis as the basis for the MCM system which reduces the modulation and demodulation complexity [21] [31] [32] .
Comparing the performance of the different transformations used as basis for the MCM system under the doubly dispersive channel scenario will give a good vision for the developers of the new techniques under the great demand on mobile data communication and green devices.
It is straight forward to identify a general MCM system block diagram from OFDM system, DFrFT-OCDM system and DFrCT-OCDM system and hence deduce the equation that can specify the estimated data vector in the receiver for all the previously listed transformation based MCM systems which can be found in [33] .
In this paper, we use the simulation results to compare the performance of the different transformations system used as basis for the MCM system.
A BER performance comparison between OFDM, Discrete Cosine Transform MCM (DCT-MCM), Discrete Hartley Transform MCM (DHT-MCM), DFrFT-OC0DM and DFrCT-OCDM MCM systems was done by means of simulation over 100000 multicarrier blocks for each one.
4. Simulation Results
To evaluate the performance of the previous sections, computer simulations are established.
DFrCT-OCDM PAPR performance is measured without using any PAPR reduction methods using QPSK and 32, 64 and 128 subcarriers modulation and fractional order a = 0.25, U = 4 with 106 blocks of data generated.
Figure 4 shows that using DFrCT or DFrFT as a basis for the multicarrier system reduces the PAPR, which confirms the analytical approximation given by Equation (23). Moreover, Increasing the number of subcarriers limits the PAPR reduction gained by the DFrFT and the DFrCT.A DFrFT-OCDM system can reduce the PAPR more efficiently than the DFrCT-OCDM system as shown in Figure 6(a).
Same behaviours are repeated in all Figure 6(a), Figure 4(b), and Figure 4(c) when changing N, i.e., The PAPR decreases when increasing N, which is clearly justified by decreasing the time interval for each subcarrier, moreover, the rate that N changes decreases when N increases, for example, when changing N from 32 to 64, ![]() (dB) changes from 10.8 dB to 11.5 dB (different of 0.8 dB) in DFrCT, 9.9 dB to 11.1 dB (deferent of 1.2 dB) in DFrFT and 11.5 dB to 12.0 dB (different of 0.5 dB) in FFT comported to 0.3 dB, 0.5 dB, and 0.1 dB) for DFrCT, DFrFT and FFT respectively when changing N from 64 to 128. Finally in Figure 4, it is clear that FFT is the less scenario regarding changing N, and then DFrCT, and then DFrFT which is justified by using more fractional values in DFrCT than FFT and in DFrFTtahn FFT.
(dB) changes from 10.8 dB to 11.5 dB (different of 0.8 dB) in DFrCT, 9.9 dB to 11.1 dB (deferent of 1.2 dB) in DFrFT and 11.5 dB to 12.0 dB (different of 0.5 dB) in FFT comported to 0.3 dB, 0.5 dB, and 0.1 dB) for DFrCT, DFrFT and FFT respectively when changing N from 64 to 128. Finally in Figure 4, it is clear that FFT is the less scenario regarding changing N, and then DFrCT, and then DFrFT which is justified by using more fractional values in DFrCT than FFT and in DFrFTtahn FFT.
Figure 7 shows that different values of fractional order a can change the PAPR of the multicarrier system. Very small values of a can convert the system from a multicarrier system to a single carrier one which has a very small PAPR compared to multicarrier systems, however, increasing a results to increasing ![]() (dB) which is justified by the reason of the more a increases the more the system behaves differently from the single carrier when a ideally is equal to zero.
(dB) which is justified by the reason of the more a increases the more the system behaves differently from the single carrier when a ideally is equal to zero.
SLM can be considered as one of the best PAPR reduction techniques as it is an efficient and low complexity technique. The PAPR performance of the DFrCT-OCDM system using the SLM reduction technique is shown in Figure 6.
From Figure 8, SLM PAPR reduction technique reduces the PAPR for the DFrCT- OCDM, DFrFT-OCDM and the OFDM systems almost by the same ratio which indicates that the PAPR reduction methods can work efficiently with the DFrCT-OCDM, which confirms the theoretical framework of Equation (29), moreover, the performance of SLAM is justified by the mapping selective privilege that this technique provides. Improving the mapping selective technique is one of the proposed future work.
Figure 8 illustrates that there is improvement in ![]() (dB) from (10 dB to 12 dB) for all techniques when SLAM is not implemented to (5.5 dB to 6 dB) for all techniques when SLAM in implemented. Moreover, the deferent between all proposed techniques is much smaller when applying SLAM technique which is justified by the amount of improvement in the system itself and the benefit gained by SLAM. Based on Figure 6, we can confirm that SLAM technique fits all systems almost similarly which gives this technique the good reputation it deserves.
(dB) from (10 dB to 12 dB) for all techniques when SLAM is not implemented to (5.5 dB to 6 dB) for all techniques when SLAM in implemented. Moreover, the deferent between all proposed techniques is much smaller when applying SLAM technique which is justified by the amount of improvement in the system itself and the benefit gained by SLAM. Based on Figure 6, we can confirm that SLAM technique fits all systems almost similarly which gives this technique the good reputation it deserves.
The BER performance comparison between OFDM, DCT-MCM, DHT-MCM, DFrFT- OCDM and DFrCT-OCDM MCM systems is shown in Figure 9 by means of simulation over 100,000 multicarrier blocks for each system. A general MCM system with N = 128, NA = 96, L = 8, and QPSK modulation is assumed. The doubly dispersive channel simulation parameters are the same as the Rayleigh fading channel used for the results obtained above, and the MMSE equaliser was used to compensate the doubly dispersive channel distortion as shown in Figure 8.
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 6. PAPR performance of DFrCT-OCDM, DFrFT-OCDM and the OFDM system without PAPR reduction with QPSK at sub-carriers, a = 0.25, and the number of sub-carriers (a) N = 32, a = 0.25; (b) N = 64, a = 0.25; and (c) N = 128, a = 0.25.
![]()
Figure 7. PAPR performance of DFrCT-OCDM and OFDM systems without PAPR reduction at a = 0.2 and 0.5 with N = 32.
![]()
Figure 8. PAPR reduction performance of DFrCT-OCDM, DFrFT-OCDM and the OFDM systems with and without SLM-PAPR reduction.
![]()
Figure 9. The BER performance comparison between OFDM, DCT-MCM, DHT-MCM, DFrFT- OCDM and DFrCT-OCDM; MCM systems using MMSE equalize.
The fractional based MCM systems can deal well with the doubly dispersive channels as its chirp basis can cope with the channel frequency variations. The DFrCT-OCDM system gives the best performance due to its basis frequency components variation which is higher than the rest of the other scenarios
5. Conclusions
In this paper, we studied the PAPR performance of multicarrier systems based on the DFrCT, which are more robust multicarrier systems under doubly dispersive fading channels with respect to the traditional OFDM and the DFrFT-OCDM systems. Theoretical as well as simulation results suggest that the DFrCT-OCDM system outperforms OFDM system. However, for a large value of sub-carriers, both systems become equivalent. Furthermore, introducing the conventional methods of PAPR reduction into the fractional domain shows that it is possible to extend techniques developed for OFDM system (such as SLM technique) to DFrCT-OCDM systems.
Finally a comparison between the multicarrier systems based on different unitary transformation matrices comparison under doubly selective fading channel scenario was introduced and the DFrCT-OCDM system found to give the best performance.
In future work, the author plans to apply the principle of network coding over the erasure channel described in [34] and over the physical layer following work presented in [35] . Moreover, proposing power efficient protocols for the proposed system is an idea also included in plans for future work.
One more important direction in the future plans is to improve the Selected Mapping Technique (SLM) by improving the selective matrix before choosing the minimum PAPR.
Acknowledgements
Philadelphia University deserves my true acknowledgements for the good atmosphere they maintain for their researchers and for the financial support for this research.
Moreover, I am always thankful for Dr. Lina Stankovic and Dr. Vladimir Stakovic from the University of Strathclyde, Glasgow, UK, for their support with the technical issues, beside their proof reading and technical modifications in my whole research work. They always add good values for my research work.