1. Introduction
The author finds that the supposition as to the inevitability of low frequency Gravitational waves from the big bang is supported only by the conclusion that large spatial dimensions above our four dimensions are conduits as to dumping cyclical universe matter-energy into. The initial smallness of the higher dimensions was the reason why Brustein, Giovanni and others as of (1995) [1] wrote well received string theory articles predicting no favoring of low frequency gravitational waves (GW) as the primary relic Gravitational waves signature from the big bang which has been further updated in [2] . Doing so, also, will lead to another item repeatedly not faced by current physics research. Facing up to if initial generations of Gravitational Waves/gravity are due to either classical processes, in highly nonlinear subsequent evolution, or if the processes must be quantum [3] . And how much squeezing of states in initial conditions for inflation (super inflation in the loop quantum gravity (LQG)) scenario is listed by no less that Bojowald (2008) [4] as an open problem, which will be brought up toward the end of this document, as part of what Beckwith views as important future goals as to cosmology research. The relative role of classical processes in initial vacuum states from emergent fields, versus quantum has implications far beyond the initial spectrum of GW from relic conditions.
First though we will clarify an issue brought up by a referee, whom assumed that there was a conflict between the Glinka [5] quantum gas and the idea of infinite quantum statistics, as given by Ng [6] . We will be referring to this in passing.
Note a point, brought up by the referee, i.e. that
Quote (From the referee)
Ng’s result is being considered on a scale R_H. First of all, it is not clear what R_H is. Is it the Hubble or horizon scale during inflation? If this is the case, it would not be unexpected that Ng's and Glinka’s results might match.
End of quote
The author is happy to report that the referee’s suggestion about the Horizon scale is correct. See also the extensive discussion put in, as far as the startling effects of relativistic speeds for the massive gravitons and due to the existence of massive gravity, that there is, due to extreme initial speeds of the massive gravitons, a full equivalence between the Glinka [5] and Ng [6] results.
2. Comparison of the Interconnections between Glinka’s Graviton Gas, and Ng’s Infinite Quantum Statistics
As brought up by a referee, there appears at first glance to be a potential conflict between the idea of the Infinite quantum statistics, of Ng [6] , which was proposed for dark matter, and the idea of quantum gas treatment of gravitons which is Glinka’s suggestion [5] . What the author is suggesting is that the idea of using a particle count algorithm along the lines of Ng [6] with gravitons, will be still using the following equation given as to wave length of a graviton, connected with mass, i.e. from Valev [7]
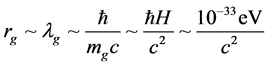 (1)
(1)
The left hand side of this is, of course, a quantum process, whereas the right hand side with H, Hubble parameter, is clearly semi-classical. i.e. we are seeing an equivalence between these values.
Secondly, according to the simple special relativistic formula of the value given by Jackson [8]
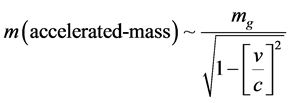 (2)
(2)
For the accelerated mass of a 10−33 eV rest graviton mass to have a special relativistic mass of at least 1 electron volt, the velocity of the graviton would be of the order of
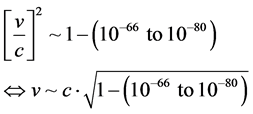 (3)
(3)
This means that if the velocity of a rest graviton mass were of the order of what is given in Equation (3), that then the effective mass of a graviton would be at least one electron volt, to a Giga volt.
Now comparing this to Dark matter, i.e. we can look at what was given by E. Kolb and M. Turner, [9] i.e. that Axions can range in value up to say 1 electron volt, and that other Dark matter candidates can range in value up to over 10 - 100 Giga volts, that the values in Equation (3) are commensurate with at least an accelerated version of gravitons having the mass of Axions, up to some of the other more conventional WIMP dark matter candidates.
Recall if you will that Ng [10] have it that there would be a wavelength, as part of the derivation of entropy included in the entropy formula of
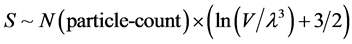 (4)
(4)
The answer, as given by Ng, is that if the volume of space, V, is-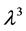 , and that
, and that 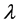 is proportional to the wavelength associated with Dark matter, according to Equation 1 above, then due to the situation of how a massive graviton could at least have accelerated mass values on par with dark matter candidates, this will allow for the Ng formula, being changed to
is proportional to the wavelength associated with Dark matter, according to Equation 1 above, then due to the situation of how a massive graviton could at least have accelerated mass values on par with dark matter candidates, this will allow for the Ng formula, being changed to
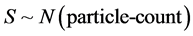 (5)
(5)
allegedly for DM, to be relevant for massive gravitons traveling at near the speed of light. Note that the result given in Equation (3) above, is, as noted by Ng [10] a duplication of a string theory result. We will be stating that this is commensurate with the quantum based graviton gas interpretation of Glinka [5] provided that the gravitons, are, indeed massive, and that they are accelerated at nearly the speed of light, with a velocity similar to what is given in Equation (3) above.
This connection between the Glinka result for a graviton gas (provided it is for massive gravitons which are traveling at almost the speed of light), with its quantum overturns, as seen in [5] when combined with our use of the Dark matter results of Ng [10] for infinite quantum statistics, as given in Equations (4) and Equations (5) will provide the conceptual underpinnings of what we are talking about, next.
3. What about the Inter Relation of String Theory with Counting Algorithms for DM and Graviton Production, in Terms of Entropy?
So, what can be said about the Y. J. Ng paradigm of entropy generation [10] , which Beckwith has modified and looked at? For a start, consider if the counting algorithm, which is a string theory result, can have any common results with a quantum gas result, which comes from the Wheeler de Witt (WDW) equation, whose solution is WKB, semi-classical in nature? If there is a close inter connection between the classical and quantum formalisms, with the quantum formulation being close to classical values, we are observing many coherent states, indicating
The question of relative over lap of classical and quantum processes in terms of wave functions for the evolution of the universe will be crucially important in determining coherency issues as far as relic GW, and gravitons from relic conditions, which the author will return to repeatedly during this presentation.
4. Example of the Inter Connection between Semi Classical and Quantum Processes, as Exemplified by the Schrodinger Equation and Its Semi-Classical Representations
As given by M. Hall and M. Reginatto [3] , we have that on pages 105-107, of [3] .
We have that by application of what is called an exact Uncertainty principle, with, i.e. a situation where there is a way to derive a Schrodinger equation, from starting off with ³ in the Heisenberg uncertainty principle, replaced by an equality, to have the reduced Hamilton Jacobi gravity equation Hamiltonian 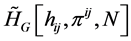 as given by
as given by
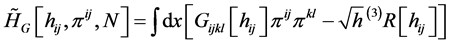 (6)
(6)
As the gravitational field version of the Hamilton-Jacobi Equation, given by [11] and [12] .
This Equation (6) has a semi-classical form and using the exact form of the Heisenberg Uncertainty principle, will lead to a functional form of the Schrodinger Equation given as
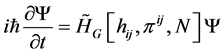 (7)
(7)
This Equation (7) is a direct result of applying the result given in Hall and Reginatto [3] , page 98, as to momentum field density, and classical field as a Hamilton Jacobi equation in ways in conjunction with the “exact Heisenberg uncertainty Principle” in order to get the Functional quantum Schrodinger equation given in Equation (7). i.e. we claim that the inter relationship.
The basis of this discussion is that what is called using the Hamilton-Jacobi equation restricted above (which is semi-classical) in order to go to quantum results, and that due to a severely modified Heisenberg Uncertainty principle, with the ³ replaced by an equality =.
This is an analogy as to how we are linking the semi-classical Glinka graviton gas, as given in [5] with the quantum (string theory!) results derived by Ng [6] [10] , and that also by the device we have shown earlier as to how massive gravitons may, if traveling close to the speed of light have an effective mass equivalent to the dark matter which was used in the infinite quantum statistics work of Ng [10] . Having said that, let us go to the next chapter of our review.
5. Review of Simple Models as to Gravitons as Produced Either by (Quantum Gravity) Strings, or Some Form of LQG
We wish now to review what may be some of the counting algorithms appropriate for entropy generation, and which may contribute to answering if or not GW are mandated to be, from the beginning either a classical versus a quantum processes. IN part this next page is due to concepts A. Beckwith presented in Rencontres De Blois, 2009 [13] , and is a starting point for our inquiry as to the necessity, or lack of, of modeling Gravity as either classical/quantum based in relic conditions.
6. Introduction to Infinite Quantum Statistics
1) Is each “particle count unit” as suggested by Ng equivalent to a brane-antibrane unit in brane treatments of entropy?
2) Is the change of entropy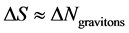 ?
?
3) Is this graviton production scheme comparable to Glinka’s quantum gas, from the Wheeler De Witt equation?
7. Entropy Generation via Ng’s Infinite Quantum Statistics
This discussion is motivated to show a purely string theory approach and to see if its predictions may overlap with semi-classical WDM [3] [9] (semi-classical) treatments of cosmology. The contention being advanced is that if there is an overlap between these two methods that it may aid in obtaining experimentally falsifiable data sets for GW from relic conditions.
We wish to understand the linkage between dark matter and gravitons. How relic gravitational waves relate to relic gravitons”? To consider just that [6] [10] , we look at the “size” of the nucleation space, V for dark matter, DM. V for nucleation is HUGE. Graviton space V for nucleation is tiny, well inside inflation. Therefore, the log factor drops OUT of entropy S if V chosen properly for both Equation (1) and Equation (2). Ng’s result begins with a modification of the entropy/partition function Ng used the following approximation of temperature and its variation with respect to a spatial parameter, starting with temperature 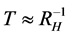 (
(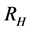 can be thought of as a representation of the region of space where we take statistics of the particles in question). Furthermore, assume that the volume of space to be analyzed is of the form
can be thought of as a representation of the region of space where we take statistics of the particles in question). Furthermore, assume that the volume of space to be analyzed is of the form 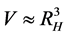 and look at a preliminary numerical factor we shall call
and look at a preliminary numerical factor we shall call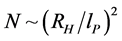 , where the denominator is Planck’s length (on the order of
, where the denominator is Planck’s length (on the order of 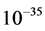 centimeters). We also specify a “wavelength” parameter
centimeters). We also specify a “wavelength” parameter . So the value of
. So the value of 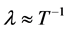 and of
and of ![]() are approximately the same order of magnitude. Now this is how Jack Ng changes conventional statistics: he outlines how to get
are approximately the same order of magnitude. Now this is how Jack Ng changes conventional statistics: he outlines how to get![]() , which with additional arguments we refine to be
, which with additional arguments we refine to be ![]() (where
(where ![]() is graviton density). Begin with a partition function [6] [10]
is graviton density). Begin with a partition function [6] [10]
![]() (8)
(8)
This, according to Ng, [6] [10] , leads to entropy of the limiting value of, if
![]() (9)
(9)
But![]() , so unless N in Equation (9) above is about 1, S (entropy) would be <0, which is a contradiction. Now this is where Jack Ng [6] [10] introduces removing the N! term in Equation (8) above, i.e., inside the Log expression we remove the expression of N in Equation (9) above. The modification of Ng’s entropy expression is in the region of space time for which the general temperature dependent entropy Kolb and Turner [9] expression breaks down. In particular, the evaluation of entropy we do via the modified Ng argument above is in regions of space time where g before re heat is an unknown, unmeasurable number of degrees of freedom The Kolb and Turner entropy expression (1991) [9] has a temperature T related entropy density which leads to that we are able to state total entropy as the entropy density time’s space time volume
, so unless N in Equation (9) above is about 1, S (entropy) would be <0, which is a contradiction. Now this is where Jack Ng [6] [10] introduces removing the N! term in Equation (8) above, i.e., inside the Log expression we remove the expression of N in Equation (9) above. The modification of Ng’s entropy expression is in the region of space time for which the general temperature dependent entropy Kolb and Turner [9] expression breaks down. In particular, the evaluation of entropy we do via the modified Ng argument above is in regions of space time where g before re heat is an unknown, unmeasurable number of degrees of freedom The Kolb and Turner entropy expression (1991) [9] has a temperature T related entropy density which leads to that we are able to state total entropy as the entropy density time’s space time volume ![]() with
with![]() , according to De Vega [14] , while dropping to
, according to De Vega [14] , while dropping to ![]() in the electro weak era. This value of the space time degrees of freedom, according to de Vega [14] has reached a low of
in the electro weak era. This value of the space time degrees of freedom, according to de Vega [14] has reached a low of ![]() today. We assert that Equation (9) above occurs in a region of space time before
today. We assert that Equation (9) above occurs in a region of space time before![]() , so after re heating Equation (9) no longer holds, and we instead can look at [9]
, so after re heating Equation (9) no longer holds, and we instead can look at [9]
![]() (10)
(10)
where![]() . We can compare Equation (8) and Equation (9), as how they stack up with Glinka’s (2007) quantum gas [5] , if we identify
. We can compare Equation (8) and Equation (9), as how they stack up with Glinka’s (2007) quantum gas [5] , if we identify ![]() as a partition
as a partition
function (with u part of a Bogoliubov transformation) due to a graviton-quintessence gas, to get information theory based entropy
![]() (11)
(11)
Such a linkage would open up the possibility that the density of primordial gravitational waves could be examined, and linked to modeling gravity as an effective theory. The details of linking what is done with Equation (8) and bridging it to Equation (9) await additional theoretical development, and are probably conceptually understandable if the following is used to link the two regimes. i.e. we can use the number of space time operations used to create Equation (8) via Seth Lloyds [15]
![]() (12)
(12)
Essentially, what will be done is to use Equation (12) to show linkage between a largely thermally based production of entropy, as implied by Equation (10) and a particle counting algorithm, as given by Equation (2). This due to the problems inherent in making connections between a particle count generation of entropy, and thermal contributions. i.e. two different processes are involved. The big news is though that the WKB is semi-classical, whereas anything from string theory is, well, QFT, plus.
Where there is an overlap between a classical wave function, and its quantum mechanical analog, that means there is a minimization of spreading of a wave functional. i.e. see Roy Glauber (1963) [16] .
One can say the following. That if there is an overlap between the Wheeler De Witt equation derived quantum gas which was brought up by Glinka (2007) [5] , where the WDW can have WKB semi-classical solutions, and we are using the string theory counting algorithm, Then, if the end results are similar, the fact is that the quantum procedure, i.e. Brane theory, is over lapping with WKB, means that there is a minimization of uncertainty. Note that the supposition of how classical and quantum processes can give similar answers is presented in rich detail by Roy Glauber (1963) [16] and the example talked about here is its GW analog.
Gravitons are stated conceptually to be akin to photons in light waves. If there is a large deviation/perturbation of the initially Gaussian states of space time wave functions, there is likely a break from classical physics due to the complexity of evolving wave function states influenced increasingly by non Gaussian perturbations. This non Gaussian process is reflected by marked deviation from planar wave state approximations used in the evolution of wave functions.
In the case of gravitons, as coherent states, once squeezing of coherent states occurs, the, mere act of squeezing of the initial states destroys the initial classical super position of graviton states which would contribute to a GW. How and what particular mix of squeezed versus un squeezed relic states one can expect is important for determining frequencies to look for which are from relic conditions. Relic GW are messy, and the most dominant/important frequencies identified can if properly analyzed confirm/ falsify many of our early universe cosmology theories as far as relic conditions. How does one actually know about first or second order phase transitions, due to GW. Since it has been brought up, let us now review, briefly the issue of coherence, versus de coherence of initial vacuum states, and its relevance as to classical versus quantum factors as to generation of GWs.
8. Issues about Coherent State of Gravitons (Linking Gravitons with GW)
In the quantum theory of light (quantum electrodynamics) and other bosonicquantum field theories, coherent states were introduced by the work of Roy J. Glauber [16] in 1963 Now, it is well appreciated that Gravitons are NOT similar to light. Coherent states, to first approximation are retrievable as minimum uncertainty states. If one takes string theory as a reference, the minimum value of uncertainty becomes part of a minimum uncertainty which can be written as given by Gasperni, and Venziano (1993) [17] , where![]() , with
, with![]() , and
, and ![]() centimeters
centimeters
![]() (13)
(13)
This is furthermore elaborated upon in [18] .
To put it mildly, if we are looking at a solution to minimize graviton position uncertainty, we will likely be out of luck if string theory is the only tool we have for early universe conditions. Mainly, the momentum will not be small, and uncertainty in momentum will not be small either. Either way, most likely, ![]() In addition, it is likely, as Klaus Kieffer in the book “Quantum Gravity” [19] on page 290 of that book that if gravitons are excitations of closed strings, then one will have to look for conditions for which a coherent state of gravitons, as stated by Mohaupt (2003) occurs [20] . What Mohaupt [20] is referring to is a string theory way to re produce what Ford gave in 1995 [21] , i.e. conditions for how Gravitons in a squeezed vacuum state, the natural result of quantum creation in the early universe will introduce metric fluctuations. Ford’s (1995) [21] treatment is to have a metric averaged retarded Green's function for a massless field becoming a Gaussian. The condition of Gaussianity is how to obtain semi-classical, minimal uncertainty wave states, in this case de rigor for coherent wave function states to form. Ford uses gravitons in a so called ‘squeezed vacuum state’ as a natural template for relic gravitons. i.e. the squeezed vacuum state (a squeezed coherent state) is any state such that the uncertainty principle is saturated. In QM coherence would be when
In addition, it is likely, as Klaus Kieffer in the book “Quantum Gravity” [19] on page 290 of that book that if gravitons are excitations of closed strings, then one will have to look for conditions for which a coherent state of gravitons, as stated by Mohaupt (2003) occurs [20] . What Mohaupt [20] is referring to is a string theory way to re produce what Ford gave in 1995 [21] , i.e. conditions for how Gravitons in a squeezed vacuum state, the natural result of quantum creation in the early universe will introduce metric fluctuations. Ford’s (1995) [21] treatment is to have a metric averaged retarded Green's function for a massless field becoming a Gaussian. The condition of Gaussianity is how to obtain semi-classical, minimal uncertainty wave states, in this case de rigor for coherent wave function states to form. Ford uses gravitons in a so called ‘squeezed vacuum state’ as a natural template for relic gravitons. i.e. the squeezed vacuum state (a squeezed coherent state) is any state such that the uncertainty principle is saturated. In QM coherence would be when![]() . In the case of string theory it would have to be
. In the case of string theory it would have to be
![]() (14)
(14)
Begin with noting that if one is not using string theory, we merely set the term![]() , but that we are still considering Roy Glauber (1963) [16] with string theory replacing his stated example.
, but that we are still considering Roy Glauber (1963) [16] with string theory replacing his stated example.
However, what one sees in string theory, is a situation where a vacuum state as a template for graviton nucleation is built out of an initial vacuum state,![]() . To do this though, as Venkatartnam, and Suresh [22] did, involved using a squeezing operator
. To do this though, as Venkatartnam, and Suresh [22] did, involved using a squeezing operator ![]() defining via use of a squeezing parameter r as a strength of squeezing interaction term, with
defining via use of a squeezing parameter r as a strength of squeezing interaction term, with![]() , and also an angle of squeezing,
, and also an angle of squeezing, ![]() as used in
as used in
![]()
where combining the ![]() with
with
![]() (15)
(15)
Equation (15) leads to a single mode squeezed coherent state, as they define it via
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
If ![]() is picked, and a Schrodinger equation is made out of the Lagrangian used to formulate Equation (18) above, with
is picked, and a Schrodinger equation is made out of the Lagrangian used to formulate Equation (18) above, with
![]() (19)
(19)
And
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
and ![]() an arbitrary function.
an arbitrary function.![]() . Also, we have a finite volume
. Also, we have a finite volume
![]() (23)
(23)
Then the Lagrangian for deriving Equation (18) is (and leads to a Hamiltonian which can be also derived from the Wheeler De Witt equation), with ![]() for zero point subtraction of energy
for zero point subtraction of energy
![]() (24)
(24)
![]() (25)
(25)
Then there are two possible solutions to the S.E. Grishchuk created in 1989 and later, [24] [25] , one a non squeezed state, and another a squeezed state. So in general we work with
![]() (26)
(26)
The non squeezed state has a parameter ![]() where
where ![]() is an initial time, for which the Hamiltonian given in Equation (26) in terms of raising/ lowering operators is “diagonal”, and then the rest of the time for
is an initial time, for which the Hamiltonian given in Equation (26) in terms of raising/ lowering operators is “diagonal”, and then the rest of the time for![]() , the squeezed state for
, the squeezed state for ![]() is given via a parameter B for squeezing which when looking at a squeeze parameter r, for which
is given via a parameter B for squeezing which when looking at a squeeze parameter r, for which![]() , then (27) has, instead of
, then (27) has, instead of ![]()
![]() (27)
(27)
Taking Grishchuck’s formalism [24] [25] literally, a state for a graviton/ GW is not affected by squeezing when we are looking at an initial frequency, so that ![]() initially corresponds to a non squeezed state which may have coherence, but then right afterwards, if
initially corresponds to a non squeezed state which may have coherence, but then right afterwards, if ![]() which appears to occur whenever the time evolution
which appears to occur whenever the time evolution
![]() (28)
(28)
A reasonable research task would be to determine, whether or not ![]()
would correspond to a vacuum state being initially formed right after the point of nucleation, with ![]() at time
at time ![]() with an initial cosmological time some order of magnitude of a Planck interval of time
with an initial cosmological time some order of magnitude of a Planck interval of time ![]() seconds.
seconds.
9. Turbulence in Initial GW Production and How to Model It Classically or Quantum Mechanically
First of all it is relevant to note that the phenomenology in this section was largely given an experimental input basis as far as an experimentally doable set of measurements in [28] [29] . We are elaborating upon some of the issues as far as turbulence in the subsequent commentary.
What happens if there is a switch over from an initially uncompressed state, to one which has compression? Several things could happen. First of all, one may be able to see colliding plane wave representations of GW, i.e. the geometry of the colliding wave space time becomes amendable to analysis, as was presented by Vladimir Belinski, and Enric Venrauger [30] (2001) in their book on Gravitational solitons, starting on page 202. In particular, their Equation (7.60) has parameters which represent gravitational shock waves in collision, followed by trailing gravitational radiation. If one believes that relic GW processes can be largely preserved in the onset of the big bang in a “frozen” profile then the interactive region for generation of GW signals from GW shock waves in collision could account for the datum represented by Fangyu Li et al. (2009) [29] as far as the alleged random back ground as far as GW processes.
As Bojowald [31] (2008) wrote it up, in both his Equation (26) which has a quantum Hamiltonian![]() , with
, with
![]() (29)
(29)
and ![]() is a “volume” operator where the “volume” is set as V, Note also, that Bojowald has, in his initial Friedman equation, density values
is a “volume” operator where the “volume” is set as V, Note also, that Bojowald has, in his initial Friedman equation, density values![]() , so that when
, so that when
the Friedman equation is quantized, with an initial internal time given by![]() , with
, with ![]() becoming a more general evolution of state variable than “internal time”. If so, Bojowald [31] (2008) writes, when there are squeezed states
becoming a more general evolution of state variable than “internal time”. If so, Bojowald [31] (2008) writes, when there are squeezed states
![]() (30)
(30)
For his Equation (26), which is incidentally when links to classical behavior break down, and when the bounce from a universe contracting goes to an expanding present universe. Bojowald also writes that if one is looking at an isotropic universe, which as the large matter “H” increases, that in certain cases, one observes more classical behavior, and a reduction in the strength of a quantum bounce. Bojowalds states that “Especially the role of squeezed states is highlighted”.
I claim that what Bojowald [31] (2008) is leading up to, is specifying a parameter space in initial conditions which one may be able to do a semi-classical analysis of the sort referenced by Vladimir Belinski, and Enric Venrauger [30] (2001) in their book on Gravitational solitons, starting on page 202 of their text.. As stated earlier, their Equation (7.60) has parameters which represent gravitational shock waves in collision, followed by trailing gravitational radiation. Not only that, but initial un squeezed states may be, in part represented/presentable as due to the worm hole analysis of initially introduced from a prior universe, to today’s universe by the Wheeler De Witt pseudo time representation of an initial vacuum state, as has been brought up by Beckwith, in [32] [33] [34] [35] .
Last, but not least, would be to also examine, from first principles, what Christian Corda [36] [37] [38] raised as a distinct possibility Namely using “investigation of the transverse effect of gravitational waves (GW’s) could constitute a further tool to discriminate among several relativistic theories of gravity on the ground”. i.e. using transverse effects as another further tool to distinguish on the foundations of what Li et al. (2009) [29] listed as random background for the processes in which relic GW are generate in early space time conditions.
10. Conclusion: Time to Re Set Gravitational Wave Physics to Empirical Foundations
The final pay of re-setting the discussion back to laboratory science, will be in investigating a supposition t’Hooft advanced as to Quantum mechanics, which has never been satisfactorily investigated. The reconstruction of generation of GW in initial conditions may be allowing us to illustrate ‘t Hooft’s proposal to reconstruct quantum mechanics [39] as an emergent theory. The author, Beckwith, will in a subsequent publication, elaborate upon why early generation of GW could be the template as to investigating T’Hoofs supposition in proper detail, and what that could mean with respect to physics.
Secondly, Arkani-Hamed and other researchers, in [40] have posited the existence of “large” higher dimensions, as a way to obtain a small cosmological constant. However, their methodology, if closely follows makes gravity, and gravitational waves abysmally weak, as has been in [41] . i.e. this issue as to the strength of initial gravity, and gravitational waves needs to be gotten to the bottom of Aside from investigating foundational theories of gravity, as mentioned in the text, the Calabi Yau hypothesis, should be either falsified or confirmed, if possible, [42] . And of course this should be done in fidelity with the known properties of gravitation as given by the LIGO discovery [43] .
The potentiality of this investigating the issues brought up in [44] should not be minimized, as to changing our methodology of the formulation of the Heisenberg uncertainty principle, and it should be, in early universe conditions compared to the author’s work given in [45] , as well.
The issues so brought up may be partly explained by the work given in [46] , or well may not be, and this means some real experimental investigations, and looking at the roots of the quantum gravity problem, not adhering to post modern physics.
We bring up, also, an important issue, that not all cosmological models start expansion via the initial space-time singularity. The reference by [47] does not and neither does work just published by P.K. Sahoo, B. Mishra, Parbati Sahoo and S.K.J. Pacif [48] .
Quote
In this work we have studied Bianchi-III and -VI0 cosmological models with string fluid source in f(R, T) gravity (T. Harko et al., Phys. Rev. D 84, 024020 (2011)), where R is the Ricci scalar and T the trace of the stress energy-momentum tensor in the context of late time accelerating expansion of the universe as suggested by the present observations.
Quote
The universe is anisotropic and free from initial singularity.
String fluids, for those whom wish to know are a way to have (n + 1) dimensions, i.e. perhaps a nod to the Arkani Hamid picture, of extra dimensions, which may or may not be large, and [49] does give us that, as a starting point. But [49] does not necessarily do away with the initial space-time singularity. The importance of if there is an initial singularity can be seen in the question posed in the beginning about if there is a temporary un squeezed, possibly even coherent initial value, which would permit in certain models classical coherent initial gravitational wave states. Likely there would not be, if an initial singularity did not exist, and this is maintained, even if we look at [50] , i.e. this is one of the items which should be falsified by experimental measurements. This issue of if a nonsingular beginning as relevant to the formation of initial coherent states, should be vetted experimentally as well as numerically/ analytically, preferably by review of the questions as given by Corda in [36] [37] [38] as far as the formation of gravity from a consistent modeling stand point.
Finally, since we have also brought up look quantum gravity, LQG, it is useful to note, as given by [51] that LQG also has its own quantum bounce, and a nonsingular beginning with subsequent inflation, with especially [30] being critically important as to the idea of a non singular quantum bounce.
Note though, that unlike the work cited in [49] [50] that there is no reference made to additional dimensions in either [30] [51] which means that the nonsingular bounce as given in [30] [51] would have a very different character than what we would look at as to [49] [50] , which is an experimentally important difference we hope to falsify, if we can ever get to the point of eliminating the space-time singularity all together.
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 11375279.