1. Introduction
Yaw rate [1] [2] estimation is critical for Traction Control Systems (TCS) [3] and Electronic Stability Control (ESC) system [4] . Many researchers, such as Carlson and Gerdes [5] , Carlson et al. [6] , Shin et al. [7] , Hac and Simpson [8] , Chee [9] , and Wielitzka et al. [10] have worked on new methodologies for yaw rate estimation. It usually takes many years for these new methodologies to be proven production viable. However, the yaw rate estimation during steady-state cornering is relatively simple. Commercial software for ESC products typically use simple models for yaw rate estimation to determine the activation of the system. The accuracy of the yaw rate estimation is critical since any error in the yaw rate estimation may cause the system either to falsely activate, activate too late, or not activated when needed. Calibration engineers spend much of their time trying to minimize the estimation error. Based on experiences, calibration engineers are well aware of the fact that the estimation should be dependent on the weight condition of the vehicle. However, due to the length of the calibration process and the always tight development deadline, it is not desirable to calibrate the ESC system for multiple weight conditions. In addition, it is not straightforward to estimate the weight condition, therefore, calibrations for specific weights may not be useful. Of the different weight conditions, the two most commonly referred ones are Lightly Loaded Vehicle Weight (LLVW) and Gross Vehicle Weight (GVW). Usually calibration engineers focus their effort in optimizing the vehicle performance for the LLVW condition since most of the customer demonstrations are carried out under this condition. The GVW condition will be tested during the final validation process.
In this paper, the impact of vehicle loading and its distribution on the estimation of yaw rate is analyzed. An improved methodology for yaw rate estimation is proposed without adding much complexity to the calibration process. The steady-state model [11] is introduced in Section 2 to evaluate the impact of vehicle loading on the yaw rate estimation. Sections 3 and 4 contain the simulation based analysis of two loading conditions: constant and different center of gravity positions. A new methodology is proposed in Section 5 to reduce the error in yaw rate estimation. Conclusions and discussion are presented in Section 6.
2. Yaw Rate as a Function of Speed and Steering Angle
To illustrate the idea of the new methodology, we use the bicycle model for the vehicle [11] . In steady-state cornering, the steering angle δ (degree) and the radius of turn R (meter) are related by the following equation
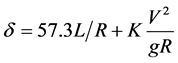 . (1)
. (1)
where L is the wheel base (m), V is the vehicle speed (m/s), K is the understeer gradient, and g is the gravitational acceleration (m/s2). Solving for R, we get
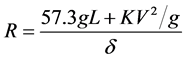 . (2)
. (2)
But the yaw rate is given by
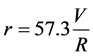 . (3)
. (3)
where r is the yaw rate (deg/s) and 57.3 is the conversion factor from radian to degree [11] . Substituting Equation (2) into Equation (3) to get
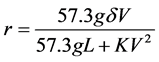 . (4)
. (4)
The understeer gradient is given by
 . (5)
. (5)
where the front and rear corning coefficients 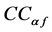 and
and 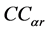 are tire characteristics [5] [11] . A typical cornering coefficient is plotted in Figure 1. Under normal conditions, the percent of rated load will be between 75% and 100%. However, to illustrate the nonlinear characteristic of the cornering coefficient,
are tire characteristics [5] [11] . A typical cornering coefficient is plotted in Figure 1. Under normal conditions, the percent of rated load will be between 75% and 100%. However, to illustrate the nonlinear characteristic of the cornering coefficient,
the range of 25% - 200% of rated load is plotted. Equations (4), (5), and Figure 1 will be used to study the error in the yaw rate model due to the loading condition variation.
In order to study the impact of weight and its distribution on the yaw rate, two vehicle loading conditions are analyzed: 1) The weight is increased from LLVW to GVW while maintaining the same center of gravity (CG) location; 2) GVW with CG at different locations. These two cases are more general than the typical GVW loading condition specified by the vehicle OEM since the CG location can be shifted to various positions.
3. Same CG with Different Weights
If the weight is added at the CG of LLVW, the CG will not change. However, there are two additional constraints: the loads to the front and real axels must be within the corresponding axel loading ratings. As a result, the extra weight added to the vehicle may be less than the difference between GVW and LLVW. The exact maximum weight that can be added at the CG location for LLVW can be easily calculated.
The following set of vehicle parameters are used to calculate the yaw rate estimation:
§ L = 9.4 ft;
§ GVW = 5700 lb;
§ LLVW = 4600 lb;
§ LLVW distribution: front 55%, rear 45%;
§ Rated load for tires = 2050 lb;
§ Front axle rating = 3000 lb;
§ Rear axle rating = 3200 lb;
§ Steering ratio = 17 degree;
§ Cornering coefficient: Figure 1.
For simplicity, the steering wheel angle is assumed to be 20 degrees. The impact of steering angle will be discussed later. Using the formulas given in section 2 one can calculate the yaw rate for any given vehicle speed. The resulting yaw rate of the following two extreme cases can be plotted as a function of the vehicle speed: one is the LLVW, which is close to the calibration condition for the controller; the other is with the heaviest loading without violating the GVW and axle rating limitation (Labeled as GVW in Figure 2). A MATLAB mfile was created to search for such heaviest load.
Intuitively, all other weights should have the yaw rate between the two extreme cases. This was verified with MATLAB simulation. Note that the difference between LLVW and GVW in Figure 2 is small. In other words, if the CG remains the same then the vehicle loading condition has a negligible impact on yaw rate during steady state corning. A contributing fact for this phenomenon is that the extra weight can be added is less than the difference between GVW and LLVW. In other words, the axel rating may be violated before the weight reaches GVW. In addition, the difference in yaw rates for LLVW and GVW increases as the vehicle speed increases. This phenomenon can be understood by observing that in Equation (4), the difference in the yaw rates for GVW and LLVW is caused by the concerning coefficient K. The term KV2 in the denominator increases as the vehicle speed increases.
4. GVW with Different CGs
In general, when the load is added to the vehicle, the CG location can shift. To analyze this condition, the weight of the vehicle is assumed to be GVW. The position of the CG for GVW is varied such that the axel load ratings are not exceeded. A one dimensional search in MATLAB showed that there were two extreme positions to adding weights to the GVW condition without violating the
![]()
Figure 2. Yaw rates for LLVW and maximum loading without changing CG.
axle rating, one is close to the front axle and the other is close to the rear axle. Weight can be added up to the GVW condition to any points between these two extreme positions without violating the axle rating.
The two extreme cases are plotted in comparison to the LLVW condition in Figure 3, where GVW_front is the loading condition when the weigh is added to as close to the front axle as possible and GVW_rear is the loading condition when the weigh is added to as close to the rear axle as possible.
Comparing to Figure 2, one can see that when the CG location is different from that of LLVW, the impact on the yaw rate is significant at high speed. Since the yaw rate estimation model is calibrated under LLVW condition, this means the worst case error can as much as 8 degree/s at a speed of 60 miles per hour (mph). This error can cause the ESC system to be sluggish in response under GVW conditions when ESC activation is needed. This is typically handled by the calibration engineers by reducing the ESC activation threshold. However, reducing the activation threshold may cause false activation under LLVW condition.
5. Yaw Rate Estimation Compensation
Based on the analysis in Sections 3 and 4, it is easy to see that one should not use the yaw rate estimation model calibrated at the LLVW condition, since the LLVW condition is very close to one of the extreme cases. If the vehicle loading condition can be estimated using the data from brake control action such ABS, traction control, or ESC, then a simple interpolation of the LLVW and GVW curve would provide an improved yaw rate estimation. Of course, the estimation error will depend on how good the loading condition estimation is. The loading condition can be estimated based on front and rear wheel slips, vehicle longitudinal/lateral accelerations, and other information that is available to the ESC system.
![]()
Figure 3. Yawrates at LLVW/ GVW with different CGs.
If the loading condition cannot be estimated, one can take the average of the two extreme cases, i.e., the GVW_rear curve in Figure 3 and the GVW curve in Figure 2, as the yaw rate estimation. An optimal loading position is first searched in MATLAB such that by adding the weight at this position would cause the yaw rate curve to be in the middle of the two extreme curves.
Assuming that the ESC system is calibrated under the LLVW loading condition, one can simply add a yaw rate compensation that is equal to the difference between the optimal loading curve and the LLVW loading curve in Figure 4. The result will have the yaw rate estimation error reduced by 50%.
Recall that a simplifying assumption was made in order to plot the curves in Figures 2-4, that is the steering wheel angle is constant. In order to come up with the actual compensation amount, the results plotted in Figures 2-4 are repeated for different values of steering wheel angle. The yaw rate estimation correction amount is plotted in Figure 5 for various values of the steering angel. Note that the yaw rate compensation amount increases as the steering angle increases. This is because the steering angel appears in the numerator in Equation (4). Larger steering angel implies larger yaw rate and the error in yaw rate estimation. Based on the value of the steer wheel angle, one selects the corresponding curve in Figure 5 as the yaw rate compensation as a function of vehicle speed.
Next, the robustness of this new methodology will be analyzed. The cornering coefficient curve will have a tolerance. It is desirable to understand what impact any change in the cornering coefficient would have on the overall result.
In Figure 6 and Figure 7, the curves in Figure 4 are replotted with the cornering coefficient value increase by 0.05 and decreased by 0.025, respectively. It can be seen that the yaw rate estimation error increases when the cornering coefficient is decreased and the yaw rate estimation error decreases when the
![]()
Figure 4. Optimal loading condition for yaw rate estimation model calibration.
![]()
Figure 5. Yaw rates compensation based on speed and steering wheel angle.
![]()
Figure 6. Yaw rates compensation based on speed and steering wheel angle.
cornering coefficient is increased.
6. Conclusions and Discussion
The impact of the weight and its distribution on the yaw rate estimation during steady-state corning is illustrated using a simple bicycle model. Through simulation in MATLAB, the loading condition is identified as an important source of yaw rate estimation error. With the proposed simple change to the calibration process, the yaw rate estimation error can be greatly reduced. One can apply this methodology using more complicated vehicle models, such as a Carsim model. By plotting the yaw rate vs speed function with different steering wheel angles and different loading conditions, one can identify the two extreme loading
![]()
Figure 7. Yaw rates compensation based on speed and steering wheel angle.
conditions. The average of the yaw rate for the two extreme cases can be used to find the optimal load position. The compensation amount for yaw rate estimation can be calculated. All these steps can be carried out in a simulation environment. The result can be easily implemented in the existing ESC software. The estimation error is reduced as a result, without any loading information or need for recalibration.
The preliminary result in this paper can be further improved by adding a load condition estimation algorithm, which is still under investigation. The idea is to first estimate the loading condition (how much weight and the CG location) before ESC activation using the longitudinal/lateral acceleration signals and wheel speed signals; for a given loading condition, the yaw rate compensation amount can be calculated off line and store in the software. This would further reduce the impact of loading condition on the yaw rate estimation. Even if complete loading condition cannot be identified, partial information such as the total weight can allow one to further reduce the yaw rate estimation error.