Some Methods of Solution of Problems of Sound Diffraction on Bodies of Non-Analytical Form ()
1. Introduction
There are a large number of numerical methods of a sound scattering studies on ideal and elastic bodies of a non-analytical form. The article presents a theory and a nu- merical experiment of seven such methods. These results were obtained as authors of a review and other researchers.
2. Method of Integral Equations
We discern the ideal non-analytical scatterer in the form of the terminal cylinder with the semi-sphres on its ends (see Figure 1).
The pressure 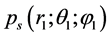 in the scattered wave in the point observation
in the scattered wave in the point observation  is equally [1] [2] [3] [4] [5] :
is equally [1] [2] [3] [4] [5] :
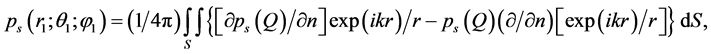 (1)
(1)
where Q―the point of the surface of the scatterer.
Then (1) for the Dirichlet condition at the surface is accepting the appearance:
![]()
Figure 1. The non-analytical smooth scatterer in the form of the cylinder with the semispheres.
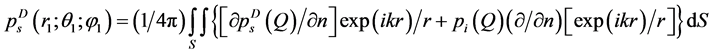 (2)
(2)
For the Neimann’s condition:
 (3)
(3)
The function  we are find from the solution of the non-homogeneous Fredholm equation of the second kind [1] [2] [3] [4] [5] :
we are find from the solution of the non-homogeneous Fredholm equation of the second kind [1] [2] [3] [4] [5] :
 (4)
(4)
The integral to the left of (4) must understand in the sense of the main meaning.
With the help Ψ we are find and the scattered pressure  in the any point of the medium
in the any point of the medium :
:
 (5)
(5)
For the Neimann’s condition, we are bring the function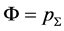 ―the solution of the Fredholm equation of the second kind [1] [2] [3] [4] [5] :
―the solution of the Fredholm equation of the second kind [1] [2] [3] [4] [5] :
 (6)
(6)
The scattered pressure in the point 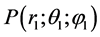 we are express through the function Ф:
we are express through the function Ф:
 (7)
(7)
The scattered pressure  can find either with the help of the integral (2), (3) (for the Fredholm equation of the first kind), or with the help of the Equation (5), (6) (for the Fredholm equation of the second kind).
can find either with the help of the integral (2), (3) (for the Fredholm equation of the first kind), or with the help of the Equation (5), (6) (for the Fredholm equation of the second kind).
The surface S consists of S2 and the surfaces S1 и S3 (see Figure 1).
For the calculation of the integrals (2), (3) and (5), (6) on surface 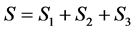 we are choose the grid of the nodal points [2] [3] [4] [5] (Figure 2, Figure 3).
we are choose the grid of the nodal points [2] [3] [4] [5] (Figure 2, Figure 3).
At Figure 4 is present 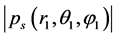 for the chosen parameters by
for the chosen parameters by ![]() (the curve 1 corresponds to method of the T―matrixes, but the curve 2―to the method of the integral equations).
(the curve 1 corresponds to method of the T―matrixes, but the curve 2―to the method of the integral equations).
We are going to spread the method of the integral equations, used in [2] [3] [4] [5] for the ideal non-analytical scatterers, on the elastic shell of the non-analytical form.
In the quality of such scatterer, we are going to consider the terminal isotropic elastic cylindrical shell with the semi-spheres on its ends (see Figure 5). The density of the material of the shell is ρ1, the Lame’s coefficients―λ and μ. The shell was filled in the internal liquid medium with the density ρ2 and the sound velocity C3 and it was placed in the external liquid medium with the density ρ0 and the sound velocity C0.
![]()
Figure 2. The coordinate system, connected with cylinder.
![]()
Figure 3. The coordinate system, connected with hemispheres.
![]()
Figure 4. The modulus of the angular distribution of the scattered pressure.
![]()
Figure 5. The elastic shell in the form of the terminal cylinder with the semi-spheres.
At the shell falls the plane harmonic wave with pressure pi under the angle Θ0 and with the wave vector![]() .
.
As was shown in [2] - [8] , the initial equation is integral equation, having the sense of the generalized Huygen’s principle, for the displacement vector ![]() of the elastic shell:
of the elastic shell:
![]() (8)
(8)
where ![]() is the stress vector;
is the stress vector; ![]() is the single vector of the external along the relation to S normal;
is the single vector of the external along the relation to S normal; ![]() is the stress tensor of the isotropic material;
is the stress tensor of the isotropic material; ![]() is the displacement Green’s tensor;
is the displacement Green’s tensor; ![]() is the stress Green’s tensor; if
is the stress Green’s tensor; if ![]() concerns to the point of the surface S, in the left part of the Equation (8) will stand
concerns to the point of the surface S, in the left part of the Equation (8) will stand![]() .
.
The second integral equation presents the Kirchhoff integral for the diffracted pressure ![]() in the external medium [2] [9] :
in the external medium [2] [9] :
![]() (9)
(9)
where![]() ;
; ![]() is the scattered pressure in the point P1; C(P1) is the numerical coefficient, equal 2π, if
is the scattered pressure in the point P1; C(P1) is the numerical coefficient, equal 2π, if ![]() and 4π, if P1 out Sa; Sa is the external surface of the shell; Q is the point of the external surface of the shell.
and 4π, if P1 out Sa; Sa is the external surface of the shell; Q is the point of the external surface of the shell.
For the pressure ![]() in the internal liquid medium in the point M1 is got the third integral equation:
in the internal liquid medium in the point M1 is got the third integral equation:
![]() (10)
(10)
where ![]() is the point of the internal surface of the shell;
is the point of the internal surface of the shell;
![]()
Sb is the internal surface of the shell.
To the integral Equations (8), (9) and (10) are added the boundary conditions on the external (Sa) and internal (Sb) surfaces of the shell [2] [3] [4] [5] [6] .
For choosing boundary conditions we will have the integrals of the two types: the integrals with the isolated special point and the integrals which are considered of the sense of the principal meaning. The method of the calculation of the second types was described in [2] .
Applying the normal modes and image sources methods for a harmonic signal in the planar waveguide is equivalent [10] . Harmonic signal in the plane waveguide was studied previously enough at the great length [2] [11] [12] . At the basis of the imaginary sources and imaginary scatterers method the problem of scattering of the pulse signals on elastic spheroidal bodies is solved, accommodated in the plane waveguide with the ideal boundary conditions. The impulse signals put the energy, therefore they are propagated with the group velocity, which lies in the principles of the imaginary sources and imaginary scatterers method (method of normal waves of the waveguide is not applicable in this case). Temporal and spectral characteristics of the pulse signals reflected and diffracted from the spheroidal shape elastic bodies are obtained for the first time in this paper.
The spectrum ![]() of the sound pulse of the source with the harmonic filling has the following appearance [13] :
of the sound pulse of the source with the harmonic filling has the following appearance [13] :
![]() (11)
(11)
where:![]() ―the frequency of the filling of the impulse; n―the number of the oscillation periods of the harmonic signal in the pulse;
―the frequency of the filling of the impulse; n―the number of the oscillation periods of the harmonic signal in the pulse;![]() ―the circular frequency.
―the circular frequency.
The spectrum ![]() is connected with
is connected with ![]() of the source by the return Fourier transform:
of the source by the return Fourier transform:
![]() (12)
(12)
The spectrum of the scattered (reflected or transmitted) signal ![]() is by the product of the spectrum
is by the product of the spectrum ![]() at the corresponding meanings of the angular characteristic of the scattering of the spheroidal shell
at the corresponding meanings of the angular characteristic of the scattering of the spheroidal shell ![]() (
(![]() and
and![]() ―the angular coordinates of the point of the observation). The spectrum diffracted signal
―the angular coordinates of the point of the observation). The spectrum diffracted signal ![]() depends on
depends on ![]() and
and![]() .
.
Similarly to (23) with the use of ![]() and
and ![]() images of
images of ![]() and
and![]() ―scattered and diffracted pulses respectively [2]
―scattered and diffracted pulses respectively [2]
![]() (13)
(13)
![]() (14)
(14)
Considering the elastic shell into the liquid layer with the thickness H and the constant sound velocity the boundary conditions will be at follows: at the upper boundary of the waveguide Dirichlet condition is fulfilled, at the lower boundary―Neumann condition [2] [3] (Figure 6).
The scatterer centre is fixed at the distance of ![]() from the bottom and at the horizontal distance R; the point-source Q of the impulse sound signal is placed the depth
from the bottom and at the horizontal distance R; the point-source Q of the impulse sound signal is placed the depth ![]() from the centre (Figure 6).
from the centre (Figure 6).
The scattered field for the non-analytical form elastic shell has been determined either with the help of the method of the integral equations [2] [3] [14] . As such a scatterer here the terminal isotropic elastic cylindrical shell with the semi-spheres on its ends (see Figure 5) is going to be considered.
3. Method of Green’S Functions for Ideal Scatterer
We consider non-analytical body, the surface of which does not apply to coordinate symones with divided variables in the scalar Helmholtz equation. We examine this non-analytical scatterer in the form of a finite circular cylinder bounded on the sides of the hemispheres (Figure 1).
Sound pressure, scattered by this body, can be found one of the numerical methods for the solution of diffraction problems [2] [3] [6] [7] [15] - [22] . The method of Green’s f functions [21] [22] , based on the use of mathematical formulation of the principle of Helmholtz-Huygens (Kirchhoff integral), one of the most convenient methods. The algorithm of calculation requires knowledge of the amplitude-phase distribution of the sound pressure and the normal component of oscillatory velocity on some closed surface integration of S, that includes the lateral surface of the cylinder S2 and the surface of hemispheres S1 and S3 (Figure 1).
![]()
Figure 6. The mutual disposition of the impulse point-sources and scatterers in the plane waweg.
![]() (15)
(15)
where ps(P)―the sound pressure scattered by the body, P―the point of observation, which has a spherical coordinates:![]() ; Q―the point of the surface S; ps(Q)―the sound pressure in the point Q; G(P, Q)―Green’s function of the free space, satisfying the inhomogeneous Helmholtz equation.
; Q―the point of the surface S; ps(Q)―the sound pressure in the point Q; G(P, Q)―Green’s function of the free space, satisfying the inhomogeneous Helmholtz equation.
In the (15) Green’s function is selected as a potential point source:
![]() (16)
(16)
where![]() ―the wave number,
―the wave number,![]() ―the length of a sound wave in the liquid environment, R―the distance between the points P and Q.
―the length of a sound wave in the liquid environment, R―the distance between the points P and Q.
Using relative arbitrariness of the choice of Green’s function, you can get the Kirchhoff formula options, consisting of a single member:
![]() (17)
(17)
![]() (18)
(18)
By using formulas (17), (18) is considerably simplified computational procedure: you want to define only one of the parameters (ps(Q) or dps(Q)/dn) on the surface S. However, in this case, the match of the surface S with a coordinate the surface one of coordinate systems in which it is possible separation of variables is necessary. Thus, application of Green’s functions for analytical surfaces (infinite cylinder and sphere) faces of these surfaces, interconnected is the main feature of this method.
The possibility of such a method and test calculations of the scattered field were considered in [23] [24] . For example, an experiment at the decision of a test problem [23] for the calculation of the far field of a point source (group of point sources) directly and through (17), (18) has shown that in the considered range of wave sizes of the results obtained by these two methods, good enough coincide. When solving the problem of diffraction to determine the values of ps (Q) and dps(Q)/dn on the surface S you can use the following expression:
1) For the homogeneous Dirichlet conditions (ideally soft body), pressure scattered waves on the surface S have the form:
![]() (19)
(19)
2) For the homogeneous Neumann conditions (ideally rigid body):
![]() (20)
(20)
where p, (Q)―the sound pressure of the incident wave in point Q. When determining the values pt(Q) you can use the expression for the scalar potential of the plane monochromatic wave single amplitude of the incident on the body from a source located at infinity.
This potential for a perfectly reflective sphere is natural functions in solving the Helmholtz equation in a spherical coordinate system has the following form [6] :
![]() (21)
(21)
![]()
The expression (21) is simplified when considering the axis-symmetric problem (dependence on the coordinate ![]()
![]() (22)
(22)
For scatterer in the form of a perfectly reflecting cylinder scalar potential incident plane harmonic waves unit amplitude of the wave vector, ![]() , aimed at the angle
, aimed at the angle ![]() to the z axis of the cylinder, folding natural functions solutions to the Helmholtz equation in a circular cylindrical coordinate system:
to the z axis of the cylinder, folding natural functions solutions to the Helmholtz equation in a circular cylindrical coordinate system:
![]() (23)
(23)
In the case of the plane problem of the wave vector к perpendicular to the z axis of the cylinder and expression (23) is simplified [6] :
![]() (24)
(24)
4. Results of Numerical Experiment
For calculation of integral (17) and (18) on the surface S the quadrature formulas is used. A step of integration over the surface S in the axial and circumferential directions ![]() in the system of nodal points must not exceed 0.5l (Figure 2 and Figure 3).
in the system of nodal points must not exceed 0.5l (Figure 2 and Figure 3).
Using the method of Green’s functions were calculated the equivalent radius ![]() of the ideal non-analytical body for several values of wave size ka (where a is the radius of cylinder and hemispheres of the non-analytical scatterer) and different angles of irradiation (Figures 7-9).
of the ideal non-analytical body for several values of wave size ka (where a is the radius of cylinder and hemispheres of the non-analytical scatterer) and different angles of irradiation (Figures 7-9).
![]()
Figure 7. Angular diagrams ![]() at the angle of the incident
at the angle of the incident![]() .
.
![]()
Figure 8. Angular diagrams ![]() at the angle of the incident
at the angle of the incident![]() .
.
![]()
Figure 9. Angular diagrams ![]() at the angle of the incident
at the angle of the incident![]() .
.
The analysis of equivalent radiuses ![]() presented on these pictures, permit to make the following conclusions:
presented on these pictures, permit to make the following conclusions:
1) The angular position of reflecting and diffraction lobes totally correspond to the physical representations;
2) The angular characteristics ![]() of submarine non-analytical object are rather similar to the angular diagrams of spheroid bodies [2] [25] .
of submarine non-analytical object are rather similar to the angular diagrams of spheroid bodies [2] [25] .
At all figures clearly observed diffraction (shadow) petal, and it grows and shrinks with increasing frequency. On Figures 7-9, the mirror petal is shows, which is similar to the shadow petal with increasing frequency, but in contrast, limited asymptotically. You may notice that the angular diagrams of the non-analytical scatterer are very similar to the angular characteristics of the scattering elongated spheroids (ideal and elastic) with the ratio of the semi-axes 1:10 [2] [17] [25] [26] . In contrast to works [18] , which used a method of integral equations and were calculated for non-analytical body with short cylindrical insert, in this study cylindrical insert was much longer. Values equivalent radius at other angles of incidence is given in works [27] [28] .
5. Green’s Functions Method for Elastic Scatterers
The solution of the problem of the sound scattering by an elastic shell of the non- analytical form is based an article [29] . The Green’s functions method is approximate because it does not take account the interaction between individual elements forming a compound body of non-analytical form. The interaction between scatterers shaped as spheroids and elliptic cylinders in [2] and this interaction was negligibly small. In addition, the sound scattering characteristics calculated for bodies with mixed boundary conditions by the Green’s function method namely the Sommerfeld method (the method of un-determined coefficients [2] [25] ), and the agreement between the results was fairly good.
As non-analytical bodies considered two structures:
1) A finite-length circular cylindrical elastic shell limited an the ends by the two halves of a prolate spheroidal shell (Figure 10);
2) The same end cylindrical shell bounded the ends by the two halves of a spherical shell (Figure 5).
![]()
Figure 10. The cylindrical shell with the semi-spheroidal shells.
In article, [29] gave a decision acoustic scattering problems to the constituent parts of no analytical bodies. For cylinder and spheroidal shells are used Debye and Debye-type potentials. In [29] the angular scattering characteristics of such com-pound bodies with different wave sizes are calculated.
We consider a compound elastic shell formed by a finite cylindrical shell whose ends are closed by two hemi spherical shells of the same diameter (Figure 5). To apply the Green’s function method, it is necessary to take the solution to the axi-symmetric problem of plane wave diffraction by an elastic spherical shell in terms of dynamic elasticity theory [30] and transform this solution to the three-dimensional version. The resulting solution little differs from that obtained above for the three-dimensional problem of diffraction by a spheroidal elastic shell [2] [25] [26] [31] .
Figure 11 and Figure 12 show the absolute values of the angular characteristics ![]() (in the XOY plane,
(in the XOY plane,![]() ) for non-analytical elastic scatterer in the form of a cylindrical shell connected with to spherical shells (Figure 3) the following parameters: ka = 0.523 (Figure 11) and ka = 0.941 (Figure 12).
) for non-analytical elastic scatterer in the form of a cylindrical shell connected with to spherical shells (Figure 3) the following parameters: ka = 0.523 (Figure 11) and ka = 0.941 (Figure 12).
The method of Green’s functions in combination with analytical methods can be used for the solution of tasks of diffraction of plane sound wave on elastic isotropic scatter of non-analytical form, that consists of circular cylindrical shell of terminated length L and radius r0, bounded at the butts by the halves of elongated spheroidal shell [28] (Figure 10).
The internal surface of the spheroidal shell is given by coordinate ![]() (with the proportion of the axes of the inner spheroid 10:1 and inter-focal distance 2h0) , and external-by coordinate
(with the proportion of the axes of the inner spheroid 10:1 and inter-focal distance 2h0) , and external-by coordinate ![]() .
.
The shell material is isotropic, with the density ![]() , coefficients of Lame
, coefficients of Lame ![]() and
and![]() , module of Jung E, inside is the gas with density
, module of Jung E, inside is the gas with density ![]() , coefficient of volumetric compression
, coefficient of volumetric compression ![]() and sound rate
and sound rate ![]() .
.
The scatterer is placed in ideal compressed liquid with density ![]() and coefficient of volumetric compression
and coefficient of volumetric compression ![]() . The potential of sound wave is submitted to scalar equation of Helmholtz.
. The potential of sound wave is submitted to scalar equation of Helmholtz.
The amplitude-phase distribution of the sound pressure and of normal component of vibrating velocity in the points of this non-analytical surface is found from the strict solution of tridimensional boundary tasks of dynamic theory of elasticity on the endless
![]()
Figure 11. The modulus of an angular characteristic.
![]()
Figure 12. The modulus of an angular characteristic.
elastic cylindrical surface and elastic spheroidal surfaces, respectively.
The schemes of solution of axially symmetric tasks of diffraction on elastic cylinder and spheroid are rather similar: in both cases the vector potential ![]() has the single nonzero component
has the single nonzero component ![]() . The unknown coefficients of potentials’ expansion of falling and dispersed waves, of scalar potential of the surface, of potentials of Debye U and V, as well as of potential of gas, filling the surface, are found from the physical boundary conditions on the external and internal surfaces of the shell [32] .
. The unknown coefficients of potentials’ expansion of falling and dispersed waves, of scalar potential of the surface, of potentials of Debye U and V, as well as of potential of gas, filling the surface, are found from the physical boundary conditions on the external and internal surfaces of the shell [32] .
Although on the spheroid these coefficients are found not in the enclosed form, but using the method of truncation from the infinite system of equations.
What is more, while finding the solution of tridimensional task of diffraction on elastic speroidal scatterer the vector potential ![]() is presented by the potential of Debye U and V [2] [19] [32] :
is presented by the potential of Debye U and V [2] [19] [32] :
![]() (25)
(25)
where ![]() ―is the radius-vector of the view point of,
―is the radius-vector of the view point of, ![]() ―is the wave number of transverse wave in the material of the shell.
―is the wave number of transverse wave in the material of the shell.
The sound pressure in the far-field can be found by one of the numerical methods, among those is the comfortable method based on the usage of mathematical formula of Helmholtz-Huygens ‘Principle (integral of Kirchhoff) [25] :
![]() (26)
(26)
where r―is the distance between the point Q on the surface of the shell and the point P with coordinates r1, θ1, φ1 in the far-field.
The Green’s functions in (26) are taken in the form of potential of the point-source. The quadrature formulas are used for finding of this integral, and here the integration step (sampling) of the surface of the scatterer should not exceed 0.5l0, where l0―is the length of the plane monochromatic wave, falling from the liquid onto the surface of the scatterer.
The Green’s functions in (26) are taken in the form of potential of the point-source. The quadrature formulas are used for finding of this integral, and here the integration step (sampling) of the surface of the scatterer should not exceed 0.5l0, where l0―is the length of the plane monochromatic wave, falling from the liquid onto the surface of the scatterer.
6. Methods of Kupradze, T-Matrix and Geometrical Theorie of Diffraction
The other way of solving the task of sound diffraction on elastic isotropic body with non-analytical surface is based on the method of Kupradze [16] . According to this method the scattered pressure ![]() and the vector of displacement of elastic body
and the vector of displacement of elastic body ![]() can be presented in the form of potentials, focused on the surface of the elastic body S:
can be presented in the form of potentials, focused on the surface of the elastic body S:
![]() (27)
(27)
![]() (28)
(28)
where![]() ―is the radius-vector of the surface point S;
―is the radius-vector of the surface point S; ![]() and
and![]() ―are the unknown scalar and vector densities, the function
―are the unknown scalar and vector densities, the function ![]() and matrix
and matrix ![]() differ from the Grin function of Helmholtz’ operator and from the tensor of displacements of Grin by the constant multipliers:
differ from the Grin function of Helmholtz’ operator and from the tensor of displacements of Grin by the constant multipliers:
![]() (29)
(29)
From the common characteristics of wave and elastic potentials we find that ![]() and
and ![]() satisfy the system of the four integral equations on the surface S:
satisfy the system of the four integral equations on the surface S:
![]() (30)
(30)
where![]() ―are the tangents to S stress;
―are the tangents to S stress;![]() ―is the single vector of the normal to S, the dash means that the so-called direct values of these parameters. The numerical solution of the system (16) on computers for elongated elastic bodies is marked by considerable processing difficulties. The asymptotic methods, permitting to get the approximate solutions of the system (14) are used in (16); these methods are based on asymptotic formulas for integrals, received in [17] .
―is the single vector of the normal to S, the dash means that the so-called direct values of these parameters. The numerical solution of the system (16) on computers for elongated elastic bodies is marked by considerable processing difficulties. The asymptotic methods, permitting to get the approximate solutions of the system (14) are used in (16); these methods are based on asymptotic formulas for integrals, received in [17] .
The usage of method of T-matrix in the task of sound diffraction on elastic bodies of non-analytical form is examined in [11] . The source system of integral solutions for the displacement vector ![]() of elastic finite cylinder with spherical shell plates (Figure 1) is got with the help of [19] , and the integral equation for
of elastic finite cylinder with spherical shell plates (Figure 1) is got with the help of [19] , and the integral equation for ![]() substitutes the integral of Kirchhoff:
substitutes the integral of Kirchhoff:
![]() (31)
(31)
The equation for ![]() is received from (1) with addition of vector of displacement
is received from (1) with addition of vector of displacement ![]() in the falling wave, and with conversion of module of displacement in the expressions for tensor of stress of Cauchy
in the falling wave, and with conversion of module of displacement in the expressions for tensor of stress of Cauchy ![]() and tensor of stress of Grin
and tensor of stress of Grin ![]() in nil. As the result, the second integral equation gets the form of [17] :
in nil. As the result, the second integral equation gets the form of [17] :
![]() (32)
(32)
where the vector ![]() refers to the point of fluid medium, outside the surface S.
refers to the point of fluid medium, outside the surface S.
The solution of the received system of the two integral equations is found by the method of T-matrix with the use of boundary conditions.
The particular place in the tasks of diffraction on the bodies with non-analytical surface in the sphere of high frequencies is occupied by the geometrical theory of diffraction (GTD), based on the asymptotic methods [2] [33] .
In comparison to ray acoustics (RA), the GTD regards the process of formation of diffraction rays along with reflection and refraction. When the wave falls onto the body or its edge, the boundary shade-light appears for geometrical rays, i.e. the geometro- acoustic solution faces the break that states the formation of additional diffraction fields, compensation this break.
The four main additional laws are considered in GTD, in comparison to RA: two of them determine the direction of diffraction rays, two others―their amplitudes:
1) The range of diffraction rays is produced not by all of the falling rays, but:
а) by the rays falling onto the non-homogeneous parts of the body S―edges, ridges, lines of discontinuity in the curvature (Figure 13(a) and Figure 13(b)); b) by the rays contacting the body (Figure 13(c)).
2) When the ray of the primary field falls onto the edge of the body (Figure 13(a)), the diffraction rays radiate from it in all the directions, forming the spherical wave. If the ray contacts the ridge (Figure 13(b)), the diffraction rays form the cone in its each point. The angle ![]() of cone opening is equal to the angle
of cone opening is equal to the angle ![]() between the tangent to the ridge and the falling ray, what means,
between the tangent to the ridge and the falling ray, what means,
![]() . (33)
. (33)
![]()
Figure 13. The varieties of diffraction fields in the terms of geometrical theory of diffraction.
The law of formation of diffraction rays in the sphere of shade of plain convex body differs from the law of rays’ formation at edges and ribs. In this case, the diffraction rays get away from the surface of the shade part of the body and form the slippage waves.
Each ray of the falling wave which contacts the body, from the “surface ray” ![]() (Figure 13(c)) on the surface of the body, that is the geodesic (shortest) line on the surface of the body. The direction of the ray in point T of the horizon
(Figure 13(c)) on the surface of the body, that is the geodesic (shortest) line on the surface of the body. The direction of the ray in point T of the horizon![]() , i.e. at the point of formation, coincides with the direction of the falling ray. The number of the rays of slippage wave gets tangentially off the range of surface rays.
, i.e. at the point of formation, coincides with the direction of the falling ray. The number of the rays of slippage wave gets tangentially off the range of surface rays.
3) The amplitude of diffraction ray is proportionate to the amplitude of the formatting primary ray in the impact point. The diffraction fields can be presented in the formula:
![]() (34)
(34)
where S―is the eikonal (function, determing the phase structure of the field―the system of the wave front); J―is the Jacobian of transition to the ray coordinates―the parameter, proportionate to the area of cross-section of rays of the tube;![]() ―the gradients of the falling and diffraction rays;
―the gradients of the falling and diffraction rays;![]() ―the amplitude of the falling wave: in the point of the edge or the rib, where the concerned ray originates, or on the point of the horizon, where the surface ray producing the concerned diffraction ray, appears.
―the amplitude of the falling wave: in the point of the edge or the rib, where the concerned ray originates, or on the point of the horizon, where the surface ray producing the concerned diffraction ray, appears.
The parameter ![]() is named the coefficient of diffraction. It is received regarding the fourth law of GTD.
is named the coefficient of diffraction. It is received regarding the fourth law of GTD.
4) The coefficient (matrix) of diffraction D is determined by local features of body’s geometry in the area of the falling ray (in the case of edges and ribs) or in the area of the surface ray between the falling point and take-off point of diffraction ray (in the plain body).
In terms of physics![]() ―is the amplitude of the source, corresponding to the ray that gets off on the direction
―is the amplitude of the source, corresponding to the ray that gets off on the direction ![]() in the case of the falling of the plain wave with singular amplitude in the direction
in the case of the falling of the plain wave with singular amplitude in the direction![]() .
.
The notion of diffraction coefficient in the general case can be defined more precisely. Thus, if the amplitude of the primary field converts into zero in the ray that produces diffraction rays, then the amplitude of diffraction field will not be equal to zero, i.e. the formula (18) cannot be used. In this case the diffraction field will be proportionate to the value of the first derivative of the amplitude of the primary field along the front.
The algorithm of solution of the task of diffraction consisting of 3 rules is based on the laws of GTD:
1) The solution is found as the result of number of the fields of ray type:
![]() (35)
(35)
One of the components is the primary field. Each of the fields differs from zero in the area with the boundary of the body surface and the shade-light boundary of the field.
2) All the sum (33) components, except the primary field (it is considered to be defined) are determined from the primary field according to the laws of RA and of GTD.
It should be kept in mind that the reflected, refracted and diffraction fields can be formed from the primary field not only directly but also as the result of the complex sequence of reflections, refractions and diffractions.
1) The question of the choice of the coefficients of diffraction is important in the process of calculations of diffraction fields. According to the fourth law of GTD, the coefficients of diffraction are equal to all bodies that possess equal local geometrical features and the features of geometry of the falling wave. Here logically appears the third rule of algorithm of diffraction task.
2) The coefficient of diffraction in the present task is found from the analysis of the precise solution of the simple (model) task, close in geometry. For example, in the case of diffraction of the field ![]() on the curved opening in non- plane screen the model task is the task of diffraction of the plane wave on semi- surface, touching the surface of the screen and the edge of the tip in the examined point.
on the curved opening in non- plane screen the model task is the task of diffraction of the plane wave on semi- surface, touching the surface of the screen and the edge of the tip in the examined point.
The usage of GTD is limited in the present number of solutions because the coefficients of diffraction D are determined in the model tasks. In the present the model tasks for numerous two-dimensional cases-fir diffraction on the wedge, plain cylinder, etc.― are solved. In the model three-dimensional tasks, we frequently have to use the approximate results.
7. Method of Finite Elements
The method of the finite elements (MFE) and its variations allow getting the solutions of tasks of sound radiation of elastic bodies of nearly all forms. Here we consider, for example, the possibility of common use of MFE with the method of Grin functions for numerical solution of task of the distant field of sound radiation by extended spheroid shell, under the influence of the point sources on its surface (Figure 14):
The choice of this body is caused by the definite solution of the task of sound radiation of spheroid shell under the influence of point sources on its surface that was received using the theorem of reciprocity from the three-dimensional boundary task of
![]()
Figure 14. Extended spheroid shell, under the influence of the point sources on its surface.
diffraction of plane monochromatic wave on this shell; the solution is presented in [18] [34] . This task can be interpreted as the task of sound radiation of elastic body under the influence of turbulent pulsations of liquid flow, and the calculation based on the focused force that is stipulated by this pulsation, presents certain interest. In this case, it is useful to compare the results of the numerical solution with analytical solution results for valuation of its accuracy.
The geometrical and physical parameters of the shell are similar to those presented on Figure 14. The point sources of harmonic signal are situated at the ends of the shell at the points A and B; these sources imitate the turbulent pulsation and produce some amplitude-phase distribution (AFD) of the sound wave potential on the external surface ![]() and in the liquid surrounding the shell.
and in the liquid surrounding the shell.
The numerical solution of the task is made in two stages [18] :
1) The calculation of the values of sound wave potential and its gradient on the closed test area in the nearest field (of the Fresnel zone), that are created by the point sources;
2) Re-calculation of received results in the distant field (in the Frauenhofer zone).
On the first stage it is necessary to conjugate the solutions of FEM on the surface of area S in the sphere V1, adjoining the shell, with the point analytical solution of equation of Helmholtz in the external endless sphere V2 (Figure 15).
The functional of the full energy if the system “shell-fluid” will have the form:
![]() (36)
(36)
where г д е P and T―are potential and kinetic energies of the shell; w―normal displacement of the shell to the surface ![]() ;
; ![]() и
и ![]() ―potentials of speed of liquid correspondently in volumes V1 and V2 correspondently, that meet the equation of Helmholtz and the condition of radiation on infinity in the volume V2.
―potentials of speed of liquid correspondently in volumes V1 and V2 correspondently, that meet the equation of Helmholtz and the condition of radiation on infinity in the volume V2.
![]()
Figure 15. The conjugation of FEM with the point analytical solution.
The condition of stationary state of E functional leads to fulfillment of equation of the shell movement and of equation of Helmholtz in the sphere V1, as well to equality
of the normal speeds ![]() and
and ![]() and potentials
and potentials ![]() and
and ![]() on the surface S.
on the surface S.
The axial symmetry of the shell and sources of radiation leads to the fact that the displacements of the shell and potentials of liquid speed will not be subject to the surrounding coordinate φ.
The substitution of the forms that approximate the shell displacements and potentials Φ1 and Φ2 in conditions of stationary state of E functional leads to the lineal algebraic system of the solving equations.
For the solving of this task is necessary to use the circular finite elements for: the shell, liquid and filling gas, for conjugation of these elements between one another, as well as the finite elements for modeling of the sphere V2. Using these elements is possible to calculate the nearest field for the arbitrary sources in the form of the shells if spinning. In this case, the numerical calculations are made for the finite-elementary net that consists of 131 elements and 410 focal points (Figure 16).
The AFD of the sound pressure and normal component of vibration speed in the focal points of control surface in the nearest field is initial for the second stage of the task solution.
The sound pressure in the distant field is found with Kirchhoff’s integral, as well as in (26).
The two variants of the forms of control surface were used in the calculations:
Non-analytical in the form of cylinder with hemispheres on the edges (as the most useful from the measuring process organization point of view, Figure 17(a)) and analytical (sphere) (Figure 17(b)).
On the basis of the proposed algorithms in [18] the calculations of angel distribution of sound pressure levels, radiated by elastic spheroid shell, we made; these calculations demonstrated rather satisfactory correspondence of results of analytical and numerical methods.
![]()
Figure 16. The finite-elementary net in the nearest field of the shell.
![]() (a) (b)
(a) (b)
Figure 17. The control surface in the form of: cylinder with hemispheres at the edges (a) and sphere (b).
8. Boundary Elements Method
For the solving of tasks of radiation and diffraction for the bodies of non-analytical surface the boundary element method (BEM) is successfully used during the last years; the numerous scientific works are published on this research area, where the theoretical basis of the method as well as the different aspects of the application are stated [7] [15] [34] .
The bibliography analysis shows that BEM is one of the most relevant and widely used among the other numerical methods of solving the boundary tasks.
The following advantages of BEM (in comparison with FEM, for instance) can be considered when solving the tasks:
1) The sampling of the boundary of the sphere with scatterer, not of the whole sphere, when as the result the additional measures for realization of condition of radiation at infinity are not demanded;
2) The reduction of initial differential equation to the boundary integral equation that presents the exact formulation of the stated task. Here the accumulation of error comes in the process of numerical solution of integral equations in the result of sampling, approximation and calculation;
3) The use of analytical method, true for the whole sphere, provides the potentially higher accuracy than FEM does, where the approximation is committed in every area. In the common case for scatterers of general geometric form the boundary surface is presented in the form of collection of elementary areas [2] [18] [34] .
The conception of formation of isoparameter elements allows converting the key coordinates of every point of initial elements ![]() to the corresponding curvilinear coordinates
to the corresponding curvilinear coordinates ![]() . Here, the element’s geometry (global coordinates) and the main variables (of displacement) are stated using the similar interpolating relations (functions of the form) [18] [34] (Figure 18).
. Here, the element’s geometry (global coordinates) and the main variables (of displacement) are stated using the similar interpolating relations (functions of the form) [18] [34] (Figure 18).
The curvilinear coordinates of every point of the element ![]() will be connected by the key coordinates
will be connected by the key coordinates ![]() in the expressions [2] [18] [34] :
in the expressions [2] [18] [34] :
![]() (37)
(37)
where![]() ―the functions of local coordinates
―the functions of local coordinates![]() ―are described shortly:
―are described shortly:
а) For quadrangular elements:
![]()
![]()
![]()
![]()
b) For triangular elements![]() :
:
![]()
![]()
These correlations present the implicit conversion of surface element to the plane square or the plane equilateral triangle (Figure 18).
The correlations for interpolation of displacements and stress are expressed similarly
![]() (a) (b)
(a) (b)
Figure 18. The initial (a) and the corresponding curvilinear isoparameter (b) boundary elements.
on each element [24] :
![]() (38)
(38)
![]() (39)
(39)
where ![]() and
and![]() ―are the parameters of components of vector of displacement or vector of stress at the nodes.
―are the parameters of components of vector of displacement or vector of stress at the nodes.
While submitting (38), (39) in the equation and using the rule of numerical integration, we get
![]() (40)
(40)
where H and![]() ―are the matrix of coefficients used in the result of numerical integration.
―are the matrix of coefficients used in the result of numerical integration.
Here, we form the integral equation for diffracted pressure basing on (1.15) ![]() at the view point
at the view point ![]() [2] [17] :
[2] [17] :
![]() (41)
(41)
where![]() ―is the numerical coefficient, equal to 2π, if
―is the numerical coefficient, equal to 2π, if![]() , and 4π, if
, and 4π, if![]() . Now we interpolate the components of the vector
. Now we interpolate the components of the vector ![]() on each boundary element in correspondence with (38); the sound pressure on each element is presented, similarly to (38) and (39), in the form of:
on each boundary element in correspondence with (38); the sound pressure on each element is presented, similarly to (38) and (39), in the form of:
![]() (42)
(42)
While submitting (38), (39) and (40) in (41) and completing the numerical integration, we receive
![]() (43)
(43)
where T and D―are matrix of coefficients.
On the next stage we solve the system of Equations (40) and (43) using the boundary conditions.
According to the boundary condition the number of indeterminate stress in Equation (40) can be expressed through pressure:
![]() (44)
(44)
where G and F―are matrix of coefficients, received from matrix ![]() in Equation (40).
in Equation (40).
The distributions ![]() and
and ![]() on the surface S are found from Equations (43) and (44), and then the diffracted sound pressure
on the surface S are found from Equations (43) and (44), and then the diffracted sound pressure ![]() in fluid sphere is calculated using (41).
in fluid sphere is calculated using (41).
In the particular cases, it is possible to use the principle of formation of the net of nodal points for the scatterers possessing the form of axially symmetrical bodies; the principle was used in [27] before. Thus, it is possible to implement the cylinder coordinate system (r, j, z) connected with cylinder, and the spherical coordinate systems (r, θ, j), connected with hemispheres, for the bodies with the surfaces consisting of fragments of cylinders and spheres (hemispheres).
In the process of numerical integration the element of the surface of cylinder with radius ![]() will be equal to
will be equal to ![]() ; for hemisphere the element of the surface in the spherical coordinates is equal to
; for hemisphere the element of the surface in the spherical coordinates is equal to ![]() (Figure 2 and Figure 3).
(Figure 2 and Figure 3).
In the process of formation of the net of boundary elements for this task, the discretization step of the boundary surface in the direction of every coordinate should not also exceed 0.5l0.
According to the theorem of Helmholtz, the displacement vector ![]() can be presented in the form of:
can be presented in the form of:
![]() (45)
(45)
where ![]() ―is the scalar,
―is the scalar,![]() ―is the vector potentials that obey to the scalar and the vector equation of Helmholtz, respectively:
―is the vector potentials that obey to the scalar and the vector equation of Helmholtz, respectively:
![]() (46)
(46)
![]() (47)
(47)
where ![]() ;
;![]() ;
; ![]() and
and ![]() ―are velocities of linear and transverse waves respectively in the material of the scatterer.
―are velocities of linear and transverse waves respectively in the material of the scatterer.
For cylinder surface the vector ![]() is parallel to axis of cylinder, i.e. т.е.
is parallel to axis of cylinder, i.e. т.е. ![]()
Due to the axis symmetry of the task for spherical surfaces the vector potential ![]() will also have the only one component
will also have the only one component ![]() , different from zero:
, different from zero: ![]() , in the spherical coordinate system. Thus, the vector equation of Helmholtz (47) transfers into scalar equation for the only component of vector potential, different from zero:
, in the spherical coordinate system. Thus, the vector equation of Helmholtz (47) transfers into scalar equation for the only component of vector potential, different from zero:
![]() (48)
(48)
The potential of diffused wave, as well as the potentials ![]() и
и ![]() are taken in the forms, corresponding to the plane wave and containing the voluntary constants that are determined from the boundary conditions.
are taken in the forms, corresponding to the plane wave and containing the voluntary constants that are determined from the boundary conditions.
While all the main physical variables are functions of only two coordinates, the displacement vector would also possess two components.
Using the correlations of the generalized law of Hooke for isotropic sphere, not depending of the choice of coordinate systems, it is possible to present the elastic stress on the finite surface through the deformation components, and then through potentials ![]() and
and ![]() [2] [25] :
[2] [25] :
а) For cylindrical surface:
![]() (49)
(49)
![]() (50)
(50)
where![]() ;
;
b) For spherical surface:
![]() (51)
(51)
![]() (52)
(52)
![]() (53)
(53)
where![]() .
.
The following boundary conditions are to be executed at the points of the boundary surface:
a) The normal (radial) component of the displacement vector ![]() is continuous and connected with normal derivate of diffracted pressure
is continuous and connected with normal derivate of diffracted pressure![]() :
:
![]() by
by![]() , (54)
, (54)
where![]() ―are the sound pressures of the falling and dispersed waves respectively; the normal stress
―are the sound pressures of the falling and dispersed waves respectively; the normal stress ![]() is equal to acoustic pressure in liquid:
is equal to acoustic pressure in liquid:
![]() by
by![]() ; (55)
; (55)
b) The pressure tangents are missing:
![]() by
by![]() . (56)
. (56)
While submitting the component of the displacement vector and elastic stress to the boundary conditions (54)-(56) we receive the algebraic systems of equations for every point on the surface for finding out the indeterminate coefficients in equations of potentials ![]() and
and ![]() .
.
The indeterminate coefficients are received using the ratio of determinants by the rule of Cramer, that allows to receive subsequently the distributions ![]() and
and ![]() at the nodes of the boundary elements.
at the nodes of the boundary elements.
The calculation of the diffracted sound pressure ![]() in liquid sphere is processed basing on (26) by numerical integration of quadrature formulas.
in liquid sphere is processed basing on (26) by numerical integration of quadrature formulas.
The task solution of diffraction for the elastic isotropic surface does not differ in principle from the examined solution for constant elastic body: the internal boundary (with filler or vacuum inside the shell) is added, and thus the number of indeterminate coefficients and the number of boundary conditions in (49)-(56) increase.
The additional boundary conditions are formed the following way:
4) The normal stress on internal surface of the shell is either missing (the hollow shell) or is equal to the sound gas pressure (gas filled shell);
5) The absence of the tangent stress on internal surface of the shell.
As the illustration of the testing diffraction task for estimation of accuracy of numerical solution by BEM in [34] the modules of angular characteristics of diffusion of elastic sphere and spheroid were calculated; these modules were compared to the analogical characteristics of the same bodies, received using the analytical solution, and demonstrated rather satisfactory correspondence with the latter (Figure 19 and Figure 20).
![]() (a) (b)
(a) (b)
Figure 19. Modules angular characteristics of spherical scatterers (BEM) when ka = 1, ![]() : (a) solid sphere: 1―tight; 2―steel; 3―aluminum; 4―rubber; (b) spherical shell of thickness h: 1 − kh = 0.01; 2 − kh = 0.03; 3 − kh = 0.05; 4 − kh = 0.1.
: (a) solid sphere: 1―tight; 2―steel; 3―aluminum; 4―rubber; (b) spherical shell of thickness h: 1 − kh = 0.01; 2 − kh = 0.03; 3 − kh = 0.05; 4 − kh = 0.1.
![]() (a) (b) (c)
(a) (b) (c)
Figure 20. Modules angular characteristics of spheroids, ![]() : 1―steel (exact solution); 2―steel (BEM); 3―rubber (BEM); (a) for C = 3; (b) for C = 5; (c) for C = 10; (where
: 1―steel (exact solution); 2―steel (BEM); 3―rubber (BEM); (a) for C = 3; (b) for C = 5; (c) for C = 10; (where ![]() ).
).
Also the results of calculations of scattered characteristics for elastic scatterer with non- analytical surface form (cylinder with hemispheres at the edges), by FEM, are presented there; the results were approximate to the corresponding results of the precise solution for spheroids, received in [2] [25] .
9. Conclusions
The article analyzes seven methods of the solution of the problem of the sound scattering on ideal and elastic bodies of the non-analytical forms: method of integral equations, method of Green’s functions, the method of Kupradze, T-matrix method, the method of the geometrical theory diffraction, the method of finite elements and the boundary elements method. This analysis is supplemented with calculations of characteristics of the sound scattering by ideal and elastic scatterers of non-analytical forms.
The author thanks S. L. Il’menkov for writing sections 7, 8 and A. A. Zubova―for the help with calculations.
Acknowledgements
The work was supported as a part of research under State Contract No. P242 of April 21, 2010, within the Federal Target Program “Scientific and Scientific-Pedagogical Personnel of Innovative Russia for the Years 2009-2013”.