1. Introduction
Due to the high power density and the ill of heat dissipation capability, the operating temperature of three-dimensional integrated circuits (3-D ICs) is higher than that of two-dimensional (2-D) ICs. Recently, to effectively remove the heat in 3-D ICs, the advanced liquid cooling system has been widely discussed [1]. Different from the conventional air cooling system, the liquid cooling system delivers water or refrigerant to microchannels heat sink. The microchannels are etched in the silicon substrate in advance. As pointed out in Ref. [2], the chip, which integrates microchannels, can consume a very high power density (790 W/cm2) without burning down. Reference [3] discretized microchannels into small grids to propose a steady state thermal model for single-phase liquid cooling 3-D ICs. Four extra nodes are added, and a channel merging technique is used to simulate the complicated thermal-wake effect of liquid cooling. In addition, 3D-ICE, a compact transient thermal model was proposed in Ref. [4]. The convection heat transfer that leads to thermal-wake effect is already considered in 3D-ICE, so no extra nodes are required. Based on 3D-ICE, other works use a similar model but develop different system solving methods such as the neural network [5], the operator splitting [6], and the explicit method [7].
Different from the above single-phase liquid cooling systems, the two-phase liquid cooling removes the heat via heat absorption during the evaporation process [8]. After absorbing the heat, the part of refrigerant changes its physical state from liquid to vapor. Therefore, qualifying the fraction of vapor becomes an important issue. Since the heat transfer coefficients (HTCs) at the wall surface between solids and liquids depend on the physical state of refrigerant and the temperature profile of chip, an iterative method, STEAM, was proposed to iteratively solve the steady-state problem [8].
This work provides an accurate temperature profile estimate for the two-phase liquid cooling system of 3-D IC. The inputs are the design structure and material files, and the power distribution in device layers. Different from incorporating the fitting curves for correlating HTCs at the wall surface in STEAM [8], here, we present a multi-linear interpolation method on measurement database of HTCs obtained from [9]. Moreover, the proposed flow considers the change of the thermal conductivities of silicon varying from temperature values since there are appreciable temperature gradients between device layers and microchannel layers. Finally, the output is the temperature profile of design. The main contributions of this work are
By using a local multi-linear interpolation technique with the measurement database to approximate HTCs during the thermal simulation procedure for the two-phase liquid cooling system, the accuracy can be reasonably improved.
Considering the interdependence between the operating temperature and thermal conductivity of silicon does improve the simulation accuracy for two-phase liquid cooling systems.
The remainder of this paper is organized as follows. Section 2 reviews the thermal model for at wophase liquid-cooled 3-D IC. With the thermal model, the proposed thermal simulation algorithm is detailed in Section 3. The experimental results are presented in Section 4, and finally, conclusions are drawn in Section 5.
2. Preliminary
The structure of a liquid-cooled 3-D IC is shown in Figure 1. Interconnect layers contain
![]()
Figure 1. Thermal model of a liquid-cooled 3-D IC with three tiers.
interconnects and dielectric. Each device layer is a thin layer on the top surface of stacked silicon substrate or silicon bulk. Functional blocks of each tier are modeled as power generating sources attached to the thin layer that is close to the top surface of the stacked silicon substrateor the silicon bulk. Microchannels are etched on the silicon substrate as heat sink, and a cover plate layer is placed on the back-side of silicon substrate. The material of cover plate is either Si or Pyrex glass. Through silicon vias are placed in the silicon substrate and cover plate layer. All the boundary surfaces of a 3-D IC are assumed to be adiabatic as boundary conditions.
According to the heat transfer equation, the temperature profile T(r) in solids can be governed by
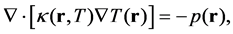 (1)
(1)
and  in fluids (liquid and vapor) can be governed by
in fluids (liquid and vapor) can be governed by
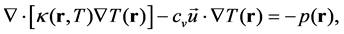 (2)
(2)
Here, 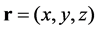 ,
, 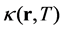 is the thermal conductivity at
is the thermal conductivity at ,
, 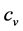 is the volumetric specific heat,
is the volumetric specific heat, 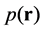 is the power density profile of chip, and
is the power density profile of chip, and 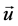 is the velocity of outflow at the surface of the control volume.
is the velocity of outflow at the surface of the control volume.
2.1. Thermal Model of Solid Grids
Using the finite difference method and the duality between thermal and electrical quantities, (1) can be transformed to a SPICE compatible equivalent thermal circuit containing thermal resistances and power sources. For a specific control volume (thermal grid) as shown in Figure 2, each thermal conductance can be calculated as
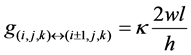 ;
; ;
;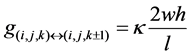 .
.
Here, 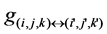 is the thermal conductance between grid
is the thermal conductance between grid  and its neighboring grid
and its neighboring grid .
. ,
,  , and
, and ![]() are the length, width, and height of grid
are the length, width, and height of grid![]() , respectively.
, respectively.
The temperature Ti, j,k at the central node of each solid grid Vi, j,k need to satisfy the following modified nodal analysis (MNA) system.
![]() (3)
(3)
Here, ![]() is an augmented temperature-dependent thermal conductance matrix (contains thermal conductance in solids and HTCs between solids and fluids),
is an augmented temperature-dependent thermal conductance matrix (contains thermal conductance in solids and HTCs between solids and fluids), ![]() is a temperature profile vector of thermal grids, and
is a temperature profile vector of thermal grids, and ![]() is the power profile vector in solids.
is the power profile vector in solids.
2.2. Thermal Model of Two-Phase Grids [8]
Given a thermal grid in liquids as shown in Figure 3, by using the law of energy and mass conservation, the energy balance equation can be written as follows from STEAM [8]
![]()
Figure 2. Equivalent circuit of a solid thermal grid.
![]() (4)
(4)
Here, ![]() is the central temperature at refrigerant thermal grid
is the central temperature at refrigerant thermal grid![]() ,
,![]() is the latent heat of vaporization,
is the latent heat of vaporization, ![]() is the mass flowrate,
is the mass flowrate, ![]() is the temperature on the wall of thermal grid,
is the temperature on the wall of thermal grid, ![]() is refrigerant vapor quality at the interface
is refrigerant vapor quality at the interface![]() , and
, and ![]() is the heat transfer coefficient at the wall surface.
is the heat transfer coefficient at the wall surface.
In (4), the second term on left-hand side represents the heat entering from the microchannel sidewalls into each two-phase thermal grid, and other terms represent heat removal denoted by the latent heat difference of vaporization between the two interfaces ![]() and
and![]() .
. ![]() is correlated with the mass flux
is correlated with the mass flux![]() , vapor quality
, vapor quality![]() , heat flux density
, heat flux density ![]() from solid into two-phase liquid, diameter of microchannels
from solid into two-phase liquid, diameter of microchannels![]() , Prandtl number
, Prandtl number![]() , and the confinement number
, and the confinement number ![]() in different situation. Several nonlinear fitting curves were applied to fit the measurement data for constructing the HTC correlation functions in [9] [10] [11]. Since
in different situation. Several nonlinear fitting curves were applied to fit the measurement data for constructing the HTC correlation functions in [9] [10] [11]. Since ![]() relies on multiple parameters, it is hard to find a suitable fitting form globally, and hence, the existing fitting forms could lead to larger errors in some local regions. Moreover, heat flux
relies on multiple parameters, it is hard to find a suitable fitting form globally, and hence, the existing fitting forms could lead to larger errors in some local regions. Moreover, heat flux ![]() and vapor quality
and vapor quality ![]() are still unknown so as to solving heat transfer equation iteratively. As a result, we propose to use a local multi-linear interpolation technique with the measurement database to approximate
are still unknown so as to solving heat transfer equation iteratively. As a result, we propose to use a local multi-linear interpolation technique with the measurement database to approximate ![]() in each iteration and grids.
in each iteration and grids.
3. Proposed Method
Based on a similar approach as STEAM [8], which the refrigerant temperature values are assumed to be known (they are iteratively calculated during the solving procedure.), (3) and (4) can be combined to build the heat transfer equation for a two-phase liquid- cooled IC as
![]() (5)
(5)
Here, ![]() is a temperature-dependent thermal conductance matrix,
is a temperature-dependent thermal conductance matrix, ![]() is the temperature and vapor quality vector of grids, and
is the temperature and vapor quality vector of grids, and ![]() is the source and boundary condition vector.
is the source and boundary condition vector.
The flow chart of our proposed algorithm for solving the vector ![]() in (5) is shown in Figure 4.
in (5) is shown in Figure 4.
1) In the beginning, the thermal conductivities and power densities are stamped into the matrix. Since HTCs in two-phase liquid grids are unknown, based on the inlet condition of refrigerant, these unknown parameters are initially guessed.
2) After the MNA system is established, Super LU solver [12] is utilized to solve (5). At this iteration, the temperature profile ![]() and vapor quality
and vapor quality ![]() are renewed.
are renewed.
3) With the temperature values adjacent to the two-phase liquid grids and HTCs, each heat flux density ![]() can be computed. After that, HTCs can be updated by using the multi-linear interpolation technique with six parameters (variables) described in Section 3.1.
can be computed. After that, HTCs can be updated by using the multi-linear interpolation technique with six parameters (variables) described in Section 3.1.
![]()
Figure 4. Flow chart of the proposed algorithm.
4) With the temperature values at solid grids of silicon, the temperature dependent thermal conductance ![]() a teach solid grid of silicon is updated as described in Section 3.2.
a teach solid grid of silicon is updated as described in Section 3.2.
5) By using the homogeneous equation for pressure drop [13], the pressure of each two-phase liquid grid can be computed. By using REFPROP [14], the refrigerant temperature ![]() of each liquid grid
of each liquid grid ![]() can be obtained.
can be obtained.
6) The results obtained by 3)?5) are sent back to 2), and the whole procedure is repeated until ![]() is convergent.
is convergent.
3.1. Multi-Linear Interpolation Method for Calculating Heat Transfer Coefficients
1) Pre-build a regular table of HTCs by the interpolation method on irregular measurement data points: Directly using the measurement data points of HTCs (3899 data points) [9] to perform the interpolation for updating each HTC during the simulation flow is hard and inefficient, since the distribution of measured points is irregular and the HTC is correlated with six parameters. Therefore, we first utilize those measurement data to pre-build a regular table of HTCs.
To simply illustrate the pre-building procedure, we assume that the measurement data ![]() are correlated with two parameters
are correlated with two parameters![]() , and each
, and each ![]() is measured at
is measured at![]() . In the beginning, as shown in Figure 5, these two parameters are normalized for balancing the relation between them. Next, the desired points of the regular table are decided. After that, the normalized measured-point region is uniformly partitioned into many sub-regions. Each desired point belongs to a sub-region, and its artificial measurement is interpolated by those points inside that sub-region. The inverse distance weighting method [15] that is suitable for the irregular measured points is chosen to build the table. For example, as shown in Figure 5,
. In the beginning, as shown in Figure 5, these two parameters are normalized for balancing the relation between them. Next, the desired points of the regular table are decided. After that, the normalized measured-point region is uniformly partitioned into many sub-regions. Each desired point belongs to a sub-region, and its artificial measurement is interpolated by those points inside that sub-region. The inverse distance weighting method [15] that is suitable for the irregular measured points is chosen to build the table. For example, as shown in Figure 5, ![]() is the desired point, and its value
is the desired point, and its value ![]() can be interpolated as follows.
can be interpolated as follows.
![]() (6)
(6)
where![]() , and
, and ![]()
The interpolation form (6) indicates that the more the measured point is close to the desired point, the more its influence is. For building the regular HTC table, the formula is presented as follows.
![]() (7)
(7)
Here, ![]() is the given measurement of HTCat
is the given measurement of HTCat![]() ,
, ![]() ,
,![]() ,
, ![]() is the Euclidean distance between
is the Euclidean distance between ![]() and
and![]() , and
, and![]() .
.
2) Calculate HTCs by the multi-linear interpolation method on regular points at built HTC table: Utilizing the built regular HTC table, HTCs can be efficiently calculated by the multi-linear interpolation technique during the simulation procedure. There are many ways for solving interpolation method on regular grids, such as bilinear interpolation, bicubic interpolation, spline interpolation, etc. Here, the multi-linear interpolation on six variables is adopted.
Again, for simplicity, the same example shown in Figure 5 is used to illustrate the interpolation procedure. The value ![]() at point
at point ![]() shown in Figure 5 can be interpolated as
shown in Figure 5 can be interpolated as
![]() (8)
(8)
Here, ![]() ,
, ![]() , and
, and![]() ,
, ![]() ,
, ![]() and
and ![]() form a regular grid.
form a regular grid.
Therefore, in each iteration, the HTC at an arbitrary point e can be calculated by using the above multi-linear interpolation method with six parameters as
![]() (9)
(9)
where each ![]() is pre-established by (7), and each
is pre-established by (7), and each ![]()
![]() is equal to
is equal to
![]()
Figure 5. Illustration of the interpolation method.
![]() (10)
(10)
3.2. Temperature Dependent Thermal Conductivity of Silicon
For air-cooling or single-phase liquid cooling 3-D ICs, the gradient of temperature along z-axis (normal to the device surface) could be low. However, the refrigerant temperature is almost unchanged (in the situation, the liquid is not dried out), so the gradient of temperature along z-axis might be high in some cases. As a result, the temperature-dependent thermal conductivity should be considered. In this work, the formula of thermal conductivity versus temperature presented in [16] is used to update the thermal conductivity for the solid thermal grid.
![]() (11)
(11)
Here, ![]() is the thermal conductivity at temperature
is the thermal conductivity at temperature![]() ,
, ![]() is the thermal conductivity at temperature
is the thermal conductivity at temperature![]() , and
, and ![]() for silicon.
for silicon.
3.3. Transient Thermal Simulation
By applying the backward Euler method into (1) and (2), we have
![]() (11)
(11)
where ![]() is the constant time step,
is the constant time step, ![]() and
and ![]() are heat capacitance matrix at time step
are heat capacitance matrix at time step ![]() and
and![]() ,
, ![]() and
and ![]() are the temperature distribution at time step
are the temperature distribution at time step ![]() and
and![]() , respectively.
, respectively. ![]() is the power vector for representing equivalent power values of the control volumes at time step
is the power vector for representing equivalent power values of the control volumes at time step![]() . Since the decomposition of capacitance in two-phase grids may be changed during each iteration, re-performing LU decomposition of system matrix is needed, and the flow chart is shown in Figure 6.
. Since the decomposition of capacitance in two-phase grids may be changed during each iteration, re-performing LU decomposition of system matrix is needed, and the flow chart is shown in Figure 6.
4. Experimental Results
The proposed method is implemented in C++ language and tested on Intel Processor i7-3770 3.40 GHz CPU with 20GB RAM. Three pseudo chips with their measured data obtained by [17] are used to verify the proposed method. Meanwhile, ANSYS CFD [18], which is used to verify the simulation results, is used to verify the proposed method as well.
The structure of pseudo chips is shown in Figure 7. The thermal conductivity (W/m・K) of silicon, cover plate, and TIM are 148, 1.4, and 22 at 300 K, respectively. The
![]()
Figure 6. Flow chart of the proposed algorithm for transient simulation.
![]()
Figure 7. The geometry structure of pseudo chips.
chosen refrigerant is R236-fa. Their power maps are shown in Figures 8(a)-(c). Figure 8(a) presents the uniform power map case, its power density is 96.4 W/cm2, the inlet temperature is 304.1 K, and the mass flux is 933 kg/m2s. For the point hotspot power
map case shown in Figure 8(b), its power density is 40 W/cm2 except that the grid 34 is 202 W/cm2. Its inlet temperature is 304.1 K, and mass flux is 713 kg/m2s. The power density of row hotspot power map as shown in Figure 8(c) is 41 W/cm2 from row#1 to row#4, and 116W/cm2 in row#5 (grids 51 - 57). Its inlet temperature is 303.5 K, and mass flux is 895 kg/m2s.
The temperature comparison of col#4 between the proposed method and the measured data is shown in Figures 8(d)-(f) The blue dotted lines are the simulation results with only applying the proposed multi-linear interpolation to calculate HTCs, and the red solid lines are obtained by simultaneously utilizing the HTC interpolation technique and considering the temperature-dependent effect of silicon thermal conductivity. The results show good tendency on predicting the temperature distribution of device layers by using the multi-linear interpolation techniques on calculating HTCs during the simulation procedure. Moreover, Figure 8(d) and Figure 8(e) demonstrate that the accuracy of predicted temperature distribution can be further improved by considering the influence of temperature dependence on thermal conductivity of silicon. Figure 8(f) shows that the effect of temperature induced thermal conductivity variation might be negligible in lower temperature values.
4.1. Steady State Simulation
To further demonstrate the proposed techniques, we also implement the STEAM model with three HTC correlation functions [9] [10] [11] used in STEAM to simulate these pseudo chips. Their errors compared with ours are shown in Table 1. “HTC interpol.” represents to use the multi-linear interpolation technique for HTCs, and “HTC interpol. & TDTCS” is to simultaneously use the interpolation technique for HTCs and consider the temperature-dependent effect on thermal conductivity. Both maximum errors and average errors for all three test chips by using the proposed techniques outperform the results by using the HTC correlation functions. Our average error can be less than 7.6%, and even the maximum error is lower than 10.3% for all three test chips.
Finally, to demonstrate the robustness of the proposed method for 3-D ICs, a realistic 4-tier 3-D multiprocessor system-on-chip (3-D MPSoC) [19] is simulated. Its geometry structure is the same as Figure 1 and the total power consumption for each tier is 18.67 W. The inlet temperature is 304.1K, and mass flux is 700 kg/m2s. The error is compared with a commercial tool, ANSYS CFD. As shown in Table 1, our maximum error and average error are only 7.7% and 4.8%, respectively. Although the runtime by using the HTC correlation functions is shorter than ours, their minimum average error is twice worse than ours. Hence, the amount of accuracy improvement is more than the previous three pseudo chips. This is a very promising result, since this 3-D MPSoC is a realistic design, and it means that the proposed techniques are robust for real designs.
4.2. Transient Simulation
The case is constant workload and simulation time is 0.2 second with power density 96.4 W/cm2. Comparing with the ANSYS results, the maximum and average error of “HTC interpol.” are about 12.6% and 7.8%, and the maximum and average error of “HTC interpol. & TDTCS” are about 10.7% and 7.3%. It shows that considering the temperature-dependent effect on thermal conductivity is also important through these results and the similar trend with ANSYS result as well.
5. Conclusion
An effective and accurate thermal simulation method for two-phase liquid cooling 2-D/3-D ICs has been developed and implemented. The experimental results have demonstrated its accuracy improvement and effectiveness for the real designs.
![]()
Table 1. Error of Temperatures Compared with Thermal Sensors and ANSYS CFD.
†3-D MPSoC is compared with ANSYS CFD.
Acknowledgements
The authors would like to thank Professor Suresh V. Garimella and Professor Stefan S. Bertsch for providing the measurement data. This work was supported in part by Ministry of Science and Technology of Taiwan under Grants MOST 105-2221-E-009-168, MediaTek Inc., and Industrial Technology Research Institute.