Geospatial Area Embedding Based on the Movement Purpose Hypothesis Using Large-Scale Mobility Data from Smart Card ()
1. Introduction
As location-based sensor devices and networks have been widely spread, a large amount of mobility data of users, which can be potentially used for several research purposes, has been accumulated [1] [2] . In addition to such sensor devices, the deployment of recent infrastructure for public transit such as automated fare collection (AFC) systems with smart cards has supported the collection of large volumes of mobility data including people’s activities with detailed time and space information [3] .
Researchers have used such large amount of mobility data for the purpose of location-based recommendation such as personalization point of interest (POI) [4] . More recently, several studies have used the mobility data for regional development [5] , urban planning [6] , and policymaking [7] . One of key questions in those studies is how to model and predict people flow in a specific area where the mobility data have been collected.
Modeling and predicting people flow in a specific area results in understanding the characteristics or roles of the area by combining activity patterns of people with external information about the area [8] . Recent studies have analyzed transition patterns of people from one area to another using smart card data and characterized the areas or identified the segmentation of the areas [9] [10] . These studies solely assume that an area falls into some pre-defined demographics based on people flow in the area. However, if we regard massive transition patterns of people on an area as the context of its area, we can notice that the characteristics or roles of the area are dynamically changing according to its context of how people move on the area and for what purpose people visit the area. In other words, if two areas have similar characteristics or roles, they should have common underlying representation of areas that can be defined by such context. If we can obtain such latent representation of areas, it contributes to modeling and predicting people flow with massive mobility data more effectively and precisely.
The basic notion of representation learning [11] is that two entities are semantically similar if they are sharing common contexts; this is known as a distributional hypothesis in linguistics, which states that words that occur in similar contexts tend to have similar meanings [12] . That idea of representation learning has been recently expanded to a network embedding method [13] [14] [15] that tries to solve the problem of embedding networks into low-dimensional vector spaces by assuming that two nodes are similar if they are closely connected in a network. In the case of finding latent representation of geographical areas, if we consider areas as nodes and transition patterns of people between areas as links, we can formalize the problem of finding such representation as an extension of studying the embedding of a network. Intuitively, transition patterns of people in a business district are different from those in a residential district. Therefore, we can distinguish those different types of geospatial areas by embedding a people transition network in our low-dimensional vector spaces.
In this research, we aim to find latent representation of geographical areas using the representation learning technique. Such representation can be used for urban planning and regional development by revealing potential roles of geographical areas and their relations, which cannot be always observed from superficial information in mobility data. We can employ the notion of existing network embedding methods to find such representation from massive people flow data. However, one cannot simply apply existing embedding methods to our problem of embedding geospatial areas. For people movement in a large network of transportation systems such as railroads, several geographical constraints exist on their movement. For example, I, who live in Tokyo, do not go to Osaka to shop for daily necessities; I always buy daily necessities nearby and I don’t go all the way to far away with trivial things. Therefore we can assume that people usually tend to minimize their movements depending on their activities, given some available means of transportation at their current location. We define such geographical constraints as the “movement purpose hypothesis.” If we consider geospatial areas as a network connected with links of people with movement patterns between areas, and if we then try to embed the network in a low-dimensional vector space to obtain representations of areas, we have to consider such geographical constraints on movement of people in the real world.
In this paper, we propose a novel embedding method to obtain a vector representation of a geospatial area using movement patterns of people from large-scale smart card data. Our proposed method consists of two embedding models, which are the “concatenating model” and the “internally dividing model,” based on the movement purpose hypothesis. We conducted an experiment using massive smart card data in a large network of railroads in the Kansai region of Japan. We obtained a vector representation of each railroad station using the proposed embedding models and evaluate it in the task of multi-label classification for railroad stations. We demonstrate that our proposed models work well on actual massive mobility data from smart cards of the rail roads. Our proposed method can identify stations in a large network of railroads, which are geographically distributed but share similar characteristics or roles in the region. Therefore, we can support a city planner, a marketer, and a policy maker to design their strategies or implement their policies for regional development by providing potential characteristics of geographical areas and their relations.
Our contributions in this paper are four-fold:
1) We propose the movement purpose hypothesis and develop novel-embedding models to obtain a vector representation of a geospatial area using movement patterns of people.
2) We demonstrate that our developed models work well using actual large-scale mobility data from smart cards of the railroads in Japan.
3) We also demonstrate that our proposed models can successfully identify stations, which are geographically distributed but share similar characteristics or roles.
4) According to the results of parameter estimation of our proposed embedding model, we find that the purpose of visit for a station is 1.1 times more important than the geographical distance between stations for people movement in a large network of railroads.
2. Related Works
Our work is mainly related to mobility data analysis and network-embedding learning. In this section, we discuss our research position and novelty in relation to existing related works.
2.1. Modeling Characteristics of Geographical Areas Using Mobility Data
Recent sensor networks and infrastructures for public transit such as automated fare collection (AFC) systems with smart cards have supported the collection of large volumes of mobility data including people’s activities with detailed time and space information. In particular, mobility data from the AFC systems are currently used for several purposes such as visualization [16] , disaster prevention [17] , and service management [18] .
Moreover, aiming at several applications for location-based services including a personalized point of interest (POI) recommendation for users [4] , regional development [5] , urban planning [6] , and policymaking [7] , several studies have addressed a question of how to model people flow in a specific area and understand the characteristics of the are with such large amount of mobility data.
Recent studies have analyzed movement patterns of people from one area to another using smart card data and have characterized the areas or have enabled segmentation of the areas [9] [19] . These studies solely assume that an area falls into some pre-defined demographics based on people flow in the area. However, if we regard massive transition patterns of people on an area as the context of its area, we can notice that the characteristics or roles of the area are dynamically changing according to its context of how people move on the area and for what purpose people visit the area. In this paper, we aim at obtaining common underlying representation of areas that can be defined by such context using a embedding method. When understanding the characteristics or roles of the area, previous studies require pre-defined demographics of areas like shopping area or business district [6] [20] . On the other hand, our proposed models can learn such information from a few tagged areas using a semi-supervised learning.
2.2. Embedding of Network Data
In this research, we aim to find latent representation of geographical areas using the representation learning technique. We can employ the notion of existing network embedding methods to find such representation from massive people flow data. The network embedding method comes from graph theory and linguistics word embedding methods. In the context of the graph theory, adjacency matrix factorization techniques like singular value decompositon (SVD) and non-negative matrix factorization (NMF) are the prototype [21] . On the other hand, word embedding methods have been recently advanced. The basic notion of word embedding is that two entities are semantically similar if they share common contexts; this is known as distributional hypothesis in linguistics, which states that words that occur in similar contexts tend to have similar meanings [12] [22] . Some works tried embedding network graph structure directly [13] [14] [15] . These network-embedding methods are useful in many tasks such as visualization, node classification, and link prediction [23] .
Network embedding has been further developed for time series analysis [24] and for heterogeneous network [25] . The predictive text embedding (PTE) method for heterogeneous network embedding, which can embed words, documents, and labels to a low-dimensional vector space. The PTE method embeds these three different heterogeneous networks to a same vector space and obtain vectors with a semi-supervised learning style. Our proposed models also use three heterogeneous networks, but it embeds them to two different vector spaces, the geospatial vector space and the role vector space. We describe this in more detail in the following section.
3. Method
This section first describes the “Movement Purpose Hypothesis” which the people flow is caused from geolocation and purpose. Next we explain how the network form from massive people flow and the necessity of label propagation on the network. We extend propagating labeled network embedding model for massive people flow data. Finally, we propose models based on the hypothesis and explain precisely.
3.1. Movement Purpose Hypothesis
We propose the “movement purpose hypothesis,” as shown in Figure 1 for people flow data such as the GPS data, the cell phone base station data, the train travel data, etc. We apply the train travel records as the people flow data on the Japan Kansai region extracted from the smart card system in this paper. So, we represent an area as a station in the figure. This hypothesis presumes that a person moves somewhere to accomplish a purpose that the person cannot accomplish there. In other words, the movements of people (People flow) are represented as the sum of the geographical proximities between areas (Geographical constraints) and the role of the area (Purpose proximity). This model describes that people move to a nearby location, which means a destination to realize their purposes, from the present location. As accumulating thus people’s location and desire, the people flow network is shaped (Figure 1 right). On the other hand, we propose that the people flow regards as the sum of the amount of geolocation data and the amount of purpose data. In Figure 1, we illustrate that two networks (the geographical constraints network and the purpose network) generate the massive people flow network. And we think that thus three networks’ relationship depends on the distance on the latent vector representation.
There are three graphs that do not mutually share their vectors, the people flow graph (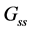 ), the geographical constraints graph (
), the geographical constraints graph (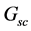 ), and the purpose proximity graph (
), and the purpose proximity graph (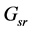 ). More specifically, a vector representation in each graph is the following:
). More specifically, a vector representation in each graph is the following: 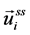 for all vertices
for all vertices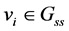 ,
, 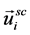 for all vertices
for all vertices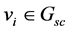 , and
, and 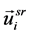 for all vertices
for all vertices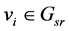 . The model shown in the Figure 1 hypothesis leads to the following equation, which is established among vectors.
. The model shown in the Figure 1 hypothesis leads to the following equation, which is established among vectors.
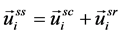 (1)
(1)
![]()
Figure 1. Schematic showing the “movement purpose hypothesis” and proposed models.
We interpret this equation as two types: “concatenating model” and “internally dividing model.” For the “concatenating model,” we interpret the operator “+” as connecting two vectors and producing a new vector with dimensions that are twice as numerous as the number of dimensions of each vector, not that we add each element in the two vectors (Figure 1, concatenating model). Furthermore, for the “internally dividing model,” we interpret the Equation (1) as the people flow graph node (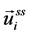 ) locates between the geographical constraints graph node (
) locates between the geographical constraints graph node (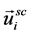 ) and the purpose proximity graph node (
) and the purpose proximity graph node (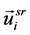 ) (Figure 1, internally dividing model). We explain these two models more in the following subsections.
) (Figure 1, internally dividing model). We explain these two models more in the following subsections.
3.2. Concatenating Model
Based on the concatenating model, vector representations are acquired by the learning algorithm shown in Table 1. This algorithm needs the geographical constraints network (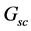 ), the purpose proximity network (
), the purpose proximity network (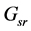 ), the people flow network (
), the people flow network (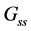 ), the number of sampling (T), the initial learning rate (
), the number of sampling (T), the initial learning rate (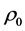 ), the number of negative sampling (K), and the dimension of the embedding (d) as input. We apply the network embedding model called the “LINE (2nd) model” proposed by Tang et al. [15] . This model approximates second-order proximity between two vertices, optimizing each representation vector. The objective function is as follows:
), the number of negative sampling (K), and the dimension of the embedding (d) as input. We apply the network embedding model called the “LINE (2nd) model” proposed by Tang et al. [15] . This model approximates second-order proximity between two vertices, optimizing each representation vector. The objective function is as follows:
![]() (2)
(2)
In this equation, ![]() indicates the empirical edge weight from the vertex
indicates the empirical edge weight from the vertex ![]() to the vertex
to the vertex![]() .
. ![]() which is the transition probability from
which is the transition probability from ![]() to
to ![]() is estimated using the embedding vector
is estimated using the embedding vector ![]() of the vertex
of the vertex ![]() and the context vector
and the context vector ![]() of the vertex
of the vertex ![]() as following:
as following:
![]() (3)
(3)
We set this objective function for three networks individually and derive update
![]()
Table 1. Learning algorithm of the concatenating model.
equations by differentiating them with respect to the each vertex vector (![]() ) and the each context vector (
) and the each context vector (![]() ). We acquire vertex vector sequentially (Lines 7, 11 and 14) based on the concatenating model (Lines 8 and 12) using this SGD style learning algorithm.
). We acquire vertex vector sequentially (Lines 7, 11 and 14) based on the concatenating model (Lines 8 and 12) using this SGD style learning algorithm.
3.3. Internally Dividing Model
For the “internally dividing model,” the node vector in the people flow graph (![]() ) locates between the geographical constraints graph node vector (
) locates between the geographical constraints graph node vector (![]() ) and the purpose proximity graph node vector (
) and the purpose proximity graph node vector (![]() ) as the following equation.
) as the following equation.
![]() (4)
(4)
This equation models that people decide the destination place in consideration of both the physical place relation and the purpose they want to accomplish there.
We set the objective function as in the Equation (2) for each graph. However, when updating the vector ![]() in
in![]() , the vector
, the vector ![]() depends on the vector
depends on the vector ![]() and the vector
and the vector ![]() through the Equation (4). Therefore, it is necessary to derive new update rules for the vectors and the parameter
through the Equation (4). Therefore, it is necessary to derive new update rules for the vectors and the parameter![]() . For the objective function
. For the objective function ![]() with the people flow graph (
with the people flow graph (![]() ), we carefully differentiate all dependent variables (
), we carefully differentiate all dependent variables (![]() ) and parameter (
) and parameter (![]() ). We can derive the following update rules for the people flow graph. Due to the lack of space, we show the updating equations about vertex vectors and
). We can derive the following update rules for the people flow graph. Due to the lack of space, we show the updating equations about vertex vectors and![]() .
.
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
In these equations,![]() . We also apply the joint training style same as the PTE (joint) method [25] .
. We also apply the joint training style same as the PTE (joint) method [25] .
4. Data Description and Input Arrangement
As described in this paper, our proposed models need three networks: the people flow network, the geographical constraints network and the purpose proximity network. To arrange these three networks as input, we apply three datasets for the experiment. In this section, we explain these three datasets and the arrangement.
Getting on and off dataset for the people flow network: This dataset includes massive smart card data for the Japan Kansai region (southwestern half of Japan, including Osaka). This dataset has passenger’s smart card log provided by six railway companies. The providers have anonymized this dataset. The dataset contents mainly consist of six elements: each user of the gender, age, getting on and off date and time, and boarding and destination station. The summary of this dataset is shown in Table 2. We make the people flow network using this dataset, which is people getting on and off a train between two stations. This is a directed graph and the weight of each edge is P(destination station|boarding station). We select only weekday morning movement data from 7 AM to 10 AM in April, 2013 to capture the purpose of going to work in the morning.
Train route map dataset for the geographical constraint: This time, we apply the train network information as geographic proximity information obtained through the Japan train line API1. We construct the train route map through this. The graph is undirected and the weights of all edges are equal and the route map is shown in Figure 1 left (geographical constraints).
Purpose of use dataset for the purpose proximity network: This paper is intended to estimate each station’s role. As described herein, we produce a dataset using the results of the person trip survey. In Japan, the Ministry of Land, Infrastructure and Transport takes a nationwide survey through questionnaire from many persons every decade. We apply the 2010 results2 to our experiment, which includes how much people come to each station for what purpose. The purposes of the getting off each station are “commuting to work”, “commuting to school”, “going home”, “on business”, and “others”. A summary of this dataset is shown in Table 3. We make the station-purpose graph as the purpose proximity network from this dataset which presents a probability distribution of purposes to go to a station. This graph is undirected. When making the
![]()
Table 2. Overview of the getting on and off dataset.
![]()
Table 3. Summary of the purpose of use dataset.
people flow network, we select only weekday morning data. So, we do not use the a “going home” purpose in this dataset and use the remaining four purposes, because we think that most people do not return home in the morning.
5. Experiment and Results
In this section, we evaluate the effectiveness of the developed models for geospatial data. For this purpose, we compare various algorithms and conduct an experiment. As reported below, we describe the results.
5.1. Experimental Procedure
As described in this paper, we conducted a multi-label classification experiment because the purposes of dropping off passengers at a station are plural. To be exact, purposes will differ from person to person. We regard a station as a probability distribution of some purposes and estimate it in the experiment.
The experimental procedure is the following. First, obtaining the vector representation using the listed methods in Section 5.2. Second, the training classifier for each experiment using training labeled data set made from a part of the purpose of use dataset. Finally, we conduct a prediction evaluation using test data produced from the rest of the dataset and evaluate the obtained result using some measurements.
For multi-label classification, we use a multiclass logistic regression classifier. We use the LIBLINEAR package3 as the classifier. We use three measurements for the multi-label classifications, which are the “KL divergence”, the “Mean Reciprocal Rank” (MRR), and the “Mean Average Precision” (MAP). For this experiment, the number of classes is four described in Section 4. We evaluate the method accuracy using two cross- validations randomized five times repeatedly. In other words, we use all the getting on and off data for obtaining vector representations, but we use only half of the stations in the purpose of use dataset for obtaining vector representations and classifier training. We use the rest to evaluate the classifier accuracy. We repeat this experiment procedure five times by randomizing the purpose of use dataset.
Finally, we evaluate geographical locations around each purpose vector. The evaluation metric is the average value of the standard deviation of the actual geolocation of stations near the purpose label vector. Because, when the average of the standard deviation of the nearby station of the purpose label is large, the station group is extracted for the purpose of the station without geographical constraints.
5.2. Compared Algorithms
We use the following methods to compare algorithms.
1) Weighted random: random sampling from a discrete probability distribution. In advance, we calculate each purpose distribution from a training dataset. When predicting the purpose of dropping off at a station in test data, the method predicts it by selecting a purpose randomly according to the arbitrary distribution.
2) Word2Vec [12] : Word2Vec is an efficient word embedding model that learns the representation of each word in a large corpus. We simply use the Skip-gram model in this experiment.
3) GloVe [26] : GloVe is another efficient word embedding model. The method uses global word-word co-occurrence statistics from a corpus to learn word representation vectors.
4) DeepWalk [14] : DeepWalk is the first network embedding method which can learn the representation of networks. This model only works for an unweighted graph. For each vertex, truncated random walk is used to translate the graph structure into linear sequences.
5) LINE [15] : LINE is the other network embedding method. LINE defines the first proximity and the second proximity between vertices using edge weight information. It obtains the representation by approximating the inner product value between the vertex and context vector to each proximity (LINE(1st) and LINE (2nd)). The LINE will achieve the best performance when concatenating the representation the first proximity and the second proximity (LINE(concat)).
6) PTE [25] : PTE is the network embedding method for a heterogeneous network. This method applies to three different networks which are the word-word, word- document, and word-label networks. They propose two learning styles, which are “pre- train” and “joint” learning style. We select “joint” learning style, which is slightly better than pre-train learning style in their report (PTE(joint)). This method can embed vertices in three network graphs to same vector spaces. The same node in different graphs has the same vector representation among all graphs.
7) Proposed: Our proposed models are all for learning geospatial area embedding through large-scale mobility data from smart cards. We offer two models based on the “Movement Purpose Hypothesis” described in the Section 3.1, which is the concatenating model (“concat”) and the internally dividing model (“divide”). Our proposed models can embed vertices in three network graphs to different vector spaces. A single node in different graphs has different vector representations with each graph (![]() ).
).
Word2Vec and GloVe are necessary for sentences as input information because of word embedding methods. We regard the sequence of stations which is history of each user getting on and off as a sentence. Word2Vec, GloVe, DeepWalk, and LINE methods are unsupervised style learning. Therefore, we merely apply user information related to getting on and off at different stations for training. PTE and our proposed models are semi-supervised style learning. We set the people flow network as the word- word network, the geographical constraints network as the word-document network, and the purpose proximity network as the word-label network. On all method, the dimension of the node vector is set as 200, but in the proposed concatenating model, ![]() has twice the number of dimensions: 400.
has twice the number of dimensions: 400.
5.3. Results
This section presents the performance and characteristics of our proposed models.
5.3.1. Performance of Multi-Label Classification
Table 4 shows the performance of multi-label classification. One can start with a comparison of weighted random with others. Except for weighted random, all other methods are embedding word or node to vector space. In the KL divergence metric, all other methods are superior to the weighted random method. In other metrics, all other method results are equal to or better than the weighted random method. Therefore, applying embedding method to the people flow data is reasonable and efficient to extract the purpose distribution for each station.
Next, we compare the performance of GloVe with others. GloVe indicates the best result at the KL divergence metrics because only GloVe uses global co-occurrence information in the dataset. The effect of long context co-occurrence information also shows the result between LINE (1st) and LINE (2nd). Although LINE (1st) directly approximates the edge weight between two nodes, LINE (2nd) approximates two hops sharing node proximity. This effect appears in the KL divergence and the MRR result. These results indicate that using the global graph structure is good for multi-label classification.
We compare our proposed models with the PTE (joint) method. Particularly, the proposed model of (divide![]() ) is superior to the PTE method in point of the KL divergence and the MRR metrics. Moreover, proposed (concat
) is superior to the PTE method in point of the KL divergence and the MRR metrics. Moreover, proposed (concat![]() ) is also superior in terms of the KL divergence and the MAP metrics. These results indicate that our proposed models use labeled information more efficiently than PTE (joint) method on the people flow data.
) is also superior in terms of the KL divergence and the MAP metrics. These results indicate that our proposed models use labeled information more efficiently than PTE (joint) method on the people flow data.
Finally, we make a comparison of our proposed models. The proposed (divide![]() ) is superior to the proposed (concat
) is superior to the proposed (concat![]() ) concerning the KL divergence and the MRR metrics. This difference derives from the update style difference between the two models. The concatenating model is updating half of vector element once, but the internally dividing model is updating all vector elements. This difference appears to learned vector representations. We describe this difference in greater detail in the following sections. In both models,
) concerning the KL divergence and the MRR metrics. This difference derives from the update style difference between the two models. The concatenating model is updating half of vector element once, but the internally dividing model is updating all vector elements. This difference appears to learned vector representations. We describe this difference in greater detail in the following sections. In both models, ![]() results are superior to
results are superior to ![]() and
and ![]() models results, which shows that it is necessary to both the geospatial information and the purpose information for the multi-label classification.
models results, which shows that it is necessary to both the geospatial information and the purpose information for the multi-label classification.
Regarding ![]() estimation result in the proposed (divide) model, we show the result in Table 5. This result indicates that
estimation result in the proposed (divide) model, we show the result in Table 5. This result indicates that![]() , which means that
, which means that ![]() is more important than
is more important than![]() .
.
5.3.2. Geographical Locations around Each Purpose Vector
Next, it is necessary to unveil the obtained purpose vector characteristics. Therefore, we inspect stations around each purpose vector. As described in this paper, we attempt to extract purposes of a station to go accurately and the purposes of a station are irrelevant to the geospatial location of the station. If so, our proposed method will gather distant stations one after another around a purpose vector. We evaluate this hypothesis to
![]()
Table 4. Results of multi-label classification. The KL divergence is better if it is a smaller value. Other metrics are all better if larger values.
![]()
Table 5. Estimation result of α parmeter.
confirm the standard deviation of station geolocation. The result is presented in Table 6. This table is the standard deviation of station geolocation around each purpose vector in 10 nearest stations.
Comparison of the proposed (divide![]() ) model with the PTE(joint) method shows that the proposed (divide
) model with the PTE(joint) method shows that the proposed (divide![]() ) standard deviations are larger than the PTE(joint) one for all purposes. This shows that the proposed (divide
) standard deviations are larger than the PTE(joint) one for all purposes. This shows that the proposed (divide![]() ) model can gather distant stations around each purpose node. The proposed (concat) results have a smaller standard deviation than other methods have. In the following visualization result section, we consider the results in greater detail.
) model can gather distant stations around each purpose node. The proposed (concat) results have a smaller standard deviation than other methods have. In the following visualization result section, we consider the results in greater detail.
5.3.3. Visualization of Vector Representation
Finally, we present an illustrative visualization of each method. We present a visualization in Figure 2. Because of space limitations, we select six methods of visualization. In the figure, each point represents a station or a purpose. Then they are colored by six train companies. In the figure, (a) and (b) are past works and (c)-(f) are our proposed method visualizations.
The (a) DeepWalk vector forms clusters gathering at each company. In this people flow dataset, we found from statistically results that most people usually move in a small area and they do not transfer so much. Therefore, the DeepWalk visualization result is reasonable because it captures local context information. This result also shows (e) proposed (divide![]() ). Linearly aligned stations are apparent in the figure, showing that these stations are along the same train line.
). Linearly aligned stations are apparent in the figure, showing that these stations are along the same train line.
In (f) proposed (divide![]() ), the visualization result is mixed with six companies around purpose vectors. And (d) proposed (divide
), the visualization result is mixed with six companies around purpose vectors. And (d) proposed (divide![]() ) is the sum of (e) proposed (divide
) is the sum of (e) proposed (divide![]() ) and (f) proposed (divide
) and (f) proposed (divide![]() ). By this representation, this method gathers distant stations around each purpose vector and achieves a useful purpose estimation result in MAP metric on Table 4.
). By this representation, this method gathers distant stations around each purpose vector and achieves a useful purpose estimation result in MAP metric on Table 4.
6. Discussion and Summary
As described in Section 5.3, our proposed models achieve better results than the PTE
![]()
Table 6. Standard deviation of station geolocation around each purpose vector (Nearest@10).
![]()
Figure 2. The obtained vector visualization by t-SNE [27] toolkit. It is noteworthy that each point represents a station or a purpose. They are colored according to train companies.
method. These results indicate that, for large-scale movement data, which have spatial dependence, the proposed models capture the characteristics of the purpose of each area better than the PTE method does. People’s moving areas are usually small. They live in defined areas. In light of this constraint, our proposed models work better than the PTE method. For the multi-label classification task, our proposed models (concat ![]() and divide
and divide![]() ) show good results in Table 4. This result underscores the correctness our proposed “Moving Purpose Hypothesis.” Especially for vector visualization results (Figure 2), the proposed (divide) models decompose each area to geolocation dependency vectors and purpose vectors. Finally, the
) show good results in Table 4. This result underscores the correctness our proposed “Moving Purpose Hypothesis.” Especially for vector visualization results (Figure 2), the proposed (divide) models decompose each area to geolocation dependency vectors and purpose vectors. Finally, the ![]() parameter estimation result is impressive. This result means that the purpose is 1.1 times more important than the distance. Therefore, people move to distant places when they have a purpose that they actively want to complete.
parameter estimation result is impressive. This result means that the purpose is 1.1 times more important than the distance. Therefore, people move to distant places when they have a purpose that they actively want to complete.
However, the currently proposed models’ performance is slightly better than unsupervised embedding methods because our proposed models use only two-hop proximity, and they do not capture the global network structure. As the next step, we should consider a graph global structure with the heterogeneous network and how to apply the labeled network more efficiently. The graph global structure can be captured by the GraRep [13] or GloVe [26] . It is necessary to refer to such approaches for extracting purposes to go to an area.
We believe that there is considerable research room to representation learning for the geospatial network.
NOTES
![]()
1http://www.ekidata.jp/.
2https://www.kkr.mlit.go.jp/plan/pt/data/pt_h22/index.html.
![]()
3https://www.csie.ntu.edu.tw/~cjlin/liblinear/.