1. Introduction
Newton’s law of gravity is the cornerstone of many disciplines in space technology, astronomy and cosmology, but so far no acceptable theory to explain its peculiarities is existing. It is broadly accepted that any suitable theory should include, or will be a merger of, classical quantum theory and general relativity [1] [2] . The main problem is, however, that the basic equations of quantum mechanics and relativity are not in correspondence. This fact is most easily seen that, when the common factor in the Dirac equation and the Schrödinger equation are used to combine both, a contradiction shows up. The reason for this contradiction is that relativity requires co-variance throughout where the Schrödinger equation is not co-variant. There are examples where this contradiction is circumvented like in the theory of the magnetic moment of particles, leading to the spins. In the present paper, a new scheme of analysis is presented for the mutual interaction between particles that have some exchange with respect to time and space. The specific requirements on invariance and co-variance of operators and quantities will be carefully taken care of and are finally found to be of great importance for the result. This pair formation is described quantum mechanically, either starting from the classical Schrödinger equation or the relativistic Dirac equation. This latter is formulated in a quantum mechanical setting. Both result in the same wave function describing pairs of particles. Since this wave function represents a pair potential, a relativistic mass can be attributed to it which is used in the Dirac equation to derive an interaction field between the members that form the ensemble. It is found that the right form of Newton’s gravity law emerges by consequently working through the proposed schemes of both quantum mechanics and the basic equations of relativity theory as expressed by the Dirac equation1.
2. Forming of Pairs
Starting point is the assumption that there are two independent particles indicated by the masses mi and mj which are described by the normal Schrödinger equation. In the present treatment the kinetic energy is taken into account and they experience some force reflected by the potential Vi and Vj. Spherical symmetry is next adopted and the only boundary condition is that the wave function is zero at infinity. An observer at mi at a distance rij from particle mj and another on mj at rji from particle mi will see that the total wave equation is defined as follows [5] :
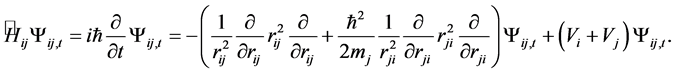 (1)
(1)
where 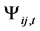 is the time and space dependent wave function. The time dependence can be removed by replacing the time dependent wave function
is the time and space dependent wave function. The time dependence can be removed by replacing the time dependent wave function 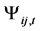 by
by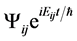 . Further define
. Further define 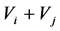 by
by 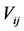 and we get:
and we get:
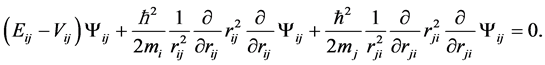 (2)
(2)
To simplify the equation replace 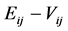 by
by 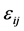 to propose a solution that is valid in areas where the Vij is not of great influence anymore as follows:
to propose a solution that is valid in areas where the Vij is not of great influence anymore as follows:
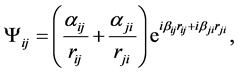 (3)
(3)
where 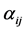 and
and 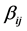 are constants independent of space coordinates and time. This solution means that we consider the wave function outside the surroundings where the potential energy with all its peculiarities has a very minor effect on the shape of the wave function. The only interaction that can play a role will then be based solely on gravitational interaction. By substituting the solution in Equation (3) the following relation is found:
are constants independent of space coordinates and time. This solution means that we consider the wave function outside the surroundings where the potential energy with all its peculiarities has a very minor effect on the shape of the wave function. The only interaction that can play a role will then be based solely on gravitational interaction. By substituting the solution in Equation (3) the following relation is found:
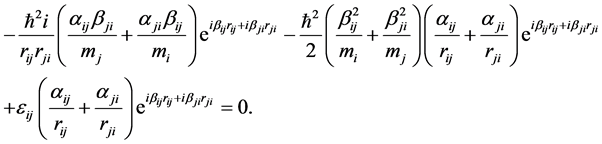 (4)
(4)
The first term at the left hand side is to be set to zero so that in a pair-wise process 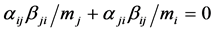 and
and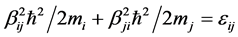 .
.
At the moment not much is known about the α's, but one requirement to be imposed on the wave function is that it represents a pair of particles. For the time being it can be said that:
a) The α's cannot depend on the running variables in the wave equation: rij or t. It will be a constant that can only depend on fundamental nature constants and the particle masses.
b) It should make no difference for the outside world how one member sees its partner or whether and how we see the two members of the pair. It means that most likely we can say: 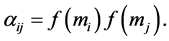
c) There is no pair if either mi or mj equals zero so that 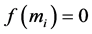 for
for ![]()
Later it will be found that, for the sake of symmetry in the mutual gravitational interaction, the two α's should be equal. It also means that the β’s have opposite signs and fixed values and by taking the α's equal we make their values independent of the masses and the energies of the members of the pair. The ![]() could have been split into two separate quantities as
could have been split into two separate quantities as ![]() and
and ![]() to dedicate the
to dedicate the ![]() and
and ![]() -values to the separate energies of the two particles. It is also interesting to notice that the solution of the wave equation for the pair looks different from a solution for a single particle:
-values to the separate energies of the two particles. It is also interesting to notice that the solution of the wave equation for the pair looks different from a solution for a single particle:
![]() . (5)
. (5)
For instance if we take a look at the ri dependence in the solution (3) we see that there is an extra r2 dependent factor in the exponential term. This latter term is insufficient to make such a solution applicable for the operator working on r2. For it to be sufficient we need the total pre-exponential factor as given in Equation (3).
Another approach is taking the Dirac equation as the starting point. In this way, we guarantee full co-variance throughout the entire analysis. The Dirac equation reads [6] :
![]()
or expressed alternatively:
![]() ,
,
and translated into quantum mechanical language for an ensemble of two particles:
![]() (6)
(6)
where ![]() is the momentum operator to be written out in spherical coordinates as in Equation (1) and mi,o the rest mass of the particle i in the ensemble ij. Also in this case it immediately can be seen that, with the solution of the form as in Equation (3), the same interpretation as before can be given.
is the momentum operator to be written out in spherical coordinates as in Equation (1) and mi,o the rest mass of the particle i in the ensemble ij. Also in this case it immediately can be seen that, with the solution of the form as in Equation (3), the same interpretation as before can be given.
For the α's it means that:
d) If the energy of the ensemble should be related to the masses of each member, which definitely is the case outside the area where the potential energy is not of any importance, it follows that: ![]() and a similar equation in the case that the Dirac equation is taken as starting point. It means, following the other boundary condition
and a similar equation in the case that the Dirac equation is taken as starting point. It means, following the other boundary condition![]() , that
, that![]() . This is in accordance with the argument given in point b). For the transparency of the analysis, we will, however, not yet take into account that the α's are equal. Leaving the statement of the equality of the
. This is in accordance with the argument given in point b). For the transparency of the analysis, we will, however, not yet take into account that the α's are equal. Leaving the statement of the equality of the ![]() values for later has an interesting, causality related, consequence on the symmetry of the gravitational interaction between particles.
values for later has an interesting, causality related, consequence on the symmetry of the gravitational interaction between particles.
It appears that with the simple assumption of having a pair of particles, and taking a wave equation with spherical symmetry, a solution is obtained that, apparently, couples the particles into pairs. It is surprising that the procedure only works well with sets of two particles.
The wave function as derived gives the presence of an entity for which it is derived. In this case it is the pair potential so that a mass can be dedicated to this potential defined as ![]() and which becomes equal to:
and which becomes equal to:
![]() . (7)
. (7)
As said before, in this expression the ![]() which occurs in the Dirac equation can be identified as a quantity that represents the presence of a pair of particles. It is related to the mass of the pair since the product of the complex conjugated wave function and the wave function with the appropriate operator, in this case the
which occurs in the Dirac equation can be identified as a quantity that represents the presence of a pair of particles. It is related to the mass of the pair since the product of the complex conjugated wave function and the wave function with the appropriate operator, in this case the![]() , gives the expectation value of the operator. The α-values in this last equation accommodate the influence of this
, gives the expectation value of the operator. The α-values in this last equation accommodate the influence of this ![]() but, as it follows from
but, as it follows from ![]() with
with ![]() that there is some freedom in choosing its dependence on relativistic parameters such that the right hand side of Equation (7) becomes an invariant as it should be.
that there is some freedom in choosing its dependence on relativistic parameters such that the right hand side of Equation (7) becomes an invariant as it should be.
3. Relativistic Interaction
Now, as a next step, the pair is considered as essentially one entity and the problem can be analysed in the relativistic four dimensional space where the Dirac equation is the appropriate starting point [1] [6] :
![]() or
or![]() .
.
Again we will have to translate this equation into the appropriate quantum mechanical language for pairs as one entity and therefore make the following transformations:
![]() ,
,
and
![]()
The last expression is, as different from earlier, a mixed sum of the momenta. This representation is a consequence of the fact that the particles have been treated only in pairs and that spherical symmetry remains to be adopted. Referring to Figure 1 the total relativistic Dirac equation for an undefined number of pairs (ij) is set up. There are ![]() particles which make a total of
particles which make a total of ![]() = N!/(2(N − 2)!) pairs, each of which are described by a wave function as a solution of the initial Schrödinger equation. As before the α-values accommodate all necessary multiplication constants. Adding up for all pairs and treating them as mutually independent and taking into account the basic rules of quantum mechanics, lead to:
= N!/(2(N − 2)!) pairs, each of which are described by a wave function as a solution of the initial Schrödinger equation. As before the α-values accommodate all necessary multiplication constants. Adding up for all pairs and treating them as mutually independent and taking into account the basic rules of quantum mechanics, lead to:
![]() (8)
(8)
As before the time dependences can be removed by setting:
![]() (9)
(9)
so that:
![]()
Figure 1. Forming and describing of ![]() pairs.
pairs.
![]() (10)
(10)
If all α's would have been equal to zero, a propagating wave ![]() extending in the radial direction with the light velocity would have resulted. Non zero values of
reduce this speed and, as a consequence, give mass to the field
extending in the radial direction with the light velocity would have resulted. Non zero values of
reduce this speed and, as a consequence, give mass to the field![]() . The proposed solution will be:
. The proposed solution will be:
![]() , (11)
, (11)
which is inserted into:
![]() (12)
(12)
From the boundary condition that ![]() for
for ![]() to infinity a fifth condition on the α's can be derived:
to infinity a fifth condition on the α's can be derived:
e) ![]() is negative under all circumstances.
is negative under all circumstances.
Putting all five conditions on ![]() together we can already conclude that the explicit expression for it is:
together we can already conclude that the explicit expression for it is:
f) ![]() with n equal to 1, 2 etc.
with n equal to 1, 2 etc.
Now, some algebra needs to be done, but in order to redistribute the various contributions it is easiest to start from the simplified equation:
![]() (13)
(13)
with the solution proposed in Equation (11) it can immediately be seen that the sixth term in the first line is equal to the right hand side.
At this point a remark has to be made: removing the term ![]() means that some basic interaction occurs between the gravitational field and the particle. Obviously, for this separate term, a Dirac equation can be formulated that shows that an entity with some relativistically derived mass operates and leaves behind a contribution to the interaction energy in the Equation (13). So already at this point there is direct interaction between the pair and the field around. Also removing the sixth term left together with the only remaining term at the right means that there is third interaction between the fields and the pair.
means that some basic interaction occurs between the gravitational field and the particle. Obviously, for this separate term, a Dirac equation can be formulated that shows that an entity with some relativistically derived mass operates and leaves behind a contribution to the interaction energy in the Equation (13). So already at this point there is direct interaction between the pair and the field around. Also removing the sixth term left together with the only remaining term at the right means that there is third interaction between the fields and the pair.
Taking all these interactions into account it is seen that all α-terms in Equation (12) have disappeared. This has a profound meaning: in this model gravity is due to second order effects of peculiarities of the spherical symmetry in a relativistic setting. The effect is weak and operates over a long range so:
![]() (14)
(14)
The contributions can now be redistributed, but first multiply all terms by ![]() and observe that the proposed solution is the only one that gives a sharp value for the quantity
and observe that the proposed solution is the only one that gives a sharp value for the quantity ![]() and
and![]() :
:
![]() (15a)
(15a)
![]() (15b)
(15b)
Cutting the Equation (14) into two separate ones as given in Equations (15a) and (15b) looks like arbitrary, as any cut between terms can be made, but if we now come back to the original suggestion as made in f), we a see that the gravitational interaction becomes symmetric. The gravitational energy of particle i is equal to the gravitational energy of particle j. It also reflects the point that a pair has to be seen as one entity. The observer cannot distinguish between the separate members of the pair.
It is also important to notice that the operators ![]() and
and ![]() commute. It means that “Er” is the quantity that has a sharp value, meaning that E has a sharp value if r is well defined.
commute. It means that “Er” is the quantity that has a sharp value, meaning that E has a sharp value if r is well defined.
4. Law of Gravity
Most important for finding out how the members of a pair see each other is to look at the Equations (15a) and (15b) by an observer on mi who sees the particle mj at a distance of rij and an observer on particle mj looking at mi from a distance rji. Both see each other from the same distance ![]() and they already know that
and they already know that![]() . There are no operators anymore in Equation (15), and they can conclude that
. There are no operators anymore in Equation (15), and they can conclude that![]() . This is an important conclusion. Obviously an electron and a proton forming a pair will have mutual interactions which are the same although their masses differ by some factor of about 1800 [7] . The result is a simple relation:
. This is an important conclusion. Obviously an electron and a proton forming a pair will have mutual interactions which are the same although their masses differ by some factor of about 1800 [7] . The result is a simple relation:
![]() (16)
(16)
The boundary condition is that ![]() goes to zero for r to infinity so that
goes to zero for r to infinity so that![]() , and because both particles in the pair change their energy by the same amount. It follows for the two members of the ensemble together that:
, and because both particles in the pair change their energy by the same amount. It follows for the two members of the ensemble together that:
![]() (17)
(17)
and the gravitational force is given by: ![]()
All the work done to describe the total gravitational force, or rather the potential energy, has been based on the idea that all pairs that have been formed are acting independently so that we can add all the contributions of different masses constituting bodies in the real world without any interference.
Now it is important to see how pairs consisting of particles of different masses present themselves in![]() . As a consequence of Einstein’s law that the rest energy of a particle is proportional to its mass which is also a direct consequence of the fact that the pairs which gives gravitational interaction are acting as single entities, and in view of Equation (17) we can only conclude that the exponent n in condition f) is equal to one. As a consequence of the result in this equation the attractive force between two particles is proportional to the product of the two interacting masses. It also follows that due to gravitational interaction which carries energy, and for which a separate Dirac equation can be set up, some mass, although not much, is attributed to the pairs.
. As a consequence of Einstein’s law that the rest energy of a particle is proportional to its mass which is also a direct consequence of the fact that the pairs which gives gravitational interaction are acting as single entities, and in view of Equation (17) we can only conclude that the exponent n in condition f) is equal to one. As a consequence of the result in this equation the attractive force between two particles is proportional to the product of the two interacting masses. It also follows that due to gravitational interaction which carries energy, and for which a separate Dirac equation can be set up, some mass, although not much, is attributed to the pairs.
The final result is:
![]() (18)
(18)
Referring to Figure 2 where two masses M1 and M2 have particles numbered as m1j and m2k form N1 ´ N2 pairs described by ![]() in which each kl-combination contributes separately to the interaction energy. Adding up all the interactions between
in which each kl-combination contributes separately to the interaction energy. Adding up all the interactions between
particles, which in principle see each other at different distances which is a problem that has already been solved in the formulation of the classical theory of electrostatics [8] .
Finally, Newton’s gravitation law is obtained which reads: ![]() in which
in which ![]() is defined as a gravitational field around an entity constituting a space coordinates dependent mass density
is defined as a gravitational field around an entity constituting a space coordinates dependent mass density![]() . G is the well known gravitational constant equal to: 6.673 ´ 10−11 m3∙kg−1∙sec−2.
. G is the well known gravitational constant equal to: 6.673 ´ 10−11 m3∙kg−1∙sec−2.
In accordance with the theory of electrostatics the gravity law can also be given in vector representation for bodies M1 and M2 which have their centres of gravity at a separation of R:
![]() (19)
(19)
From Equations (18) and (19), an explicit expression for the parameter ![]() can be derived and also, with the help of Equations (11) and (12), the small mass to be attributed to the gravitational interaction can be found.
can be derived and also, with the help of Equations (11) and (12), the small mass to be attributed to the gravitational interaction can be found.
5. Discussion
Without claiming anything about the validity or the consequences of the model proposed, a simple straightforward model on the mutual interaction between two particles that influence the surrounding field leads elegantly to the right description of the gravitational interaction between two masses.
First, the Schrödinger equation is set up for two particles where the only assumption is that they are there and that the wave equation will have purely spherical symmetry. Surprisingly this is a solution that leads to the forming of pairs, in which only two particles are participating. One particular particle can form pairs with all others present, but each pair has to consist of two individual particles. The pair density probability, given by the wave function, is then used to substitute for the relativistically invariant entity, ![]() , in the Dirac equation [1] [6] . It has been shown that the Dirac equation can be taken in the first calculation as well so that the whole analysis would be based on co-variant equations. This would lead to the same form of the probability density, although with different constants, but it creates no problems when allocating the mass dependences to the α's.
, in the Dirac equation [1] [6] . It has been shown that the Dirac equation can be taken in the first calculation as well so that the whole analysis would be based on co-variant equations. This would lead to the same form of the probability density, although with different constants, but it creates no problems when allocating the mass dependences to the α's.
Replacing the quantities in the Dirac equation by the appropriate operators, and again taking purely spherical symmetry, it is found that a solution is only possible when the interaction energy of the pair is proportional to the inverse of the distance between them. It is important consider that the operators ![]() and
and ![]() commute. It means that “Er” is the quantity that has a sharp value, meaning that E has sharp value if r is well defined.
commute. It means that “Er” is the quantity that has a sharp value, meaning that E has sharp value if r is well defined.
After adding up the effects the appropriate form of the classical Newton gravitation law is found.
The gravitational constant in Newton’s law, G, is expressed by ![]() in which the parameter
in which the parameter![]() , equal to 2.34 ´ 104 m/(kg)4, can be seen as a universal constant that connects relativity with quantum mechanics.
, equal to 2.34 ´ 104 m/(kg)4, can be seen as a universal constant that connects relativity with quantum mechanics.
The surprising, and at the same time bizarre, conclusion of the analysis given is that, apparently, each single particle has interaction with all other particles. It means that in the universe an unimaginable number of pair-wise interactions exists with greatly varying intensity and extensions and which depend on the masses of the members of the pair. It is difficult to comprehend, but it follows unambiguously from the equations describing the behaviour of the pairs.
An important aspect to mention is the fact that the right hand side in Equation (12) should be invariant under Lorentz transformation. However, the rkl is not. Therefore the parameters ![]() should transform in the same way as rkl, but apparently it would make left and right hand side in equation 16 transform differently, which cannot be the case. We should however notice that the Planck’s constant, h, is invariant, but
should transform in the same way as rkl, but apparently it would make left and right hand side in equation 16 transform differently, which cannot be the case. We should however notice that the Planck’s constant, h, is invariant, but ![]() is not.
is not.
Make the following “thought experiment”. Consider a pair flying away from us at a speed v such that the separation vector of the members of the pair is aligned in the direction of v. Due to the fact that π transforms just like 1/rkl the result is that the interaction energy of the pair we measure becomes invariant. There is invariance throughout if the alignment is perpendicular to the speed. So the conclusion is that the interaction energy in the pair is invariant and independent of the alignment towards the observer, as it has to be.
Two remarks have to be made about the analysis proposed:
1) Equation (16) allows for both minus and plus signs for the E-values. It means that the force between particles can be negative and positive: repulsive and/or attractive. Apparently nature as we observe it has chosen for the low energy attractive variant. If the opposite would have been taken the universe could not exist.
2) The Equation (3) has singularities for rkl to zero. However, one might take the ![]() constant below a certain distance (
constant below a certain distance (![]() ) from the particle centre and solve the Equation (8) for just one single particle and see that, differing from the analysis for pairs, a first order solution emerges and mass (
) from the particle centre and solve the Equation (8) for just one single particle and see that, differing from the analysis for pairs, a first order solution emerges and mass (![]() ) is attributed to the particle, which to some extent is in analogy with superconductivity to explain the Meissner effect [1] [9] [10] .
) is attributed to the particle, which to some extent is in analogy with superconductivity to explain the Meissner effect [1] [9] [10] .
6. Conclusions
1) Using basic rules of quantum mechanics and relativity and preserving side conditions of invariance and co-variance where necessary, Newton’s law on gravity can be derived theoretically. It contains the main factors of mass dependence and distance between particles and bodies in the right way.
2) It has by no means relevance to dark matter or dark energy. But the result allows for both attractive and/or repulsive gravitational interaction. It can be speculated that at certain distance or strength of the interaction it may change sign.
Acknowledgements
The author thanks the Eindhoven University for giving the support to perform and publish this study.
Auke Veringa (averinga@versatel.nl) has been of great help to increase the accessibility of this paper also for non specialists in this field.
1The analysis is based on standard arguments of quantum theory and specific and general relativity theory. Specific reading on the separate subjects in monographs which are easily accessible to appreciate the foregoing analysis can be found in [3] [4] together.