A New Hybrid Order Approach to Morphological Color Image Processing Based on Reduced Order with Adaptive Absolute Reference ()
1. Introduction
With recent scientific advances made in the development of high resolution image sensors and in the increase of memory capacity, image processors have no technical problem to acquire multicomponent images of all types (spectral, temporal, etc.). They provide more detailed information of the properties of a scene, and allow more precise discrimination of objects.
Unfortunately, the processing methods of scalar images do not apply directly to multivariate-image [1] . This is not a new issue, since many authors have studied the case of color images which represent the most frequent case of multivariate images. Some works were based on the extension of the median filter to color images [2] and others on mathematical morphology extension to color images and more generally to the multimodal image [3] - [5] .
But this requires the definition of new orders for the extension of the scalar algorithms vector case. The main issue with this kind of extension is based on the definition of a suitable vector ordering, because there is no natural ordering for vectors particularly in the case of mathematical morphology that makes it complex for color images application. Owing to the vector like nature of the data, five approaches have retained our attention to order multivariate data [3] [4] , namely: i) the marginal order or M- order, ii) the conditional order or C-order, iii) the reduced order or R-order, iv) the partial order or P-order, and v) bit mixing order.
In marginal order, vector components are ordered separately. This approach produces new colors that are not from the colors of the original image, commonly called false colors. Also, it does not take into account the correlation between the components. In order to preserve the vectors output colors, conditional order was proposed.
In this approach, vectors are ordered components by components; unfortunately this order favors the first components. Moreover, the color metric in the sense of a metric is not guaranteed.
In reduced order, each vector is transformed into a scalar and vector data are sorted according to the order of the values obtained. Unfortunately it generates multiple extremums and requires the choice of a referent which is arbitrary.
As for the partial order, the vectors are grouped into subsets and are then ordered. This order is based on the geometric structure of the vectors. The disadvantage of this approach is that it does not propose an order within each partition.
Finally, the bit mixing order attempts to standardize the contribution of each modal component, but merges with the lexicographical order in its final principle.
In fact, during the last twenty years, the extension of mathematical morphology to color image and more generally to hyper spectral images was the subject of active researches, thus several approaches were proposed [4] [5] [7] . One such proposal was the color space (HVS) in lexicographical order by Louverdis in [8] . Recently Aptoula et al. proposed the α-lexicographical order, and on the basis of this proposed order, they built the multivariate morphological operators [9] [10] in order to improve the performance of multivariate morphological operators for color images filtering and segmentation. As for Angulo, he studied the quaternion properties and applied those properties to the color image decomposition. He then proposed a new lexicographical order based on quaternion decomposition. This approach gave better results [11] . Lei et al. have proposed a vector order based on the fuzzy and then built up morphological operators. The proposed operators have a high filtering performance of color images [12] . Various complex mathematical tools such as support vector machines [13] , the PCA [14] components, probabilistic estimation extremas [15] are used to develop the multivariate morphological operators and improve filtering and segmentation of color images.
A useful idea consists in the introduction of a reference color as well as a metric and then defines the order between two points relatively to their distances to the reference color [16] . This concept of reference has already been used to define a partial order on the unit circle [17] , and another way of seeing the reduced order with the notion of color reference is the use of vector projection. However, the reduced order is only aimed for a partial so as to avoid multiple extremas, that is to say two different points which have the same distance compared to the reference, a total order is then required to complete it. This question was highly studied by Angulo et al. [18] . In this approach, the total order used is the conditional order, therefore the first image components are preferred.
To have a uniform distribution of the spectral or multimodal components of the image, unlike the conditional order, we propose a hybrid vector order that combines the reduced order and bit mixing order proposed by J. Chanussot and P. Lambert [6] , and offer this method which provides uniform contribution components while maintaining proximity metric between colors.
The structure of this paper is organized as follows. Section 2 presents the general concepts: A new hybrid order and definitions for mathematical morphology, on which our approach is based. In Section 3, we focus on their application to color images processing. The performance of the morphological operator is illustrated with some examples. Then the conclusions close the paper in Section 4.
2. New Vector Order Based on Adaptive Absolute Reference Complemented by the Bit Mixing
2.1. Principle
Selecting an order ensuring the entire property ensures that all vectors are comparable. Thus, it is certain that no new values are introduced into the result. Solutions based on reduced orders have disadvantages, based on the release of the asymmetric constraint. In this case, it is possible to obtain several equivalent extrema. Various solutions have been offered in the literature, including the selection of one of the candidate values according to a function of the position of the pixel in the considered neighborhood or comparison of candidate values using a total order. But the order used is the conditional order, which is highly asymmetric.
When used with morphological operators in any color space, we note that most of the decisions on the order of the vectors in a structuring element are taken at the first level of the relation order [19] . This gives operators which are not homogeneous in their processing of the space. To overcome this problem, we offer to use this approach in the order by bit mixing instead of the conditional order; because it limits the dissymmetry between the components.
The approach is that, this time we offer to use absolute adaptive referents. It has the advantage of not choosing arbitrarily the reference colors and also it solves the problem of false color generated by the marginal order.
Let I be the matrix associated with a multicomponent digital image of N plans and V the matrix of order 3 × 3 of neighboring pixels of a spatial (i,j) of a coordinate pixel p. We note Max and Min conventional comparison operators that are the maximum and minimum, respectively.
And either define as:
Let 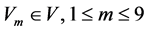 des N-uplets and define
des N-uplets and define 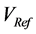 so as:
so as:
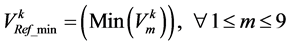 (1)
(1)
And
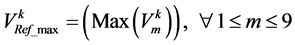 (2)
(2)
The dilated Vmax and the eroded Vmin of the neighborhood V of the pixel p are defined by the following expressions:
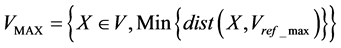 (3)
(3)
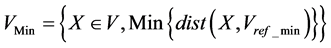 (4)
(4)
In the case of no unicity of Vmax and Vmin the solution vectors are ordered according to the vector order by bit mixing.
2.2. Bit Mixing Coding
Following the formalism introduced in [6] , the proposed technique; here is based on a transformation h that codes each pixel (vector) of the multicomponent image as a scalar. One may therefore order any group of vectors by placing their images h. The transformation h proposed here is based on the binary representation of each of the component of the vector C which one considers. If the N components are encoded on the same number p of bits we then have N × p bits which are mixed so as to construct a scalar N × p bit-coded by image. There are of course many ways to mix these bits, but in the absence of a priori knowledge about the relative share of information carried by each component the most symmetrical combination is chosen .Therefore we placed alternately the first bit of C(1) and the first bit of C(2) till and the C(N) bit and then moves to the second bit and so on until pth bit. Analytically, this can be expressed by the following formula:
 (5)
(5)
2.3. Algorithm
Let I be a multicomponent image of N components, V a neighborhood of order 3 × 3 around a pixel p of coordinates (i,j) and, L and M are respectively the number of rows and columns of the image.
For i = 1 to L do
For j = 1 to M do
1. Determination of the neighborhood W = V(p) around the pixel p(i,j)
2. Determination of the following parameters: 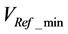 and
and 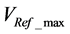
3. If several Vmax and Vmin:
・ In case of several Vmax
Calculation of the image of Vmax by the function h, then choose the tuple which has the largest Vmax obtained by h.
・ In case of several Vmin
Calculation of Vmin image by the function h, then choose the tuple that has the smallest Vmin obtained by h.
End for
End for
2.4. Performance of the Approach
To study the performance of this approach, we first studied the impact of different orders on a set of vectors of compact histogram [20] of synthetic and real images orderly default in lexicographical order. Moreover, we studied the influence of those orders on the detection of color contours through the implementation of morphological operators such as gradient and Laplacian as well as their edge detection quality through evaluation methods [21] in Table 1. Then we check the noise effect on images from impulse noise power levels to examine the robustness of our median filter and our vector order in face of noise.
We designed the following three color synthetic image Synt3a_Sie and used the Savoise image to illustrate the operation of the studied orders. The presented compact histograms contain colors and their numbers are sorted in lexicographical order.
3. Results and Interpretations
3.1. Tuples Ranking Analysis by Vector Orders
In Figure 1, the compact histogram by itself always present colors or tuples ordered
![]()
Table 1. Ascending ranking of different vector orders on Synt_3a image. Crefmin = (57, 50, 50) for the proposed order and Crefo = (68, 50, 50) for the reduced order. O1: Order Lexico, O2: Order by bit interlacing, O3: Reduced Order, O4: Proposed Order.
![]()
Figure 1. Synthetic Image Synt3a_Sie and its compact histogram lexicographical order.
according to the lexicographical order. We naturally note that the colors C1 and C3 are similar, but this order put C2 near C1 relatively to C3. In fact, we can say that this order does not favor the concept of the closest neighbor of real numbering the sense of a metric or the classical order of its own.
By applying the marginal order to all colors {C1, C2, C3}, we get Min {C1, C2, C3} = (57, 50, 50) and Max (C1, C2, C3) = (79, 200, 255). Through this example two disadvantages of the partial order are highlighted. First, the maximum does not belong to the whole definition of the image, hence it generally does not favor the classification of the colors of the image. Secondly this order produces only two colors instead of three. Therefore, in the general case where the image contains (N > 2) colors this order also produces two colors, one as minimum and the other as maximum.
In the case of reduced order, the reference color is chosen arbitrarily. If we consider color reference CrefO = (68, 50, 50).
We notice that the colors C1 and C2 are equal. Indeed, in such a way that, for a compact histogram of any given image we can always find a reference color CrefO so as two colors different or distant may be equal .Thus the choice of an optimal reference is mandatory. To solve the problem of multiple extremas, some authors have reclassified targeted tuples generally by choosing lexicographical order to obtain a total order.
Through the analysis of the tuples ranking based on vector orders, we can note that the choice of a single or absolute reference in the case of reduced order would help to avoid different scenario. Moreover, the lexicographical order is highly dissymmetric. This gives way to operators who are not homogeneous in their processing of space.
For theimageSynt3a, seeing the Table 1, the proposed order gives the desired natural result of ascending order of colors in the compact histogram. Here, the reduced order gives the same result, which would be a chance due to the choice of Crefo.
Table 2 presents the results of different vector order in ascending order. The color of the compact histogram Savoise image is illustrated in Figure 2. In this table we notice that the lexicographical orders and order by bit mixing could have a similarity but with significant difference in some tuples. It is the same for the reduced order and the proposed hybrid order.
An analysis of the results presented here and those obtained on other images, such as real images (House, Peppers, Lena, Mandrill, etc.) show that the choice of adaptive reference in our proposal depends on the content of the image and is well suited to
![]()
Table 2. Ascending ranking of different vector orders on Synt_3a image. Crefmin = (57, 50, 50) for the proposed order and Crefo = (68, 50, 50) for the reduced order. O1: Lexicographical Order, O2: Order by bit mixing, O3: Reduced Order, O4: Proposed Order.
![]()
Figure 2. Synthetic Savoise image and its lexicographical compact histogram order.
solve the problem of reduced order. And that the similarity between these two orders is due partly to the content (Crefmin and Crefmax) of the image and/or in the other hand, the arbitrary choice of Crefo which worths here (0, 0, 0).
However, the similarity between the lexicographical and order by bit mixing is due to the symmetry in base 2 of the level of each color compact histogram component.
In fact, our contribution includes firstly the determining of a minimum reference or absolute maximum, and then by successive eliminations, is classified in ascending order of the colors compact histogram. Here Crefmin = (57, 50, 50) and Crefmax = (79, 200, 255). In case of equality, the targeted colors are ranked by the order of bit interlacing which limits the asymmetry between the components.
3.2. Morphological Gradient and Laplacian
In image processing, the Gradient and the Laplacian are operators which allow bringing out the high frequency information in an image. Indeed, the latter carry out a contour detection function. In discrete functional mathematical morphology, they rely on two basic operators which are dilation and erosion. Those elements correspond to the maximum and minimum in the vicinity of a pixel of the image commonly known as structuring element vector. In this work, we made use of the symmetric Laplacian. The following formulas describe these operators:
Let I be a multicomponent image with n (n > 1) component and B a structuring element. We notice δB(I) the dilated form of I with respect to B and εB(I) the eroded form of I with respect to B. Let Max and Min respectively be the maximum and minimum of the elements of a set.
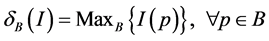 (6)
(6)
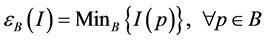 (7)
(7)
which lead us to the following expression of the Gradient (GradB) and Laplacian (LaplB), respectively noted:
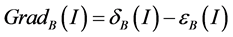 (8)
(8)
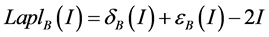 (9)
(9)
3.3. Analysis of Gradient and Laplacian Operators
The determination of Laplacian and gradient images is simple. In one word, one must know that the processing is carried in the image plan. First, for each pixel to be processed, a minimum reference and an absolute maximum adaptive reference are determined around a predefined neighborhood. Then the gradient and the Laplace are calculated through analytical expressions depending on the minimum and maximum previously determined.
Figure 3 shows a comparison of the gradient and Laplacian image with image House deriving from the reduced order, the order by bit mixing, the lexicographical order, the marginal order, and the proposed hybrid order. Contrast calculation or expert truths can allow us to quantify the differences between the orders but visually, gradient images show that our hybrid order is close to the reduced order and the marginal order but present the best results compared to the results of order by bit mixing and the lexicographical order on all of the processed images.
The Laplacian images show that the studied orders appear to produce similar results to ours, but are the best contrasted. However, it should be noted that our approach is designed to correct some shortcomings inherent to the studied orders. In fact, our order is a total order and therefore can build a complete lattice, the main ingredient for the definition of the main operators of the vector mathematical morphology. Our proposal allows comparing two tuples in contrast to the marginal order, also, it does not generate multiple extrema as opposed to the reduced order; and finally does not favor the first components unlike the conditional order, allowing him to have a uniform distribution of the spectral or multimodal components of the image.
However, a quantitative validation of our gradient and Laplacian operators through the proposed hybrid order is necessary. Unfortunately, there are no direct methods to assess results of these operators.
Therefore, a binary segmentation and thresholding has been necessary to us for contour segmentation of images; for this purpose, we used the thresholding method of Otsu
![]()
Figure 3. Gradient and Laplacian images for different orders of the House image.
[22] . At this stage, we used several methods to evaluate segmentation contours [21] to assess indirectly our gradient and Laplacian results also, in the literature the evaluation methods proposed are supervised like type that is to say, they require ground truth or expert segmentations.
In fact, the database Benchmark BSDS300 [23] with an image database and an expert contour segmentation has allowed us to evaluate our edge detection operators through various vector order. Figure 4 shows two (02) images of the benchmark based on their ground truths.
From a quantitative point of view, different contours segmentation assessment mea- sures were calculated to assess the relevance of our edge detection operators. This is the case of the Haussdoff distance, merit of the figure of Pratt and the extent of Vinet.
Table 3(a) and Table 3(b) present the results of the evaluation of the gradient and the Laplace studied through various orders. The Haussdoff measure generally provides constant values for the different vector order and does not discriminate their performance, we have not presented these results specifically. However, the figure of Pratt and Vinet measured allows discriminating their relevance. All the results from the different images of the base show that the proposed hybrid approach is effective in general than other levels, then comes the marginal then the reduced order as indicated in part in Table 3(a) and Table 3(b) below obtained from measurements of Pratt and Vinet. The lower the measure the better edge is the detection operator.
![]()
Figure 4. Images of the Benchmark base BSDS300 with their expert segmentations.
(a) ![]() (b)
(b) ![]()
Table 3. (a) Performance of gradient and Laplacian operators relating to the different vector orders (Measure of Pratt); (b) Performance of gradient and Laplacian operators relating to the different vector orders (Measure of Vinet).
3.4. Noise Robustness
To test the effectiveness of our proposal to noise, we added impulse noise to different images in order to study the robustness of the approach proposed and realized median filter. Here, we have illustrated the performance of our approach through an image base. For the presentation we chose two images a natural one corresponding to image House and the other a synthetic named Savoise. Different noise powers were added to the images described by the parameter p.
For each noise image we applied the median filter using: the reduced order, marginal order lexicographical order, order by bit mixing and our proposed hybrid order. Then we calculated the error rate generated by each order. The results are shown in Table 4 and Table 5.
We notice that the results depend on the image content. Indeed the error rate for all orders are high for the image House, see Table 3 while they are relatively low for Savoise image, see Table 4.
The median filter produces the same error rate for taking p values 0.001, 0.007 and 0.01 for the different studied orders. But for p = 0.03 and 0.05, our proposal is robust as lexicographical order, the reduced order and the order by bit mixing.
4. Conclusions and Perspectives
Mathematical morphological has been widely used to process binary and grayscale images and its techniques have been applied to noise reduction, image enhancement, and feature detection. To perform a morphological operation on vector-valued image, an ordering of vector field is required. The problem of ordering of multivariate data is not new since a possible classification of such ordering was discussed in [3] .
In this article, we have offered a contribution aiming to define an hybrid vector or-
![]()
Table 4. Comparison of median filters relating to different vector orders studied on image House.
![]()
Table 5. Comparison of median filters relating to different vector orders studied on image Savoise.
dering which combines both reduced order and the bit mixing order. In fact, this order is total, in such a way it appears as the key or fundamental element in the definition of the mathematical morphology.
Several of the above tests showed that our proposal was robust as lexicographical order, the reduced order and the order by bit mixing for noise suppression.
In future work, we intend to make a more detailed study of the correlation or the existing similarity between different orders and still propose a new more robust order, taking a best similarity into account. Besides, we would also take a look at the development of a new method for morphological segmentation vector-thresholding.