1. Introduction
Researchers in the field of nanotechnology are interested more and more in the study of properties of nanostructures based on IIB-VIA semiconductors because of their applications in the development of new optoelectronic devices. Among these semiconductors we include mono-chalcogenide Zinc ZnX (X = O, S, Se, Te). These compounds are technologically important and are used in many applications [1] such as optical memories of high density, the semiconductor laser devices, the transparent photodetectors conductors, visual displays, solar cells…
The current researches in electronics and optoelectronics have deduced that studies of structural and electronic properties of these devices have a significant interest in their development of new nanotechnologies.
Recently, there have been many empirical and theoretical calculations by the ab-in- itio method of structural and electronic properties for the ZnX compounds [2] - [5] . Tsuchiya et al. [3] calculated the energy band structure and the density of states for ZnS using the method of empirical pseudo-potential. Walter et al. [4] used the empirical pseudo-potential method to calculate the band structure of ZnSe and ZnTe. Huang Ching et al. [5] used the LCAO method (The Linear Combination of Atomic Orbitals) to calculate the band structure and the density of states for ZnX compounds. Karazhanov et al. [2] have used the functional theory of density to calculate the electronic structure of ZnX. In this context, we seek to optimize the structural and electronic properties of binary semiconductors based on ZnSe crystallizing in the Zinc Blende structure (B3). Our work is based on the theoretical calculations using the Full Potential Linearized Augmented Plane Waves method (FP-LAPW) developed in the calculation of ab-initio. This technique of modeling and simulation requires some approximation methods such as Local Density Approximation (LDA) and Generalized Gradient Approximation (GGA) of the Theory of Functional Density (DFT) to study the structural and electronic properties of the ZnX compounds.
2. Calculation Method
Our ab-initio calculations are carried out by a self-consistent cycle by solving the Kohn-Sham equation, using the FP-LAPW technical method of the Density Functional Theory (DFT) [6] , as transposed into WIEN2k code [7] .
The Approximations of Gradient Generalized (GGA) and Local Density (LDA) [8] were used to determine the exchange-correlation potential.
In the FP-LAPW technique the heart electrons, semi-heart and the valence electrons are included in the core-electron interaction calculations (poly-electronic system) to obtain more accurate results, the unit cell of the atomic lattice is modeled by spheres of muffin-tin radius RMT, associated with the bound electrons and the atomic nucleus. Valence electrons are associated with the interstitial space between these spheres and are described by the wave vector k. In these two different regions, a set of basic equations of the FP-LAPW method is used [7] .
In the Zinc Blende phase (B3), the muffin-tin radius RMT Zn atoms and Se are respectively 2.24 a.u and 2.13 a.u. Cutting the module reciprocal lattice vector Kmax = 9.5/Rmin, Rmin with the smallest RMT selected for the determination of the plane waves necessary for the expansion of the wave function in the interstitial region. The maximum value for the expansion of the wave functions inside the spheres was taken by default to Lmax = 10. The Gmax parameter was between the range Gmin = 8.92019 ≤ G ≤ Gmax = 12 which determines the Fourier development of precision, it is used to truncate the development plane wave potential and the charge density.
A mesh point 740 k (9 × 9 × 9) was taken in the first irreducible brillouin zone of the structure (B3) ZnSe. In our work we have neglected the spin-orbit coupling. The self-consistency is considered converged when the total energy of the system is stable with a convergence criterion of 0.0001 Ry and 0.001 e for charging and while imposing a separation with a cut-off energy (eCut) −6.0 Ry between core states and valence states.
3. Results and Discussions
3.1. Structural Properties
Our ab-initio calculations are carried out in conditions of zero pressure and temperature 0 K. The volume optimization was performed using the experimental value of the lattice constant of which is 5.667 (Å) for Zinc Blende phase ZnSe knowing that the space group F43 is 216-m. For atomic positions of Zn and Se respectively are in the positions (0, 0, 0) and (1/4, 1/4, 1/4) of the primitive unit cell. The variations of the total energy as a function of volume were used to determine the optimal lattice constant a, the compression module B and its derivative of pressure B'. With this technique, these parameters are calculated by adjusting the total energy in the Murnaghan equation of state [9] .
Equation (1): 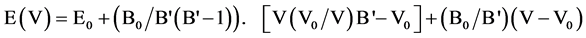
With 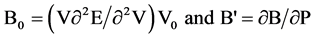
Figure 1 represents 3d modeling the primitive and unit cell of semiconductor ZnSe in the cubic phase Zinc-Blende realized by Xcrysden program.
![]() (a) (b)
(a) (b)
Figure 1. (a) Representation in perspective of the primitive cell of ZnSe in the ZB phase (B3); (b) Conventional representation of the unit cell of ZnSe in the ZB phase (B3).
Figure 2 represents the variations of the energy based on the volume of ZnSe in the Zinc Blende phase calculated with different approximations whose empirical parameters of the energy exchange-correlation are:
- Exc: Local Density Approximation (LDA),
- Exc: Perdew Burke Ernzerhof (PBE-GGA),
- Exc: The revised GGA Perdew-Burke-Ernzerhof (PBE-Sol),
- Exc: Wu and Cohen (WC-GGA).
The results derived from the curves in Figure 2 are prepared in Table 1 with experimental results and other results of theoretical calculation.
We see that our calculation gives results that are in good agreement with experimental values known in the literature.
We note that the GGA method parameterized by Wu and Cohen is here more efficient and gives significant improvements for calculating the lattice parameter “a” in the Zinc Blende structure of binary ZnSe.
3.2. Electronic Properties
3.2.1. Electronic Band Structure
The electronic properties of the ZnSe Zinc Blende phase are modeled using the optimal network parameter calculated previously. We treated orbital Zn [3p63d104s2] and Se [3d104s24p4] as valence states and for other orbitals are considered the states of the heart.
![]()
Table 1. Results derived from the curves in Figure 2 and other experimental and theoretical results calculated in the ZB phase (B3) ZnSe of the pressure 0 Pa and 0 K temperature.
aRéf [10] , bRéf [11] , cRéf [12] , dRéf [13] , eRéf [12] , fRéf [14] , gRéf [15] , hRéf [16] .
The 3d electrons Zinc represents a typical example, because the energy of the 3d orbitals are very close to the energy levels of electrons 4s and 4p. In addition the energy of the 3d orbitals are higher than those of the strips of the anion.
This is justified by their participation in the chemical bond. The treatment of electrons as valence states IIb-VIa semiconductor modify the properties of these systems near the maximum of the valence band [17] , [18] these effects imply a reduction in the energy gap and the cohesive energy and an increase in parameters of balance network.
Figure 3(a) and Figure 3(b) show the structures of the electronic band calculated along various lines of high symmetry by using the LDA and GGA-wc approximations.
It is clear that the band gap calculated by LDA and GGA-wc is underestimated compared with experimental results.
This underestimation of the band gap is mainly due to the fact that the simple form of these approximations does not take into account energy self-quasiparticle correctly [19] , this which does not make it flexible enough to accurately reproduce both the energy exchange-correlation and its derivative charge.
It is important to note that the formalism of the density functional theory is limited to the calculation of band structures and densities of states and we cannot compare directly these results with the experimental values [20] .
For that reason, we study the electronic properties of our material ZnSe in Zinc Blende phase by integrate the potential mBJ (modified Becke-Johnson potential) in our calculations, which we allowed to correct the energy gap [21] . To improve our band structure calculations and the density of states we use the mBJ-LDA and mBJ-GGAwc approximations by adopting the value optimal network parameter calculated by GGA-WC method with a GGAwc = 5.6551 (Å). Figures 4(a) and Figure 4(b) show the structure of electronic bands calculated by mBJ-LDA and mBJ-GGAwc respectively.
It is clearly seen that the energy of gap is corrected. The energy band structures of ZnSe component are qualitatively similar.
The results of important characteristics of band structures identified in Figure 3(a) and Figure 3(b), Figure 4(a) and Figure 4(b) are shown in Table 2 with other experimental and theoretical results.
All of the energies are in eV. NLPM: non-local pseudopotential; LCGO: linear combination of Gaussian orbitals; SE-TBM: semi empirical tight binding method.
![]()
Figure 3. Electronic band structures of ZnSe determined with LDA (a) and GGA-wc. (b) approximations.
![]()
Figure 4. Electronic band structures of ZnSe determined with mBJ-LDA (a) and mBJ- GGA-wc (b) approximations.
![]()
Table 2. Results deduced from curves in Figure 3(a), Figure 3(b), Figure 4(a) and Figure 4(b) with others experimental data or calculated by other techniques in the ZB phase (B3) of the ZnSe component.
aRef. [22] , bRef. [23] , cRef. [24] , dRef. [25] , eRef. [26] , fRef. [27] , gRef. [28] , hRef. [29] , iRef. [30] , jRef. [31] , kRef. [32] .
It is observed that in the region of the valence band, there is a substantial dispersion of bands in the branches ГX and ГL and there is also a small dispersion in the XK direction that demonstrates a weak interaction between layers. These bands along XK show of the localized electronic states [33] .
The bands of structures ZnSe are qualitatively similar and the minimum of the conduction band and the maximum of the valence band are located at the same point Γ. So our material belongs to the category of direct gap semiconductors.
Analysis of these band structures for binary component ZnSe gives a Span width of the valence band assessed between 13 eV and 13.6 eV calculated by the different approximations.
Is found that the gap values calculated by the mBJ-LDA and mBJ-GGAwc method are closer to the experimental results than those calculated with the LDA and GGA-wc approximations.
3.2.2. Density of State
In order to better understand the electronic properties of semiconductor ZnSe in Zinc Blende phase, we have studied qualitatively the total density of states (TDOS) ZnSe in the fundamental state and the partial density (PDOS) for the cation states (Zn) and the states of the anion (Se).
In our calculation, we used a mesh of 2000 k-point in the first brillouin zone. Figure 5
![]()
![]()
![]()
Figure 5. (a), (b) TDOS of ZnSe calculated by GGA-wc and mBJ-GGAwc respectively; (c), (d) PDOS of the cation states (Zn) calculated by GGA-wc and mBJ-GGAwc respectively; (e), (f) PDOS of the anion state (Se) calculated by GGA-wc and mBJ-GGAwc respectively.
illustrates the different contributions to the density of total and partial states of ZnSe, respectively calculated with the GGA-wc approximation and with the modified Becke- Johnson correction (mBJ-GGAwc).
Starting from the total densities one sees clearly that in the Zinc Blende structure (B3) ZnSe, the lower part of the valence band is dominated by chalcogenide states (Se). Although the upper part is occupied by the states of cation (Zn).
It emerges from the partial densities represented in graphs (5-c) and (5-d) that the strong peak in the valence band comes from the contributions of 3d-states Zn situated at approx −6 eV and we also note that the chalcogenide statements p and 4s dominate at the level close to the Fermi energy in the valence band. It appears that the contributions of states s and p of anion (Se) and the states s and p of the cation (Zn) predominate in the conduction band.
It appears that the contributions of states s and p of anion (Se) and the states s and p of the cation (Zn) predominate in the conduction band. It likewise identifies in the same band a not insignificant presence of d orbitals of the anion (Se).
According to our decomposition of the total density to of partial densities, we have shown that the main mechanism of the chemical bond is hybridization between states p of anions Se with 3d and 3p states of Zn cations at the top of the valence band.
One can conclude that the chemical bond of ZnSe semiconductor in the ZB phase (B3) has a covalent and ionic character simultaneously.
The results the density of states of ZnSe in Zinc Blende phase calculated with different approximations GGA-wc and mbj-GGAwc are illustrated on Figure 5.
3.2.3. Density of Electronic Charge
The fundamental reason for the study of the electronic charge density is to understand the nature of the chemical bond and their properties. Indeed, it explains the charge transfer between the atoms constituent of our material. Density contours of electronic charges from the valence band were calculated by GGA-WC approximation and they are plotted in the (1 1 1) plan and are shown in Figure 6.
Starting from the 3D representation of the distribution of electronic charges in the binary ZnSe Zinc Blende phase is clearly seen that there exists a charge distribution between atoms of zinc and the atoms of Selenide (Chalcogenide). The charge transfer difference between the constituent atoms is due to the difference in electronegativity between Zn/Se. Increasing the electronegativity difference between cations and anions results by a corresponding increase in the charge transfer, which is quite logical. It is clear that the chemical bond character is mixed (ionic and covalent).
The covalent chemical bonding is due to the charge sharing between the cation-Zn and anion-chalcogenide Se, while the binding is ionic in nature because there are no overlaps between contours. Also d-Zn states are the primary source of the charge around the cation sites whereas the charge around the anion sites is due to the contribution of the two states s and p. The hybridization between states p if anions with Zn cation of states in the valence band verify that our chemical bond is both covalent and ionic.
![]() (a)
(a)![]()
![]() (b)
(b)
Figure 6. Density of electronic charge. (a) Distribution of the ZnSe electronic charge in 2-D in the Zinc Blende phase (B3); (b) Distribution of the ZnSe electronic charge in 3-D in the Zinc Blende phase (B3).
4. Conclusions
Our modeling results of structural and electronic properties of ZnSe-based nanostructures in the Zinc Blende phase using the FP-LAPW method with approximations such as LDA, GGA, and mBJ are in good agreement with the theoretical results and experiments available.
We have also shown that the calculation of the lattice parameter “a” strongly depends on the choice of the functional exchange and correlation.
The LDA and GGA approximations are sufficient to optimization of the parameter structure, but they are insufficient for optimizing the band gap energy.
Recourse to mBJ approximation is necessary for the improvement of our calculation of the value of the gap.
The analysis of the profiles of densities of the electronic states and the density of the electronic charges shows that the structure presents some bonds which are both covalent and ionic.