Effects of Hydromagnetic and Thermophoresis of Unsteady Forced Convection Boundary Layer Flow over Flat Plates ()
1. Introduction
In recent years, the problems of forced convective boundary layer flow over flat plates with thermophoresis under the influence of a magnetic field have been attracted the attention of a number of researchers because of their possible applications in many branches of science and technology, such as its applications in transportation cooling of re-entry vehicles and rocket boosters, cross-hatching on ablative surfaces and film vaporization in combustion chambers. Forced convective boundary layer flows have a great interest from both theoretical and practical point of views because of its vast and significant applications in cosmic fluid dynamics, solar physics, geophysics, electronics, paper production, wire and fiver coating, composite processing and storage system of agricultural product etc.
A radiometric force by temperature gradient that enhances small micron sized particles moving toward a cold surface and away from the hot surface is termed as thermophoresis. The velocity caused by thermophoresis is called thermophoretic velocity. Thermophoresis plays a significant role of transporting particles from hot fluid region to the cold fluid region. This phenomenon has many engineering applications in removing small particles from gas streams, in determining exhaust gas particle trajectories from combustion devices, and in studying the particulate material deposition on turbine blades. Thermophoresis principle is utilized to manufacture graded index silicon dioxide and germanium dioxide in the fabrication of optical fiber used in the field of communications. Thermophoresis is also a key mechanism of study in semi-con- ductor technology especially in production of controlled high-quality wafer as well as in production of magnetohydrodynamic (MHD) energy. Thermophoretic deposition of radioactive particles is one of the major factors causing accidents in nuclear reactors. The magnitudes of the thermophoretic force and velocity are proportional to the temperature gradient and depend on many factors like thermal conductivity of aerosol particles and carrier gas. Duwairi and Damesh [1] investigated the effects of thermophoresis particle deposition on mixed convection from vertical surfaces embedded in saturated porous medium. Adrian Postelnicu [2] studied the thermophersis partical deposition in natural convection over inclined surfaces in porous media. Due to practical importance of thermophoresis phenomenon, Goren [3] analyzed thermophoresis in laminar flow over a horizontal flat plate. He found the deposition of particles on cold plate and particle free layer thickness in hot plate case. The deposition efficiency of small particles due to thermophoresis in a laminar tube flow was calculated by Walker et al. [4] . Rahman et al. [5] analyzed the local similarity solutions for unsteady two dimensional forced convective heat and mass transfer flow along a wedge with thermophoresis. Aldoss et al. [6] studied combined free and forced convection flow past a vertical plate embedded in a porous medium in the presence of a magnetic field. Ali et al. [7] studied a case of similarity solution for unsteady laminar boundary layer flow in curvilinear surface. Seth and Ansari [8] investigated unsteady hydromagnetic natural convection flow of a viscous, incompressible, electrically conducting and heat absorbing fluid past an impulsively moving vertical plate with ramped temperature embedded in a fluid saturated porous medium taking into account the effect of thermal diffusion. Nandkeolyar and Das [9] studied unsteady MHD free convection flow of a heat absorbing dusty fluid past a flat plate with ramped wall temperature. Kim [10] considered hydromagnetic natural convection flow past a vertical moving plate embedded in a porous medium. Ishak et al. [11] studied the steady laminar MHD boundary layer flow along a wedge immersed in an incompressible micropolar fluid in the presence of a variable magnetic field. Elbashbeshy et al. [12] studied the effect of magnetic field on boundary layer flow over an unsteady stretching surface in a micropolar fluid. Alam and Chapal [13] introduced a new similarity approach for an unsteady two dimensional forced convective flow of a micropolar fluid along a wedge. Jia et al. [14] studied the interaction between radiation and thermophoresis in forced convection laminar boundary layer flow. Chiou [15] analyzed the effect of thermophoresis on submicron particle deposition from a forced laminar boundary layer flow on to an isothermal moving plate through similarity solutions. Selim et al. [16] studied the effect of thermophoresis and surface mass transfer on mixed convection flow past a heated vertical flat permeable plate. Seth and Sarker [17] considered the hydro magnetic natural convection flow with induced magnetic field and nth order chemical reaction of a heat absorbing fluid past an impulsively moving vertical plate with ramped temperature. Parvin et al. [18] studied the effect of Prandtl number on forced convective flow and thermal field characteristics inside an open cavity with porous wavy isothermal wall using water-CuO nanofluid. Chamkha [19] studied unsteady hydromagnetic two dimensional convective laminar boundary layer flow with heat and mass transfer of a viscous, incompressible, electrically conducting and temperature dependent heat absorbing fluid along a semi-infinite vertical permeable moving plate in the presence of a uniform transverse magnetic field. Jhankal and Kumar [20] have analyzed the MHD boundary layer flow past a stretching plate with heat transfer. Bhattacharyya [21] discussed the mass transfer on a continuous flat plate moving in a parallel or reversely to a free stream in the presence of a chemical reaction. Kuiry and Bahadur [22] studied MHD flow of viscous fluid between two parallel porous plates with heat transfer in an inclined magnetic field. Khan et al. [23] have analyzed the effects of magnetic field on radiative flow of a nanofluid past a stretching sheet. The effects of thermophoresis and internal heat generation/absorption on MHD heat and mass transfer flow over an inclined radiate permeable surface were examined by Noor et al. [24] . Haddad et al. [25] experimentally investigated natural convection in nanofluid by considering the role of thermophoresis and Brownian motion in heat transfer enhancement.
The objective of the present paper is to obtain a local similarity solution of an unsteady two dimensional hydromagnetic forced convective boundary layer flow of a viscous incompressible fluid over flat plates with thermophoresis and be attempted to investigate the effects of several involved parameters on the velocity, temperature, concentration and other flow parameters like the skin-friction coefficient, local Nusselt number (wall heat transfer coefficient) and local Stanton number (wall deposition flux) across the boundary layer.
2. Mathematical Analysis and Governing Equations of the Problem
In this work, we considered the unsteady, laminar, hydromagnetic combined heat and mass transfer by forced convection flow along a flat plate. With x-axis measured along the plate, a uniform magnetic field 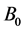 is applied in the y direction which is normal to the flow direction. A heat source is placed within the flow to allow for possible heat generation effects. The fluid is assumed to be Newtonian, electrically conducting and heat generating. The governing continuity, momentum, energy and diffusion equations can be written as:
is applied in the y direction which is normal to the flow direction. A heat source is placed within the flow to allow for possible heat generation effects. The fluid is assumed to be Newtonian, electrically conducting and heat generating. The governing continuity, momentum, energy and diffusion equations can be written as:
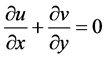 (1)
(1)
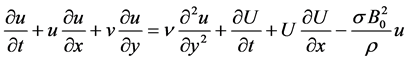 (2)
(2)
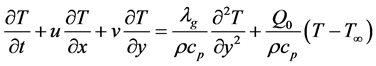 (3)
(3)
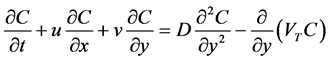 (4)
(4)
where 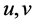 are the velocity components in the x and y directions respectively, v is the kinematic viscosity, g is the acceleration due to gravity,
are the velocity components in the x and y directions respectively, v is the kinematic viscosity, g is the acceleration due to gravity, 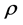 is the density of the fluid,
is the density of the fluid, 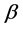 is the volumetric coefficient of thermal expansion.
is the volumetric coefficient of thermal expansion. 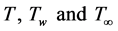 are the temperature of the fluid inside the thermal boundary layer, the plate temperature and the fluid temperature in the free stream, respectively, while
are the temperature of the fluid inside the thermal boundary layer, the plate temperature and the fluid temperature in the free stream, respectively, while 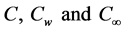 are the corresponding concentrations,
are the corresponding concentrations, 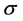 is the electrical conductivity,
is the electrical conductivity, 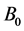 is the uniform magnetic field, U is the free stream velocity ,
is the uniform magnetic field, U is the free stream velocity ,  is the thermal conductivity of fluid,
is the thermal conductivity of fluid, 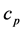 is the specific heat at constant pressure,
is the specific heat at constant pressure, 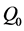 is the heat generation coefficient, D is the molecular diffusivity of the species concentration and
is the heat generation coefficient, D is the molecular diffusivity of the species concentration and 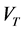 is the thermophoretic velocity. The
is the thermophoretic velocity. The
thermophoretic velocity 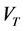 can be written as:
can be written as:
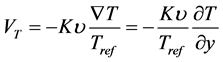 (5)
(5)
where k is the thermophoretic coefficient and Tref is the reference temperature.
The appropriate boundary conditions for the above model are as follows:
![]() (6)
(6)
and ![]() (7)
(7)
The continuity Equation (1) is satisfied by introducing the stream function ![]()
such that ![]() (8)
(8)
The momentum, energy and diffusion Equations (2)-(4) can be transformed to the corresponding ordinary differential equations by introducing the following similarity transformations:
![]() (9)
(9)
The momentum, energy and diffusion Equations (2)-(4) after some simplifications, reduce to the following forms:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
where, Pr (Prandtl number) = ![]() (13)
(13)
M (Modified Local Magnetic field Parameter) = ![]() (14)
(14)
Q (Modified local heat generation Parameter) = ![]() (15)
(15)
Sc (Schmidt number) = ![]() (16)
(16)
Ta (Thermophoretic Parameter) = ![]() (17)
(17)
The corresponding boundary conditions are:
![]() (18)
(18)
and ![]() (19)
(19)
where the prime ( ![]() ) denotes differentiation with respect to
) denotes differentiation with respect to![]() .
.
The Prandtl number (Pr) or Prandtl group is a dimensionless number and is defined as the ratio of momentum diffusivity to thermal diffusivity. The Prandtl number contains no such length scale in its definition and is dependent only on the fluid and the fluid state. As such, the Prandtl number is often found in property tables alongside other properties such as viscosity and thermal conductivity. For most gases over a wide range of temperature and pressure, Pr is approximately constant. Therefore, it can be used to determine the thermal conductivity of gases at high temperatures, where it is difficult to measure experimentally due to the formation of convection currents. Small values of the Prandtl number, ![]() , means the thermal diffusivity dominates. Whereas with large values,
, means the thermal diffusivity dominates. Whereas with large values, ![]() , the momentum diffusivity dominates the behavior. In heat transfer problems, the Prandtl number controls the relative thickness of the momentum and thermal boundary layers. When Pr is small, it means that the heat diffuses quickly compared to the velocity (momentum). This means that for liquid metals the thickness of the thermal boundary layer is much bigger than the velocity boundary layer. The mass transfer analog of the Prandtl number is the Schmidt number.
, the momentum diffusivity dominates the behavior. In heat transfer problems, the Prandtl number controls the relative thickness of the momentum and thermal boundary layers. When Pr is small, it means that the heat diffuses quickly compared to the velocity (momentum). This means that for liquid metals the thickness of the thermal boundary layer is much bigger than the velocity boundary layer. The mass transfer analog of the Prandtl number is the Schmidt number.
Schmidt number (Sc) is a dimensionless number with important applications to transport phenomena and is defined as the ratio of momentum diffusivity (viscosity) and mass diffusivity and is used to characterize fluid flows in which there are simultaneous momentum and mass diffusion convection processes. It physically relates the relative thickness of the hydrodynamic layer and mass-transfer boundary layer.
Thermophoretic parameter is a phenomenon observed in mixtures of mobile par- ticles where the different particle types exhibit different responses to the force of a temperature gradient. Thermophoretic force has been used in commercial precipitators for applications similar to electrostatic precipitators. It is exploited in the manu-fac- turing of optical fiber in vacuum deposition processes. It can be important as a transport mechanism in fouling.
Magnetic field Parameter is a dimensionless number used in magneto fluid dynamics, equal to the product of the square of the magnetic permeability, the square of the magnetic field strength, the electrical conductivity and a characteristic length, divided by the product of the mass density and the fluid velocity. Magnetic fields can be produced by moving electric charges and the intrinsic magnetic moments of elementary particles associated with a fundamental quantum property. Magnetic field lines would start or end on magnetic monopoles, so if they exist, they would give exceptions to the rule that magnetic field lines neither start nor end.
A heat generation site is a structure where heat is generated for distribution to other structures and its parameter is known as heat generation parameter. The power consumption and the heat generation in metal cutting processes are dependent on a combination of the physical and chemical properties of the work piece material and cutting tool material, cutting conditions and the cutting tool geometry.
Important Physical Parameters
The skin-friction coefficient, local Nusselt number (wall heat transfer coefficient), and local Stanton number (wall deposition flux):
The parameters of engineering interest for the present problem are the skin-friction coefficient, local Nusselt number and the local Stanton number which indicate physically wall shear stress, rate of heat transfer and wall deposition flux respectively. These can be obtained from the following expressions:
A dimensionless skin-friction coefficient expressing the proportionality between the frictional force per unit area, or the shearing stress exerted by the wind at the earth's surface, and the square of the surface wind speed. Skin friction coefficient is a component of parasitic drag that occurs differently depending on the type of flow over the lifting body (laminar or turbulent). Just like any other form of drag, the coefficient of skin friction drag is calculated with various equations and measurements depending on the flow and then added to coefficients of other forms of drag to calculate total drag.
The skin-friction coefficient is given by
![]() (20)
(20)
In heat transfer at a boundary (surface) within a fluid, the local Nusselt number is the ratio of convective to conductive heat transfer across (normal division by its area then takes care of the local factor and the normalization). The local Nusselt number analog has on occasion been used to actually.
The local Nusselt number may be written as
![]() (21)
(21)
The local Stanton number is a dimensionless number that measures the ratio of heat transferred into a fluid to the thermal capacity of fluid. This number arises in the consideration of the geometric similarity of the momentum boundary layer and the thermal boundary layer, where it can be used to express a relationship between the shear force at the wall (due to viscous drag) and the total heat transfer at the wall (due to thermal diffusivity).
The Stanton number can be written as
![]() (22)
(22)
where, ![]() is the wall shear stress on the surface,
is the wall shear stress on the surface, ![]() be the rate of heat transfer and
be the rate of heat transfer and ![]() be the rate of transfer of species concentration.
be the rate of transfer of species concentration.
3. Numerical Solution
The set of ordinary differential Equations (10) to (12) with boundary conditions (18) and (19) are nonlinear and coupled. A standard initial value solver i.e., the shooting method is used to solve these equations numerically. For this purpose we applied the Nacthsheim-Swigert iteration technique (Nachtsheim and Swigert, 1965) [26] . In the process of iteration the velocity, temperature and concentration profile, the skin-fric- tion coefficient, ![]() , local Nusselt number (wall heat transfer coefficient),
, local Nusselt number (wall heat transfer coefficient), ![]() and local Stanton number (wall deposition flux),
and local Stanton number (wall deposition flux), ![]() are evaluated. The numerical results obtained for several selected values of the established parameters are displayed in graphs and tables below. These graphs and tables show that velocity, temperature, concentration, wall heat transfer coefficient, wall deposition flux and the skin-friction coefficient are affected significantly with the variations of the considered controlling parameters.
are evaluated. The numerical results obtained for several selected values of the established parameters are displayed in graphs and tables below. These graphs and tables show that velocity, temperature, concentration, wall heat transfer coefficient, wall deposition flux and the skin-friction coefficient are affected significantly with the variations of the considered controlling parameters.
4. Results and Discussion
In order to investigate the physical representation of the problem, the numerical values of velocity field (![]() ), temperature field (
), temperature field (![]() ) and concentration (
) and concentration (![]() ) have been computed for resultant for various physical parameters like local heat generation parameter, Schmidt parameter, local magnetic field parameter and thermophoretic parameter. The parameters are chosen arbitrarily where Pr = 0.71 corresponds physically to air at 20˚C, Pr = 1.10 corresponds to electrolyte solution such as salt water and Pr = 7.0 corresponds to water, and Sc = 0.30 for helium and Sc = 0.60 water vapor at approximate 25˚C and 1 atmosphere. In order to get clear insight into the physics of the problem, a representative set of numerical results are shown graphically in Figures 1-15.
) have been computed for resultant for various physical parameters like local heat generation parameter, Schmidt parameter, local magnetic field parameter and thermophoretic parameter. The parameters are chosen arbitrarily where Pr = 0.71 corresponds physically to air at 20˚C, Pr = 1.10 corresponds to electrolyte solution such as salt water and Pr = 7.0 corresponds to water, and Sc = 0.30 for helium and Sc = 0.60 water vapor at approximate 25˚C and 1 atmosphere. In order to get clear insight into the physics of the problem, a representative set of numerical results are shown graphically in Figures 1-15.
4.1. Velocity Profiles
The dimensionless velocity profiles for the influence of various physical parameters are
![]()
Figure 1. Effect of dimensionless velocity profiles across the boundary layer for different values of M and for Pr = 0.71, Q = 2.50, Sc = 0.60, Ta = 0.50.
![]()
Figure 2. Effect of dimensionless velocity profiles across the boundary layer for different values of Pr and for M = 1.50, Q = 2.50, Sc = 0.60, Ta = 0.50.
presented in Figures 1-15.
Figure 1 presents typical profiles for the velocity for various values of the local magnetic field parameter, M. The presence of a magnetic field normal to the flow in an electrically conducting fluid introduces a Lorentz force which acts against the flow. This
![]()
Figure 3. Effect of dimensionless velocity profiles across the boundary layer for different values of Q and for M = 1.50, Pr = 0.71, Sc = 0.60, Ta = 0.50.
![]()
Figure 4. Effect of dimensionless velocity profiles across the boundary layer for different values of Sc and for M = 1.50, Pr = 0.71, Q = 2.50, Ta = 0.50.
resistive force tends to slow down the flow and hence the fluid velocity decreases with the increase of the local magnetic field parameter as observed in Figure 1. Higher the Lorentz force lesser is the velocity. This is true for steady and unsteady cases. This result qualitatively agrees with the expectations, since the magnetic field exerts a retarding
![]()
Figure 5. Effect of dimensionless velocity profiles across the boundary layer for different values of Ta and for M = 1.50, Pr = 0.71, Q = 2.50, Sc = 0.60.
![]()
Figure 6. Effect of dimensionless temperature profiles across the boundary layer for different values of M and for Pr = 0.71, Q = 2.50, Sc = 0.60, Ta = 0.50.
force on the forced convection flow.
Due to forced convection flow, the Prandtl number Pr affects the velocity distribution. Figure 2 represents the dimensionless velocity profiles for several values of the
![]()
Figure 7. Effect of dimensionless temperature profiles across the boundary layer for different values of Pr and for M = 1.50, Q = 2.50, Sc = 0.60, Ta = 0.50.
![]()
Figure 8. Effect of dimensionless temperature profiles across the boundary layer for different values of Q and for M = 1.50, Pr = 0.71, Sc = 0.60, Ta = 0.50.
Prandtl number Pr, the velocity along the plate decreases with increase in Pr. It is evident from the decrease in the velocity profiles along x-direction and y-direction respectively as Pr increases that, the fluid’s velocity components decrease at every point above
![]()
Figure 9. Effect of dimensionless temperature profiles across the boundary layer for different values of Sc and for M = 1.50, Pr = 0.71, Q = 2.50, Ta = 0.50.
![]()
Figure 10. Effect of dimensionless temperature profiles across the boundary layer for different values of Ta and for M = 1.50, Pr = 0.71, Q = 2.50, Sc = 0.60.
the surface.
Figure 3 displays the effects of the heat generation parameter Q on the velocity component. This is represented in the increases the fluid velocity as the heat generation parameter Q increases, as seen from Figure 3. This is expected since heat generation (Q >
![]()
Figure 11. Effect of dimensionless concentration profiles across the boundary layer for different values of M and for Pr = 0.71, Q = 2.50, Sc = 0.60, Ta = 0.50.
![]()
Figure 12. Effect of dimensionless concentration profiles across the boundary layer for different values of Pr and for M = 1.5, Q = 2.50, Sc = 0.60, Ta = 0.50.
0) causes the thermal boundary layer to become thicker and the fluid become warmer.
The influences of the Schmidt number, Sc on the velocity profiles are plotted in Figure 4. The Schmidt number embodies the ratio of the momentum to the mass diffusivity.
![]()
Figure 13. Effect of dimensionless concentration profiles across the boundary layer for different values of Q and for M = 1.5, Pr = 0.71, Sc = 0.60, Ta = 0.50.
![]()
Figure 14. Effect of dimensionless concentration profiles across the boundary layer for different values of Sc and for M = 1.5, Pr = 0.71, Q = 2.50, Ta = 0.50.
The Schmidt number therefore quantifies the relative effectiveness of momentum and mass transport by diffusion in the hydrodynamic (velocity). As the Schmidt number
![]()
Figure 15. Effect of dimensionless concentration profiles across the boundary layer for different values of Ta and for M = 1.5, Pr = 0.71, Q = 2.50, Sc = 0.60.
increases the velocity increases.
Figure 5 exhibits the behavior of dimensionless velocity profiles for some the values of the thermophoretic parameter Ta. From this figure it is clear that the fluid velocity increases rapidly with the increase of the thermophoretic parameter Ta.
4.2. Temperature Profiles
The dimensionless temperature profiles are presented in Figures 6-10.
For different values of the magnetic field parameter M on the temperature profiles are plotted in Figure 6. It is observed that the temperature profile slightly decrease with the increase of magnetic field parameter. Therefore, an applied magnetic field can be used to control the flow, rotation of micro-constituents and heat transfer characteristics.
Figure 7 illustrates the temperature profiles for different values of the Prandtl number Pr.
Prandtl number defines the relative effectiveness of the momentum transport by diffusion in the hydrodynamic boundary layer to the energy transported by thermal diffusion in the thermal boundary layer. According to the definition of Prandtl number high Pr fluids possess lower thermal conductivities which reduce the conduction heat transfer and increases temperature variations at the wall. The Prandtl number defines the ratio of momentum diffusivity to thermal diffusivity. This figure reveals that an increase in Prandtl number Pr results in a decrease in the temperature distribution, because, thermal boundary layer thickness decreases with an increase in Prandtl number, Pr.
From Figure 8, we observe that when the value of the heat generation parameter, Q increases, the temperature distribution also increases significantly which implies that owing to the presence of a heat source, the thermal state of the fluid increases causing the thermal boundary layer to increase.
The influence of the Schmidt number on the temperature is presented in Figure 9. From this fig. we see that the temperature monotonically decreases with an increase of Schmidt number, Sc.
The dimensionless temperature profiles along x-direction for different values of Ta are presented in the Figure 10 and also showing the effects of the thermophoretic parameter, Ta. It is observed that the temperature profiles decrease with the increase of the thermophoretic parameter, Ta.
4.3. Concentration Profiles
In order to gain physical insight of the problem, the numerical results for the dimensionless concentration profiles have been presented graphically in Figures 11-15.
The effect of the local magnetic field parameter (M) on concentration fields have shown in Figure 11. In Figure 11, the effect of an applied magnetic field is found to decrease the concentration profiles, and hence increase the concentration boundary layer with the increasing of magnetic field parameter (M).
From Figure 12, we can ascertain that the isotherms are almost linear and distributed inside the cavity for Pr = 0.71, which is due to the combined effect of conduction and forced convection. From this Figure 12, we observe that the temperature profiles increase swiftly with the increase of the Prandtl number (Pr).
In Figure 13, we have plotted the variation of the dimensionless concentration distribution for different values of Q and also showing the effects of the local heat generation parameter Q. It is seen from Figure 13 that when the heat is generated, the buoyancy force increase, which induces the flow rate to increase giving, rises to the increase in the concentration profiles. On the other hand, we see that the concentration profiles increase rapidly while the concentration boundary layer decreases as the heat generation parameter Q increases.
Figure 14 displays the variation of dimensionless concentration profiles for several value of Schmidt number, Sc. The Schmidt number embodies the ratio of the momentum to the mass diffusivity. The Schmidt number therefore quantifies the relative effectiveness of momentum and mass transport by diffusion in the concentration (species) boundary layers. As the Schmidt number increases the concentration also increases. This causes the concentration buoyancy effects to increase yielding a reduction in the fluid velocity.
The effect of the thermophoretic parameter (Ta) on concentration field is presented in the Figure 15. From Figure 15, it is noticed that the effect of increasing the thermophoretic parameter (Ta) increasing slightly the wall slope of the concentration profiles.
The skin-friction coefficient, ![]() , local Nusselt number (wall heat transfer coefficient),
, local Nusselt number (wall heat transfer coefficient), ![]() and local Stanton number (wall deposition flux),
and local Stanton number (wall deposition flux), ![]() are important physical parameters .These tables are given below.
are important physical parameters .These tables are given below.
The numerical results are illustrated in Tables 1-5 for the effect of various parameters on the Skin-friction coefficient, local Nusselt number, and local Stanton number. From Table 1, it is clear that the Skin-friction coefficient and the local Nusselt number increases while the local Nusselt number decreases with the increases of the local Magnetic field parameter (M). From Table 2 and Table 5, it is clear that the Skin-friction
coefficient and the local Nusselt number decrease while the local Nusselt number increases with the increase of the Prandtl number (Pr) and the Thermophoretic parameter (Ta) respectively. For the the increases of local heat generation parameter (Q), the Skin-friction coefficient and the local Stanton number decrease while the local Nusselt number inccreases in Table 3. In Table 4 revels that the Skin-friction coefficient and the local Stanton number increase while the local Nusselt number decrease with the increase of Schmidt number (Sc).
In the presence of a magnetic field, the fluid velocity is found to be decreased, associated with a reduction in the velocity gradient at the wall, and thus the local skin-fric- tion coefficient decreases. Also, the applied magnetic field tends to decrease the wall temperature gradient and concentration gradient, which yield a decrease the local Nusselt number and the local Stanton number. The local skin friction coefficient as well as rate of heat transfer in the micropolar fluid is lower compared to that of the Newtonian fluid. The above table is highly significant influences of on skin friction, the rate of heat transfer and wall deposition flux have been found which can be physically realizable.
5. Conclusions
In this paper, we have discussed the effects of thermophoresis on an unsteady two dimensional forced convective heat and mass transfer boundary layer flow over flat plates. The results are analyzed for various physical parameters such as local magnetic field parameter, Prandtl number, Schmidt number, local heat generation parameter, magnetic parameter, thermophoretic parameter, heat and mass transfer characteristics. The numerical results have been presented in the form of graphs and tables. The particular conclusions drawn from this study can be listed as follows:
・ Thermophoretic particle deposition velocity decreases with the increasing values of the thermophoretic coefficient and concentration ratio where as it increases with the increasing values of the thermophoresis parameter.
・ The plate couple stress increases with the increase values of the magnetic field parameter.
・ Magnetic field significantly controls the flow, rotation of micro-constituents and heat transfer characteristics of a micropolar fluid.
・ Magnetic field retards the motion of the fluid.
・ Thermophoresis is an important mechanism of micro-particles transport due to a temperature gradient in the surrounding medium and has found numerous applications, especially in the field of aerosol technology and industrial air pollution.
・ The Prandtl number as well as the Schmidt number varies significantly within the boundary layer when the thermal conductivity is temperature dependent.
・ In forced convection regime, the surface mass flux increases with the increase of the thermophoretic parameter.
・ The local skin friction coefficient, Nusselt number and Sherwood number are higher for the fluids of constant electric conductivity than those of the variable electric conductivity.
・ The velocity profiles increase whereas temperature profiles decrease with an increase of the forced convection current.
・ Concentration within the boundary-layer decreases with the increasing values of the thermophoretic parameter whereas it increases as increases the thermophoretic coefficient as well as the concentration ratio.