Numerical Investigation of a Mixed Convection Flow in a Lid-Driven Cavity ()
Received 12 May 2016; accepted 16 September 2016; published 19 September 2016

1. Introduction
One of the major problems in the thermos-fluids is the free and forced convection flow and heat transfer in different aspect of cavity. The lid-driven cavity flow is the motion of a fluid inside a rectangular cavity created by a constant translational velocity of one side while the other sides remain at rest. Fluid and heat flow behaviors inside lid driven cavities have been the subject of extensive computational and experimental studies over the past years. It has many applications in engineering, material processing, dynamics of lakes, metal casting and galvanizing.
The influence of a lid movement on the fluid flow and thermal structures in a lid-driven cavity was conducted by [1] . They concluded that the maximum local heat transfer rate occurs at the starting area of the sliding lid and decreases along the sliding lid. Mixed convection and conduction heat transfer in open cavities investigated numerically by [2] . They found that heat transfer across the cavity is enhanced when the cavity aspect ratio is increased. A combined forced and natural convection in a lid-driven cavity is investigated experimentally by [3] . The case of transient laminar mixed convention flow and heat transfer of an electrically conducting and heat generating in a lid driven cavity was investigated by [4] . He concluded that the existence of the internal heat generation decreases the average Nusselt number significantly. The unsteady free and forced convection in partially divided cavity were investigated by [5] . They found that the time to reach the steady state depends on the structure of divider.
The cubic interpolated pseudo particle method and verified their results with the shear driven flow in square cavities were considered by [6] . Li et al. [7] applied the new version of multiple relaxation time lattices Boltzmann method to investigate the fluid flow in deep cavity. Manca et al. [8] showed a numerical analysis of laminar mixed convection in an open cavity with a heated wall bounded by a horizontally insulated plate. Their results were reported for Reynolds numbers in the range of 100 to 1000 and aspect ratio from 0.1 to 1.5. They presented that the maximum decrease in temperature was occurred at higher Reynolds number. They found that the effect of the aspect ratio was played a significant role on streamlines and isotherm patterns for different heating configurations. Their investigations also indicate that opposing forced flow configuration has the highest thermal performance, in terms of both maximum temperature and average Nusselt number.
Gau and Sharif [9] investigated the mixed convection in rectangular cavities at various aspect ratios with moving isothermal side walls and constant wall flux heat source on the bottom wall. Numerical simulation of unsteady mixed convection in a driven cavity using an externally excited sliding lid is conducted by Khanafer et al. [10] . They observed that, Re and Gr would either enhance or retard the energy transport process and drag force behavior depending on the conduct of the velocity cycle. Recently, nanofluids, which are considered very promising in heat transfer enhancement, were used in several studies. Khanafer et al. [11] investigated the problem of buoyancy-driven heat transfer enhancement of nanofluids in a two-dimensional enclosure. Jang and Choi [12] investigated free convection in a rectangular cavity (Benard convection) with nanofluids. Jou and Tzeng [13] present a numerical study of the heat transfer performance of nanofluids inside two dimensional rectangular cavity.
Wang et al. [14] studied free convection heat transfer in horizontal and vertical rectangular cavities filled with nanofluids. Santra et al. [15] investigated heat transfer characteristics of copper water nanofluid in a differentially heated square cavity with different viscosity models.
Many researchers, investigate the mixed convection heat transfer characteristics of a square cavity over the years, however, there seems to be lack studies relates the numerical investigation covered the effect of aspect ratio. Therefore, the main objective of this study is to study the effect of aspect ratio (0.5 ≤ AR ≤ 1.5) on fluid and heat transfer characteristic for laminar, steady and mixed convection using commercial finite volume package FLUENT. Also, the present study focuses on flow visualizations on moderate Reynolds number range varying the aspect ratio of driven cavity.
2. Theoretical Formulation
The fluid flow and heat transfer in open lid driven cavity can be simulated by a set of mass, momentum and energy conservation equations. The flow is assumed to be two-dimensional, laminar, incompressible, Newtonian and neglecting the viscous effect. The dimensionless governing non-linear partial differential equations can be written as follows:
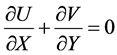 (1)
(1)
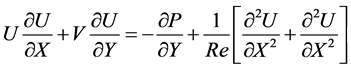 (2)
(2)
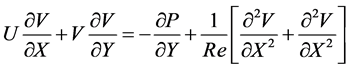 (3)
(3)
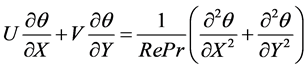 (4)
(4)
The dimensional variables are as follows:
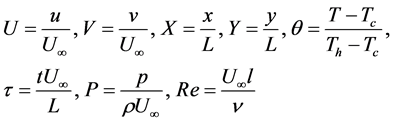 (5)
(5)
The L is the reference length dimension (width of the cavity along lower lid), while U∞ is the reference velocity dimension. The fluid property ν, refers to the kinematic viscosity. The Reynold’s number, Re, is the ratio of inertial to viscous forces, which influences the fluid flow features within the cavity. No-slip velocity boundary condition (u = v = 0) is applied on all the walls, except the top lid. On the top lid (U = 1 and V = 0) is applied. The bottom boundary of the domain is modeled as wall .The boundary conditions which describing the current simulated computational domain as well as the surface boundary layer is depicted in Figure 1.
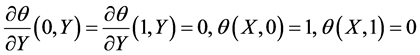 (6)
(6)
A finite volume method is employed using commercial software FLUENT 6.2 to solve the governing equations together with the specified boundary conditions. The velocities and pressure are coupled by the SIMPLE algorithm. More cells are constructed near the surface of the cavity to compensate the high velocity gradient in the boundary layer region of the viscous flow. A commercial software GAMBIT is used for grid generation. A second order upwind scheme is used for the convection. Here in this study, following [10] , we define the Nusselt number, 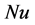 as follows:
as follows:
 (7)
(7)
 is the fluid thermal conductivity, Y is appropriate cavity length and
is the fluid thermal conductivity, Y is appropriate cavity length and 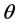 is non dimnial temperature. The grid independence is achieved by comparing the results of the different grid cell size. It was found that 65,000 cells are satisfactory, and any increase beyond this size would lead to an insignificant change in the resulting solution.
is non dimnial temperature. The grid independence is achieved by comparing the results of the different grid cell size. It was found that 65,000 cells are satisfactory, and any increase beyond this size would lead to an insignificant change in the resulting solution.
![]()
Figure 1. Schematic of the square lid-driven cavity.
3. Results and Discussion
Simulation results for laminar mixed convection in square cavity (AR = 1) are compared to experimental data to verify the validity of the CFD simulation solution. Then, the code is employed to investigate the mixed convection fluid flow and heat transfer inside the different aspect ratio of cavity. Figure 2 and Figure 3 show the U and V-velocity profiles at the vertical and horizontal mid-plane of the square cavity for (AR = 1). As can be seen there is an excellent agreement in the velocity profile between CFD simulations in this study and the experimental measured by [16] . It has been noticed that the heating of the surface of the cavity has no effect on the velocity profile.
Figure 4 shows the influence of the aspect ratio on the local Nusselt number for Re = 100. It is worth indicating that all the simulation results of local Nusselt number and temperature profile presented in this work correspond to the cold lid. It is noticeable, that the local Nusselt number decreases as x increase and increases as the
![]()
Figure 2. Computed of U-velocity profiles along a vertical line passing through the geometric centre of the cavity (at X = 0.5) at various aspect ratios, Re = 1000.
![]()
Figure 3. Computed of V-velocity profiles along a horizontal line passing through the geometric centre of the cavity (at Y = 0.5) at various aspect ratios, Re = 1000.
aspect ratio decreases for Re = 100. Decreasing the aspect ratio means that the cold lid would be close to the hot wall and sense the heat significantly. Therefore, the heat transfer enhanced near the cold lid.
Figure 5 shows the influence of the aspect ratio on the profile temperature for Re = 100 to the right wall. It is also noticeable, the profile temperature decreases as y increase and increases as the aspect ratio increases for Re = 100. For the same reason, increasing the aspect ratio means that the right wall would be close to the hot wall and sense the heat significantly. Therefore, the heat transfer enhanced near the right wall.
Figure 6 shows the influence of the aspect ratio on the profile temperature for Re = 100 to the left wall. It is also noticeable, the profile temperature decreases as y increase and increases as the aspect ratio increases for Re = 100. For the same reason, increasing the aspect ratio means that the right wall would be close to the hot wall and sense the heat significantly. Therefore, the heat transfer enhanced near the right wall.
The contours of static temperature that has the same temperature difference and various aspect ratio are shown in Figure 7. The mixed convection cases show different pattern. In order to visualize the overall thermal
![]()
Figure 4. Distribution of local Nusselt number at hot lid for various aspect ratios, Re = 100.
![]()
Figure 5. Typical profile of temperature θ distribution at hot lid for various aspect ratios, Re = 100.
patterns, the isotherm contours plots from the computational data for different aspect ratio are at Reynolds number = 100 is shown in Figure 8. For smaller aspect ratio the centre of the primary eddy moves right with
![]()
Figure 6. Typical profile of temperature θ distribution at left wall for various aspect ratios, Re = 100.
![]()
Figure 7. Typical profile of temperature θ distribution at mid of cavity for various aspect ratios, Re = 100.
![]()
Figure 8. Contours of static temperature in (K) inside cavity for various aspect ratios, Re = 100.
respect to right wall cavity. Further, an energy rate increases due to circulation movements of fluid molecules which enhance the thermal dispersion especially for smaller cavity aspect ratio.