Electromagnetic Modulation of Dipole Antenna inside an Infinite Rectangular Waveguide Using MoM-GEC ()
1. Introduction
Various types of electromagnetic source were used to model an antenna for mobile phone applications. A dipole antenna is the simplest and most widely used. The dipole antenna was modeled as perfect conductor with feeding gap at center between two arms. We consider a thin dipole antenna of “L” length being fed at its center.
A new formulation based on the integral-equation formulation in the frequency domain is used to study the behavior of a dipole antenna with finite length. The MoM method, designed and carefully optimized, can be a highly efficient and reliable tool for the analysis and design of many complex EM structures.
To validate the dipole antennas is designed using Hallen and Pocklington’s integral equations approximations [1] . Numerical techniques in solving electromagnetic problems are the most common methods, which are used with the budding inventions of high-speed computers and powerful software’s. Among these numerical techniques, Method of Moments (MOM) is a powerful numerical technique to solve integral equations and this technique will be applied on Hallen and Pocklington’s integral equations for a dipole antenna [2] .
The aim of the developed method is to investigate the antenna parameters such as the input impedance and current distribution. Starting with a convergence study followed by a parametric study is conducted to investigate the wall effects of the waveguide on the antenna performances.
In this paper, we first detail the integral equation formulation and the derivation of the necessary Green’s function for an infinite waveguide with the MOM method. The MOM-GEC is then presented and we present our structure developed using an equivalent circuit, followed by a comparative investigation of the electromagnetic behavior of dipole antenna in free space and inside an infinite rectangular waveguide as a function of the walls effect on the antenna performance. For example a convergence study of the input impedance is done.
2. Antenna Geometry
2.1. Thin Antenna Approximation (Pocklington Equation)
In [1] [3] - [5] , the antenna was modeled by a thin wire approximation (Pocklington equation). Considering the case of thin dipole antenna of length “L” and radius “a” placed in an infinite homogeneous medium, and subjected by an incident electric field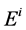 . The electric field at the surface of the antenna may be written as:
. The electric field at the surface of the antenna may be written as:
 (1)
(1)
where 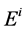 is the incident field and
is the incident field and  is the reflected field.
is the reflected field.
We may simplify the expression using the approximation of thin antenna (Pocklington equation), the current equation is:
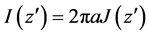 (2)
(2)
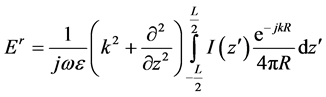 (3a)
(3a)
 (3b)
(3b)
By substituting the radiated electrical field expression, we have the Pocklington integral equation:
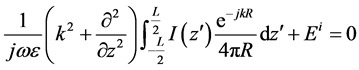 (4)
(4)
 (5)
(5)
(5) was the Green function in homogeneous and limited space with parameter 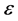 and
and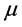 .
.
The current distribution along the dipole antenna is expressed as the sum of the samples current 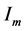 using a basis function
using a basis function 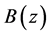 :
:
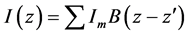
2.2. Dipole Antenna Modulation Using MoM Method
An antenna structure is broken into “segments” and the currents on the segments are then evaluated. The “moment” is numerically the size of the currents times the vector, describing the little segment (length and orientation).
A set of “basis functions” are assumed into which the current distributions are decomposed. The “MoM” starts from deriving the currents on each segment, or the strength of each moment, by using a coupling Green’s function [6] . This Green’s function incorporates electrostatic coupling between the moments, by knowing the spatial change of the currents, buildup of charges at points on the structure is computed.
3. MoM-GEC Formalism
Since the MoM method writes initial boundary conditions in form of integral equations defined on the discontinuity surface, it permits the reduction of the problem’s dimension. But, the resolution will become more complicated as the structure’s complexity increases. In this context, the equivalent circuits are introduced for the development of integral method formulation based on the transposition of field problems in generalized equivalent circuit that are simpler to treat [7] .
In fact, for alleviating the resolution of Maxwell’s equations, the method of Generalized Equivalent Circuit (MGEC) was proposed [7] - [10] in order to represent integral equations by equivalent circuits that express the unknown electromagnetic boundary conditions. The equivalent circuit presents a true electric image of the studied structures for describing the discontinuity and its environment.
In the discontinuity plane, the electromagnetic state is described by generalized test functions that are modeled by virtual sources not storing energy. An impedance operator or admittance operator that represents boundary conditions on each side of discontinuity surface expresses the discontinuity environment. However, the wave exciting the discontinuity surface is represented by a real field source or a real current source because it delivers energy.
4. Problem Formulation
4.1. Dipole Antenna Using MoM-GEC
Considering the circuit example showed in Figure 1. We can determine the current
![]()
Figure 1. Dipole antenna inside an infinite waveguide.
density lying in the metal part including the source domain and its associated field to verify the boundary conditions. Next, the integral equation is solved by applying the MOM method using Galerkin procedure.
The waveguide is infinite in both  and
and  directions and the equivalent circuit of this structure are shown in Figure 2.
directions and the equivalent circuit of this structure are shown in Figure 2.
Two sources, a virtual and a real one, are being involved in the formulation process. We trait the case that the virtual source is of current type and the real one is of electric field type. Mode sources, case of E-sources: all higher-order modes reflected at the first discontinuity of the structure being attenuated at the location of the source, they see an infinite waveguide.
The real source 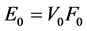 represents the excitation term associated to feeding element. This kind of source must also respect the property of the located element, which should be smaller than the wavelength. It has amplitude
represents the excitation term associated to feeding element. This kind of source must also respect the property of the located element, which should be smaller than the wavelength. It has amplitude ![]() and depends on special variables through
and depends on special variables through![]() . The function
. The function ![]() acts as the shape function, which ensures reliable expression for the voltage and current case of rectangular source
acts as the shape function, which ensures reliable expression for the voltage and current case of rectangular source![]() .
.
![]() is the virtual source defined on the metallic domain of the discontinuity surface and it is the problem unknown.
is the virtual source defined on the metallic domain of the discontinuity surface and it is the problem unknown. ![]() is expressed as a series of known test functions
is expressed as a series of known test functions ![]() weighted by unknown coefficients
weighted by unknown coefficients![]() :
:
![]()
Then the equivalent circuit of the studied structure is completed by addition the terminating operator![]() :
:
![]() (3)
(3)
The admittance operator ![]() is given by:
is given by:
![]() (4)
(4)
where ![]() or
or![]() ,
, ![]() being modal admittance of the nth mode of an infinite waveguide (IWG):
being modal admittance of the nth mode of an infinite waveguide (IWG):
![]()
Figure 2. Equivalent circuit representation of a dipole antenna.
![]() (5a)
(5a)
![]() (5b)
(5b)
Applying the Kirchhoff laws, we can deduce the relation between virtual, real sources and its duals, as given in the following equation system:
![]() (6)
(6)
Equation (6a) can be interpreted as the continuity relation of the current on the discontinuity surface. Equation (6b) expresses the continuity relation of the electric field. The current J is expressed in modal basis functions ![]() weighted by unknown coefficients
weighted by unknown coefficients![]() :
:
![]() (7)
(7)
Therefore, the application of the Galerkin’s method and Kirchhoff’s theorem leads to obtaining the simplified matrix representation as follows:
![]() (8)
(8)
where ![]() and
and ![]() .
.
4.2. Waveguide Walls Choice
The boundary conditions are defined on the contour of the structure. The better one can be chosen based on some criteria such as accuracy, rapidity and numerical convergence. The more the model basis respect the electromagnetic state of the real structure, the more it is adequate.
The use of virtual guide does not disturb the distribution of the diffracted electromagnetic field but physically choosing nature of this guide can be helpful to ensure a fast and precise calculation with better convergence of numerical results. The walls of the guide can be selected from the following types:
Electrical walls (EEEE).
Magnetic walls (MMMM).
An electric-magnetic combination (EMEM): two perfect magnetic walls (M) on the lateral side and two perfect electric ones (E) on the bottom and the top.
The electric-periodic walls (EPEP): two periodic walls (P) on the lateral side and two perfect electric ones (E) on the bottom and the top.
Each virtual waveguide type is associated to a modal basis![]() . The studied structure is invariant in y direction, and the waveguide is assured by a located source. Consequently the considered modal bases for every type are mentioned below:
. The studied structure is invariant in y direction, and the waveguide is assured by a located source. Consequently the considered modal bases for every type are mentioned below:
5. Results and Discussions
A comparative study is held between the different guide walls nature (electric, magnetic, electric magnetic combination and electric periodic combination) to validate our choice of the electric wall.
The electric walls are chosen since convergence is reached quickly in addition describes the environment we want to work with.
The results obtained show that the electrical walls simulate better the free space and convergence is reached quickly.
Concernant the virtual guide choice, all function basis (fmn) are littely equivalent, we may say that all guides atteind the same results at the convergence. However, according to the studied structures a base would be more appropriate in terms of convergence speed. To choose the introduced virtual guide type, we can respect either the real physical shape of current or that of the electric field (Figure 3 and Figure 4).
Figure 5 showed the convergence of the imnput impedance as a function of the
![]()
Figure 3. Current distribution for different guide wall nature.
![]()
Figure 4. Electric field distribution for different guide wall nature.
guide mode numbers for different test functions. Four walls nature are taken into account, we note that the convergence was atteinded quickly using the electric wall and allow us to modulate the radiation inside a car. Figure 5(a) presents the input impedance variation as a function of the test function number ![]() for different used basis function number
for different used basis function number![]() , which is fixed to 200 to ensure convergence. Studying the behavior of a dipole antenna both in free space and inside a rectangular infinite waveguide, it’s found that, MOM-GEC gives nearly the same results as that obtained in free space. Also a good study of convergence is elaborated to investigate the theoretical input impedance
, which is fixed to 200 to ensure convergence. Studying the behavior of a dipole antenna both in free space and inside a rectangular infinite waveguide, it’s found that, MOM-GEC gives nearly the same results as that obtained in free space. Also a good study of convergence is elaborated to investigate the theoretical input impedance ![]() evaluated by the MOM-GEC.
evaluated by the MOM-GEC.
The convergence was obtained for Nb = 200 and Ne = 24. The current and electric field distribution conforms to the theory and obey to the boundary conditions.
An important parameter that may affect the antenna response is the placement of the waveguide walls. We present in Figure 6 the current density distribution along the dipole antenna for different positions of electric walls. It’s found that, the current distribution is strongly affected by the lateral walls position. The separation distance have not any significant effect for a value that exceed a = 150 mm. In the following, the lateral walls positions are fixed at a = 150 mm and the b = 67 mm to insure the impact less of this parameter to further results.
Figure 7 and Figure 8 illustrate the electric field and current density evaluated by the MOM-GEC and obtained at convergence conforms to the theory with consideration to the boundary conditions.
As it is shown in Figure 9, integral method and MOM-GEC gives nearly the same current distribution for a dipole antenna of length 78.85 mm which corresponds to
![]() for an operating frequency f = 1.8 GHz.
for an operating frequency f = 1.8 GHz.
![]()
Figure 6. Current density distribution as a function of a walls distance.
![]()
Figure 7. 2D representation of the electric field density at f = 1.8 GHz.
![]()
Figure 8. 2D representation of the current density (A∙m−1) at f = 1.8 GHz.
![]()
Figure 9. Current distribution on a dipole antenna using integral method and MoM-GEC method for an antenna length L = 78.85 mm and operating at f = 1.8 GHz.
The current distribution with the integral method take approximately a triangular form, the current distribution with MOM-GEC is a half sinusoid for the same operating frequency.
6. Conclusion
A method for analyzing the electromagnetic problem of a dipole antenna radiating at 1.8 GHz inside a rectangular waveguide antenna has been presented. Validation of the method was made with free space. Numerical convergence tests were achieved. The electric walls are chosen since convergence is reached quickly and describes the environment working (inside a car).