Using a Multiverse Version of Penrose Cyclic Conformal Cosmology to Obtain Ergodic Mixing Averaging of Cosmological Information Transfer to Fix H Bar (Planck’s Constant) in Each New Universe Created during Recycling of Universes Due to CCC, Multiverse Style ()
1. Introduction
We refer the readers to an ergodic mixing procedure [1] - [3] as outlined in [4] by the author which is a way to have consistent mixing of “information” from the evolution to the death of universes, in terms of what is known as Penrose Cyclic conformal Cosmology [5] . What is also a bonus is that we also throw in by [6] a referral to the Alireza Sepehri, Ahmed Farag Ali supposition of reference [6] as to the formation of Wormholes for relic gravitons, as a way to argument the use of [1] - [4] .
2. A Brief Review as to the Use of the Material Given by Penrose, [5] Consistent with [4]
The key attribute as to the use of information and of the meta structure, is to use partition functions for a meta structure. Our idea is to use what is called a partition function [7] [8] for a universe, in order to
 . (1)
. (1)
However, there is non-uniqueness of information put into each partition function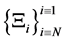 . Furthermore Hawking radiation from the black holes is collated via a strange attractor collection in the mega universe structure to form a new big bang for each of the N universes represented by
. Furthermore Hawking radiation from the black holes is collated via a strange attractor collection in the mega universe structure to form a new big bang for each of the N universes represented by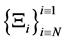 . Verification of this mega structure compression and expansion of information with a non-uniqueness of information placed in each of the N universes favors ergodic mixing treatments of initial values for each of N universe. How to tie in this energy expression, as in Equation (1) will be to look at the formation of a nontrivial gravitational measure as a new big bang for each of the N universes as by
. Verification of this mega structure compression and expansion of information with a non-uniqueness of information placed in each of the N universes favors ergodic mixing treatments of initial values for each of N universe. How to tie in this energy expression, as in Equation (1) will be to look at the formation of a nontrivial gravitational measure as a new big bang for each of the N universes as by 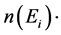 the density of states at a given energy Ei for a partition function. As is given in [4] we have
the density of states at a given energy Ei for a partition function. As is given in [4] we have
 . (2)
. (2)
Each of Ei identified with Equation (2) above, are with the iteration for N universes [1] . Then the following holds, namely, from [1] .
Claim 1:
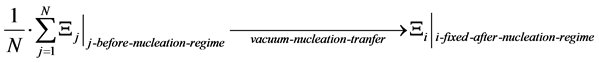 . (3)
. (3)
For N number of universes, with each  for j = 1 to N being the partition function of each universe just before the blend into the RHS of Equation (3) above for our present universe. Also, each of the independent universes given by
for j = 1 to N being the partition function of each universe just before the blend into the RHS of Equation (3) above for our present universe. Also, each of the independent universes given by 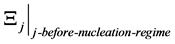 are constructed by the absorption of one to ten million black holes taking in energy. i.e. [1] . Furthermore, the main point is similar to what was done in terms of general ergodic mixing.
are constructed by the absorption of one to ten million black holes taking in energy. i.e. [1] . Furthermore, the main point is similar to what was done in terms of general ergodic mixing.
Claim 2:
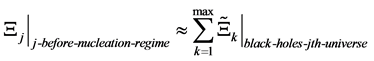 . (4)
. (4)
What is done in Claim 1 and Claim 2 is to come up with a protocol as to how a multi dimensional representation of black hole physics enables continual mixing of spacetime largely as a way to avoid the Anthropic principle, as to a preferred set of initial conditions. How can a graviton with a wavelength 10−4 the size of the universe interact with a Ker black hole, spatially. Embedding the BH in a multiverse setting may be the only way out.
Claim 1 is particularly important. Since it is a way to tie in, an averaging procedure for information as in the cycle per cycle re booting of the universe by Cyclic conformal cosmology, and this should be a way to insure that there is a through mixing of information, as to cosmological constants per cycle.
Claim 3, is our new one, which is important. We assume that for each partition function that each partition function as identified by Z, with F being the Hemoltz free energy that by [1] [8] [9]
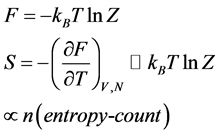 (5)
(5)
Here in the above, we make the following identification, namely that partition function Z, is related to Equation (2), and that the partition function of the universe, is mixed according to Equation (3). The last part of Equation (5) is a direct result of the Ng infinite quantum statistics hypothesis, and leads to an averaged out value for Equation (5) due to Equation (3). We then will close with the last part of this.
3. Conclusion, Using the Alireza Sepehri, Ahmed Farag Ali Supposition of Reference [5] as to the Formation of Wormholes for Relic Gravitons to Full Effect
In our document, we have labored as to use of initial conditions which may allow for use of a Tokamak to generate gravitational waves, and gravitons, of a frequency, commensurate with the relic graviton frequency of an initial universe setting in terms of measurable consequences today. To do so, we once again, restate what was said earlier.
Quote:
Here in the above, we make the following identification, namely that partition function Z, is related to Equation (2), and that the partition function of the universe, is mixed according to Equation (3).
End of quote.
Having said this how do we come up with a protocol, as to how to do this, in the early universe? A worthwhile suggestion as to incorporate both the early universe modification of the Heisenberg uncertainty principle [6] [10] and [7] [11] , and the possible avoidance of something from nothing conundrum which has bedeviled cosmologists ever since the Guth Big bang concept, is the examination of what reference [6] has to offer.
i.e. their seminal idea in [6] is to use the idea of wormholes. i.e. a worm hole which can do this has been brought up by L. Crowell, in [12] as a bridge between universes.
We wager that appropriate use of [6] may enable the use of this worm hole idea, and to avoid the conundrum of “something from nothing” which has been hotly contentious. Note that we can write our idea as of saying that gravitons may form information carriers from a prior universe to our own. To do this, we can refer back again to preliminary analogy with regards to Seth Lloyds universe as a quantum computer paper We begin, using the formula given by Seth Lloyd [13] 2001 with respect to the number of operations the “Universe” can “compute” during its evolution. To begin with, we use formula
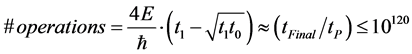 . (6)
. (6)
We assume that t1 = final time of physical evolution, whereas  seconds and that we can set an energy input via assuming in early universe conditions that
seconds and that we can set an energy input via assuming in early universe conditions that  and
and 
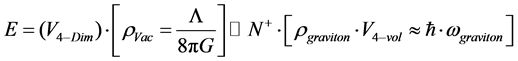 . (7)
. (7)
Furthermore, if we use the assumption that the temperature is close to 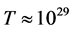 Kelvin initially, if we have an initial flux of gravitons as given through a worm hole as given in reference [13]
Kelvin initially, if we have an initial flux of gravitons as given through a worm hole as given in reference [13]
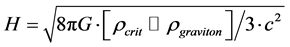
and
 . (8)
. (8)
Then
![]() (9)
(9)
i.e. the idea given in [6] and energy fluctuations may enable the transfer of information for the starting configuration of our universe, and this not through a singular big bang, but maybe through a nonsingular start to the universe as given by [14] .
Having said that, we also refer the reader to what the author did in reference [4] . i.e. in order to have a fully homogeneous start to the universe, the author in [4] generalized the Penrose supposition of a cyclic universe, to a multiverse, with repeated Ergodic mixing of initial components. The idea being that ergodic mixing through the multi universes, averaged out together, was a way to get rid of the possibility of having to use the “Darwinian” approach of only a few universes being survivable after being recycled. i.e. this Ergodic mixing is a way to insure that if one has the same Planck’s constant, ![]() for each recycled universe. And we bridge to the initial beginning of each universe, via Cyclic conformal cosmology, and mixing a worm hole construction of the sort given by [6] .
for each recycled universe. And we bridge to the initial beginning of each universe, via Cyclic conformal cosmology, and mixing a worm hole construction of the sort given by [6] .
In doing so, we lay the ground work for perhaps full investigation of what was brought up by Corda, in [15] as well as getting answers to the suppositions given by Dyson in [16] . And of course we will give more support to the research findings as given in [17] in maybe an early universe configuration.
Quote:
Moreover this would do away with the “baby universes” Darwinian hypothesis, set up by String theorists whom postulate that up to 10^1000 or so universes would be created, with only say 10^10 or so surviving(most dying off because of “improperly” set variance in the values of H bar (Planck’s constant).
End of quote.
Susskind in [18] is the foremost proponent of the Darwinian baby Universe picture, one which we state, due to the above, is not necessary.
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 11375279.