The Estimation of the Error at Richardson’s Extrapolation and the Numerical Solution of Integral Equations of the Second Kind ()

Subject Areas: Geology, Geophysics

1. Introduction
Numerical methods of the approached solution are attractive by the universality. In numerical methods three problems are put: obtaining enough exact solutions, accuracy control and algorithmic simplicity of procedures. Richardson’s extrapolation solves these problems. The first work of this theme was [1] . Since then many works (for example [2] ) are published and there is no necessity to do one more review. However, it is impossible to consider a theme exhausted. For example, in full enough handbook [3] , there is no even a mention of application of Richardson’s extrapolation to a solution of integral equations.
The purpose of this paper is to construct procedure of an estimation of an error at Richardson’s extrapolation and to apply it to a numerical solution of integral equations of the second kind of Volterra and Fredholm.
2. About Polynomial Richardson’s Extrapolation
We shall briefly remind an essence of Richardson’s extrapolation.
There are many problems from different sections of mathematics in which the difference between exact 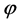 and approached
and approached  by solutions (an error of calculation of r) at sufficient smoothness of functions of a problem has expansion
by solutions (an error of calculation of r) at sufficient smoothness of functions of a problem has expansion
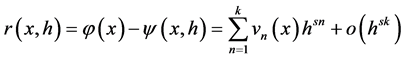 . (2.1)
. (2.1)
Magnitude h is usually a grid step.
We shall designate the approached solution as
 . (2.2)
. (2.2)
 is called as extrapolation of the zero order.
is called as extrapolation of the zero order.
Extrapolation of the 1-st order is obtained by elimination of the first term of expansion (2.1) by a linear combination of extrapolations of the zero order. Extrapolation of the j-st order is calculated on the recurrence formula
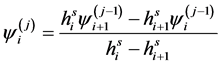 (2.3)
(2.3)
where usually is accepted .
.
In the end a table of extrapolations is obtained
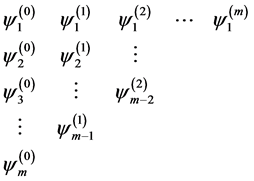 . (2.4)
. (2.4)
3. The Analysis of the Table of Extrapolations in Special Case
If magnitude h forms a geometrical progression
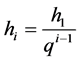 (3.1)
(3.1)
that (2.3) receives an aspect
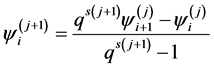 . (3.2)
. (3.2)
In this case from (3.2) and (2.1) we have
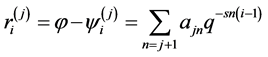 (3.3)
(3.3)
where lack of the top sign at the sum means that the remainder term is included in this sum.
We will name as the index of extrapolation 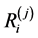 ratio
ratio
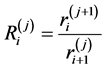 . (3.4)
. (3.4)
Extrapolation improves an exactitude  in comparison with
in comparison with ![]() when
when![]() .
.
From (3.3) follows
![]() (3.5)
(3.5)
where![]() .
.
Because ![]() we have an obvious relation
we have an obvious relation
![]() . (3.6)
. (3.6)
By means of the Formula (3.5) table ![]() is created.
is created.
Obviously, at a diminution h there occurs such moment when terms in expansion (3.3) start to decrease monotonically. We name this mode regular. If extrapolation becomes on a regular mode, the first term should bring the basic contribution in expansion (3.5). Then the relation should be observed
![]() . (3.7)
. (3.7)
And on the contrary: if the relation (3.7) is observed, we have a regular mode. Magnitude ![]() is almost constant in a table column. By means of the Formula (3.7) table
is almost constant in a table column. By means of the Formula (3.7) table ![]() is created.
is created.
Let’s enter magnitude
![]() (3.8)
(3.8)
and we shall define its meaning.
From (3.8), we have
![]() . (3.9)
. (3.9)
Substituting (3.9) in (3.2) we receive
![]() . (3.10)
. (3.10)
From (3.4), (3.6), (3.9) and (3.10) , we have
![]() . (3.11)
. (3.11)
Therefore, ![]() is estimation the index of extrapolation. By means of the Formula (3.8) table
is estimation the index of extrapolation. By means of the Formula (3.8) table ![]() is created.
is created.
By Formulas (3.6), (3.7), (3.11) and assumption ![]() the error estimation is
the error estimation is
![]() . (3.12)
. (3.12)
Starting from row (3.5) and definition (3.8), it is possible to establish that there is the expansion for ![]()
![]() (3.13)
(3.13)
where the first item has a basic meaning in a regular mode.
Then from (3.13) we receive the relation
![]() at
at ![]() (3.14)
(3.14)
on all table irrespective of an index j.
4. The Numerical Solution of Integral Equation of Volterra
Let’s consider integral equation of Volterra of the second kind.
![]() (4.1)
(4.1)
where ![]() and
and![]() .
.
This equation has an exact solution
![]() . (4.2)
. (4.2)
We shall designate the approximate solution of the Equation (4.1) at the calculation of integrals on a trapezoidal rule with extrapolation by![]() .
.
Procedure of a solution of integral equation of Volterra of the second kind with application of the trapezoidal rule is known (for example [3] ). At the calculation of integrals by the trapezoidal rule s = 2. At q = 2 each previous set of points contains in the subsequent set and it enables application of extrapolation. Then (3.3) receives the form
![]() (4.3)
(4.3)
and (3.2) receives the form
![]() . (4.4)
. (4.4)
It is sometimes more convenient to use “direct” formulas
![]() (4.5)
(4.5)
which come out by sequential application of the Formula (4.4).
Let’s consider (4.1) on a piece x = 0 ÷ 2.5 with step![]() . Below tables of extrapolations and other magnitudes according to formulas of the previous section are reduced. Calculations were made with 15-th significant digits, but for convenience of reading in tables of number are approximated.
. Below tables of extrapolations and other magnitudes according to formulas of the previous section are reduced. Calculations were made with 15-th significant digits, but for convenience of reading in tables of number are approximated.
By means of the Formula (3.5) table ![]() is created.
is created.
By means of the Formula (3.7) table ![]() is created.
is created.
By means of the Formula (3.8) table ![]() is created.
is created.
The analysis of tables leads to the important conclusions. From Table 1 and Table 2 follows that ![]() is the most exact value. It is visible from Table 3 that the Formula (3.7) is satisfactorily satisfied. From Table 4 follows,
is the most exact value. It is visible from Table 3 that the Formula (3.7) is satisfactorily satisfied. From Table 4 follows,
![]()
Table 1. Table of extrapolation ![]() in the point x = 2.5. The exact magnitude is shown by bold type.
in the point x = 2.5. The exact magnitude is shown by bold type.
that ![]() depends from j a little at everyone i. Now it is possible to make an estimation of the error of
depends from j a little at everyone i. Now it is possible to make an estimation of the error of ![]() at x = 2.5. From (3.12) we have
at x = 2.5. From (3.12) we have
![]() . (4.6)
. (4.6)
The true error is![]() .
.
We have received the precision solution in isolated points. It is interesting to find good interpolation function and to receive a solution in the analytical form. Let’s make uniform set from ![]() with the step 0.1 (26 points). Interpolation by continuous fractions (the command Thiele Interpolation in the package Curve Fitting of the program Maple) was better than interpolation by cubic splines. Interpolation by continuous fractions we shall
with the step 0.1 (26 points). Interpolation by continuous fractions (the command Thiele Interpolation in the package Curve Fitting of the program Maple) was better than interpolation by cubic splines. Interpolation by continuous fractions we shall
designate ![]() and
and ![]() serves as control value. These results are presented in Table 5.
serves as control value. These results are presented in Table 5.
The Equation (4.1) for area ![]() can be written down in the form.
can be written down in the form.
![]() . (4.7)
. (4.7)
The Equation (4.7) defines the solution at ![]() if function
if function ![]() is known at
is known at![]() .
.
5. The Numerical Solution of Integral Equation of Fredholm
The equation is considered
![]() (5.1)
(5.1)
which has the exact solution![]() .
.
Procedure of a solution of integral equation of Fredholm of the second kind with application of the trapezoidal
![]()
Table 5. Interpolation ![]() and exact solution
and exact solution![]() . At x = 2.488 interpolation has the largest error.
. At x = 2.488 interpolation has the largest error.
rule is also known (for example [3] ). We keep designations of the previous section. We shall produce tables (also with a rounding) without explanations as the analysis of tables is invariable (Tables 6-9).
From (3.12) we have the estimation of the error of![]() . The true error is
. The true error is![]() .
.
The remark. Trapezoidal rule is the scheme of 2-nd order of exactitude and s = 2 in expansions (2.1) and (3.3). For a calculation of interpolations of zero order it is possible to use Simpson’s formula (the formula of 4-th order of exactitude). For Simpson’s formula expansion on even degrees is kept, but in (2.1) and (3.3) the first term vanishes. Formally it means: in (2.1) and (3.3) we do replacement![]() , but it is necessary to preserve indexes of terms
, but it is necessary to preserve indexes of terms ![]() and
and![]() . Formulas (2.1) and (3.3) get the form (at s = 2)
. Formulas (2.1) and (3.3) get the form (at s = 2)
![]() (5.2)
(5.2)
and
![]() . (5.3)
. (5.3)
If to begin calculations from Simpson’s formula then in the formula (3.2) it is necessary to replace![]() ; but it does not concern magnitudes
; but it does not concern magnitudes ![]() as we keep the indexing the order of extrapolation. The formula (3.2) receives the form
as we keep the indexing the order of extrapolation. The formula (3.2) receives the form
![]() (5.4)
(5.4)
and “direct” formulas receive the kind
![]() . (5.5)
. (5.5)
The important note: by means of the formula (3.2), it is easy to establish that Simpson’s formula is extrapolation of 1-st order of a trapezoidal rule and there is no real necessity to use Simpson’s formula. Let’s remind that application of any schemes of a high exactitude demands high smoothness of functions.
6. Conclusion
Trapezoidal rule with Richardson’s extrapolation is the effective method of a solution of integral equations of the second kind, and with application of interpolation we receive a solution in an analytical aspect. In this case the table of extrapolations enables to make a good estimation of an error of solution. The received solution possesses a high exactitude and can be the standard for other methods of a solution of the equation.
![]()
Table 6. Table of extrapolation ![]() in the point x = 1. The exact magnitude is shown by bold type.
in the point x = 1. The exact magnitude is shown by bold type.