Convergence Analysis of General Version of Gauss-Type Proximal Point Method for Metrically Regular Mappings ()
Received 7 January 2016; accepted 17 July 2016; published 20 July 2016

1. Introduction
We are concerned in this study with the problem of finding a point  satisfying
satisfying
 (1)
(1)
Martinet [1] proposed the following algorithm for the first time for applying it to convex optimization by considering a sequence of scalars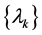 , which are different from zero:
, which are different from zero:
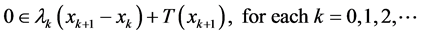 (2)
(2)
Rockafellar [2] thoroughly explored the method (2) in the general framework of maximal monotone inclu- sions. In particular, Rockafellar ( [2] , Theorem 1) shows that when  is an approximate solution of (2) and T is maximal monotone, then for a sequence of positive scalars
is an approximate solution of (2) and T is maximal monotone, then for a sequence of positive scalars 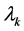 the iteration (2) generates a sequence
the iteration (2) generates a sequence 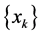 which is weakly convergent to a solution of (1) for any starting point
which is weakly convergent to a solution of (1) for any starting point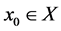 . In [3] , Aragón Artacho et al. have been presented the general version of the proximal point algorithm (GPPA) (see Algorithm 1), for the case of nonmonotone mappings, for solving the inclusion (1).
. In [3] , Aragón Artacho et al. have been presented the general version of the proximal point algorithm (GPPA) (see Algorithm 1), for the case of nonmonotone mappings, for solving the inclusion (1).
Let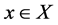 . The subset of X, denoted by
. The subset of X, denoted by![]() , is defined by
, is defined by
![]() (3)
(3)
Thus we have the following algorithms which have been presented by Aragón Artacho et al. [3] :
Note that, for a starting point near to a solution, the sequences generated by Algorithm 1 are not uniquely defined and not every sequence is convergent. The results obtained in [3] guarantee the existence of one sequence, which is convergent. Therefore, from the viewpoint of numerical computation, we can assume that these kinds of methods are not suitable in practical application. This drawback motivates us to introduce a method “so- called” general version of Gauss-type proximal point algorithm (GG-PPA). The difference between Algorithm 1 and our proposed Algorithm 2 is that the GG-PPA generates sequences, whose every sequence is convergent, but this does not happen for Algorithm 1. Thus we propose here the GG-PPA as follows:
We observe, from Algorithm 2, that
1) if ![]() and then we assume
and then we assume ![]() a Hilbert space, this algorithm reduces to the classical pro- ximal point algorithm defined by (2).
a Hilbert space, this algorithm reduces to the classical pro- ximal point algorithm defined by (2).
2) if![]() , Algorithm 2 is equivalent to the classical Gauss-type proximal point method, which has been introduced by Rashid et al. [4] .
, Algorithm 2 is equivalent to the classical Gauss-type proximal point method, which has been introduced by Rashid et al. [4] .
A large number of authors have been studied on proximal point algorithm and have also found applications of this method to specific variational problems. Most of the study on this subject have been concentrated on various versions of the algorithm for solving inclusions involving monotone mappings, and specially, on monotone variational inequalities (see in [5] - [8] ). Spingarn [9] has been studied first weaker form of monotonicity and for details see in [10] .
There have a large study on local convergence analysis about Algorithm 1 (cf. [3] [11] [12] ), but there is no semilocal analysis for Algorithm 1. A huge number of contributions have been studied on semilocal analysis for the Gauss-Newton method (cf. [4] [13] - [16] ). In [4] , Rashid et al. have given a semilocal convergence analysis for the classical Gauss-type proximal point method. As our best knowledge, there is no study on semilocal analysis for Algorithm 2. Therefore we conclude that the contributions presented in this study are seems new.
In the present paper, our aim is to study the semilocal convergence for the GG-PPA defined by Algorithm 2. The metric regularity property and Lipschitz-like property for set-valued mappings are mainly used in our study. The main results are convergence analysis, established in section 3, which based on the attraction region around the initial point and provide some sufficient conditions ensuring the convergence to a solution of any sequence generated by Algorithm 2. As a consequence, local convergence results for GG-PPA are obtained.
This paper is arranged as follows. In Section 2, some necessary notations, notions and preliminary results are presented. In Section 3, we consider the GG-PPA which is introduced in Section 1 and by using the concept of metric regularity property for the set valued mapping T, we will show the existence and present the convergence of the sequence generated by Algorithm 2. In Section 4, we present a numerical experiment to validate the semilocal convergence of Algorithm 2. In the last Section, we will give a summary of the major results to close our paper.
2. Notations and Preliminary Results
In the whole paper, we assume that X and Y are Banach spaces. Let F be a set-valued mapping from X into the subsets of Y, denoted by![]() . Let
. Let ![]() and
and![]() . The closed ball centered at x with radius r is denoted by
. The closed ball centered at x with radius r is denoted by![]() . The domain
. The domain![]() , the inverse
, the inverse ![]() and the graph
and the graph ![]() of F are respectively defined by
of F are respectively defined by
![]()
![]()
and
![]()
All the norms are denoted by![]() . Let
. Let ![]() and
and![]() . The distance from x to A is defined by
. The distance from x to A is defined by
![]()
while the excess from the set C to the set A is defined by
![]()
From [4] , we recall the following definition of metric regularity for set-valued mapping.
Definition 1 Let ![]() be a set-valued mapping and let
be a set-valued mapping and let![]() . Let
. Let ![]() and
and![]() . Then F is said to be
. Then F is said to be
1) metrically regular at ![]() on
on ![]() with constant
with constant ![]() if
if
![]() (4)
(4)
2) metrically regular at ![]() if there exist constants
if there exist constants ![]() and
and ![]() such that F is metrically regular at
such that F is metrically regular at ![]() on
on ![]() with constant
with constant![]() .
.
The infimum of the set of values ![]() for which (4) holds is the modulus of metric regularity, denoted by
for which (4) holds is the modulus of metric regularity, denoted by![]() . The absence of metric regularity at
. The absence of metric regularity at ![]() for
for ![]() corresponds to
corresponds to![]() . The inequality (4) has direct use in providing an estimate for how far a point x is from being a solution to the generalized equation
. The inequality (4) has direct use in providing an estimate for how far a point x is from being a solution to the generalized equation ![]() and the expression
and the expression ![]() measures the residual when
measures the residual when![]() .
.
Recall the definition of Lipschitz-like continuity for set-valued mapping from [17] . This notion was introduced by Aubin in [18] and has been studied extensively.
Definition 2 Let ![]() be a set-valued mapping and let
be a set-valued mapping and let![]() . Let
. Let ![]() and
and![]() . Then
. Then ![]() is said to be Lipchitz-like at
is said to be Lipchitz-like at ![]() on
on ![]() with constant M if the following inequqlity hold:
with constant M if the following inequqlity hold:
![]() (5)
(5)
The following result establish the equivalence relation between metric regularity of a mapping F at ![]() and the Lipschitz-like continuity of the inverse
and the Lipschitz-like continuity of the inverse ![]() at
at![]() , which is obtained from the idea in [19] [20] .
, which is obtained from the idea in [19] [20] .
Lemma 1 Let ![]() be a set valued mapping and
be a set valued mapping and![]() . Let
. Let![]() , then F is metrically regular at
, then F is metrically regular at ![]() on
on ![]() if and only if its inverse
if and only if its inverse ![]() is Lipschitz-like at
is Lipschitz-like at ![]() on
on ![]() with constant
with constant ![]() such that
such that
![]()
We recall the following statement of Lyusternik-Graves theorem for metrically regular mapping from [21] . This theorem plays an important role in the theory of metric regularity and proves the stability of metric regularity of a generalized equation under perturbations. For its statement, we use that a set ![]() is locally closed at
is locally closed at ![]() if there exists
if there exists ![]() such that the set
such that the set ![]() is closed.
is closed.
Lemma 2 Consider a mapping ![]() and any
and any ![]() at which
at which ![]() is locally closed. Let F be metrically regular at
is locally closed. Let F be metrically regular at ![]() for
for ![]() with constant
with constant![]() . Consider also a function
. Consider also a function ![]() which is Lipschitz continuous at
which is Lipschitz continuous at ![]() with Lipschitz constant
with Lipschitz constant ![]() such that
such that![]() . Then the mapping
. Then the mapping ![]() is metric-
is metric-
ally regular at ![]() for
for ![]() with constant
with constant![]() .
.
We finished this section with the following lemma, which is known as Banach fixed point theorem proved in [22] .
Lemma 3 Let ![]() be a set-valued mapping. Let
be a set-valued mapping. Let![]() ,
, ![]() and
and ![]() be such that
be such that
![]() (6)
(6)
and
![]() (7)
(7)
Then ![]() has a fixed point in
has a fixed point in![]() , that is, there exists
, that is, there exists ![]() such that
such that![]() . If
. If ![]() is additionally single-valued, then the fixed point of
is additionally single-valued, then the fixed point of ![]() in
in ![]() is unique.
is unique.
3. Convergence Analysis of GG-PPA
In this section, we assume that ![]() is a set-valued mapping with locally closed graph at
is a set-valued mapping with locally closed graph at ![]() such that T is metrically regular at
such that T is metrically regular at ![]() with constant
with constant![]() . Let
. Let ![]() be a (single-valued) function such that
be a (single-valued) function such that![]() , which is Lipschitz continuous in a neighborhood O of 0 with a Lipschitz constant
, which is Lipschitz continuous in a neighborhood O of 0 with a Lipschitz constant ![]() Let
Let ![]() and define a mapping
and define a mapping ![]() by
by
![]() (8)
(8)
Then we obtain the following equivalence
![]() (9)
(9)
In particular,
![]() (10)
(10)
Let ![]() and let
and let![]() . Since
. Since ![]() is Lipschitz continuous on
is Lipschitz continuous on![]() , app- lying the Lyusternik-Graves theorem (see Lemma 2) we assume that the mapping
, app- lying the Lyusternik-Graves theorem (see Lemma 2) we assume that the mapping ![]() is metrically regular at
is metrically regular at
![]() with constant
with constant![]() , that is, by Lemma 1 we have the following inequality
, that is, by Lemma 1 we have the following inequality
![]() (11)
(11)
Write
![]() (12)
(12)
Then
![]() (13)
(13)
The following lemma plays an important role for convergence analysis of the GG-PPA, which is due to [23] .
Lemma 4 Suppose that ![]() is metrically regular at
is metrically regular at ![]() on
on ![]() with constant
with constant ![]() such that (12) and (13) are satisfied. Let
such that (12) and (13) are satisfied. Let ![]() and
and![]() . Then
. Then ![]() is Lipschitz-like at
is Lipschitz-like at ![]() on
on ![]() with constant
with constant![]() , that is,
, that is,
![]()
For our convenience, we consider a sequence of functions ![]() with
with ![]() which are Lipschitz continuous in a neighbourhood O of 0, the same for all k, with Lipschitz constants
which are Lipschitz continuous in a neighbourhood O of 0, the same for all k, with Lipschitz constants ![]() satisfying
satisfying
![]() (14)
(14)
We rewrite the mapping ![]() in (8) by substituting
in (8) by substituting ![]() instead of g as follows:
instead of g as follows:
![]() (15)
(15)
Since ![]() by (14), then by Lyusternik-Graves theorem (see Lemma 2) and Lemma 1 we obtain that the mapping
by (14), then by Lyusternik-Graves theorem (see Lemma 2) and Lemma 1 we obtain that the mapping ![]() is Lipschitz-like at
is Lipschitz-like at ![]() on
on ![]() with constant
with constant ![]() satisfying (11) and hence we have
satisfying (11) and hence we have
![]() (16)
(16)
Furthermore, we define, for each![]() , the mapping
, the mapping ![]() by
by
![]() (17)
(17)
and the set-valued mapping ![]() by
by
![]() (18)
(18)
Then
![]() (19)
(19)
The main result of this study given as follows, which provides some sufficient conditions ensuring the convergence of the GG-PPA with initial point![]() .
.
Theorem 1 Suppose ![]() and that
and that ![]() is metrically regular at
is metrically regular at ![]() on
on ![]() with constant
with constant![]() , and let
, and let ![]() be defined in (12). Let
be defined in (12). Let ![]() and
and ![]() be such that
be such that
a)![]() ,
,
b)![]() ,
,
c)![]() .
.
Suppose that
![]() (20)
(20)
Then there exists some ![]() such that any sequence
such that any sequence ![]() generated by Algorithm 2 with initial point in
generated by Algorithm 2 with initial point in ![]() converges to a solution
converges to a solution ![]() of (1), that is,
of (1), that is, ![]() satisfies that
satisfies that![]() .
.
Proof. Let
![]() (21)
(21)
Then by assumption (b), (21) gives us
![]() (22)
(22)
Assumption (c) and (20) allow us to take ![]() so that
so that
![]() (23)
(23)
We will proceed by mathematical induction and show that Algorithm 2 generates at least one sequence and any sequence ![]() generated by Algorithm 2 satisfies the following assertions
generated by Algorithm 2 satisfies the following assertions
![]() (24)
(24)
and
![]() (25)
(25)
for each![]() . Define
. Define
![]() (26)
(26)
Since![]() , by assumption (b) and (c), we have
, by assumption (b) and (c), we have
![]() (27)
(27)
It is trivial that (24) is true for![]() . For showing that (25) is true for
. For showing that (25) is true for![]() , we need to prove that
, we need to prove that ![]() exists, that is,
exists, that is,![]() . We will prove
. We will prove ![]() by applying Lemma 3 to the mapping
by applying Lemma 3 to the mapping ![]() with
with
![]() . Let us check that both assertions (6) and (7) of Lemma 3 are hold with
. Let us check that both assertions (6) and (7) of Lemma 3 are hold with ![]() and
and![]() . Noting that
. Noting that
![]() by (10). Then by the mapping
by (10). Then by the mapping ![]() in (18) and the definition of excess e, we have
in (18) and the definition of excess e, we have
![]() (28)
(28)
(noting that![]() ). Now, by the choice of
). Now, by the choice of![]() , we have
, we have
![]() (29)
(29)
Since![]() , by the fact
, by the fact ![]() in assumption (a) and
in assumption (a) and ![]() in assumption (c), for each
in assumption (c), for each![]() , (29) implies that
, (29) implies that
![]() (30)
(30)
that is, for each![]() ,
,![]() . In particular,
. In particular,
![]() (31)
(31)
Hence by using (31) and Lemma 1 for Lipschitz-like property in (28), we have
![]()
This shows that assertion (6) of Lemma 3 is satisfied. Now, we show that the assertion (7) of Lemma 3 is satisfied. Let![]() . Then by assumption (a) and (27), we have
. Then by assumption (a) and (27), we have ![]()
and ![]() by (30). By assumed Lipschitz-like property of
by (30). By assumed Lipschitz-like property of![]() , we have
, we have
![]() (32)
(32)
Applying (19) in (32), we obtain
![]() (33)
(33)
Then by (14), (33) reduces to
![]()
This implies that the assertion (7) of Lemma 3 is also satisfied. Since both assertions (6) and (7) of Lemma 3 are fulfilled, we can deduce there exists a fixed point ![]() such that
such that![]() , which translates to
, which translates to![]() , that is,
, that is, ![]() and hence
and hence![]() .
.
Now, we show that (25) is hold for![]() .
.
Note that ![]() by assumption (a). Then (13) is valid for (14). Since
by assumption (a). Then (13) is valid for (14). Since ![]() is Lipschitz-like at
is Lipschitz-like at ![]() on
on![]() , it follows from Lemma 4 that the mapping
, it follows from Lemma 4 that the mapping ![]() is Lipschitz-like at
is Lipschitz-like at ![]() on
on
![]() with constant
with constant ![]() for each
for each![]() . In particular,
. In particular, ![]() is Lipschitz-like at
is Lipschitz-like at ![]() on
on ![]() with constant
with constant ![]() as
as ![]() by assumption (a) and the choice of
by assumption (a) and the choice of![]() . Furthermore, assumptions (a) and (c) imply that
. Furthermore, assumptions (a) and (c) imply that
![]() (34)
(34)
It seems that![]() . Then by Lemma 1 we can say that the mapping
. Then by Lemma 1 we can say that the mapping ![]() is metrically regular on
is metrically regular on
![]() relative to
relative to ![]() with constant
with constant![]() . Thus by applying Lemma 1, we have
. Thus by applying Lemma 1, we have
![]() (35)
(35)
and (23) implies that
![]() (36)
(36)
Then from (16) and using (36), we obtain that
![]() (37)
(37)
From Algorithm 2 and using (21) and (37), we obtain that
![]() (38)
(38)
This implies that (25) is hold for![]() .
.
Suppose that the points ![]() have been obtained, and (24) and (25) are true for
have been obtained, and (24) and (25) are true for![]() . We will show that there exists a point
. We will show that there exists a point ![]() such that (24) and (25) also hold for
such that (24) and (25) also hold for![]() . Since (24) and (25) are true for each
. Since (24) and (25) are true for each![]() , we have the following inequality
, we have the following inequality
![]() (39)
(39)
This reflects that (24) holds for![]() . Now with almost the same argument as we did for the case when
. Now with almost the same argument as we did for the case when![]() , we can find that the mapping
, we can find that the mapping ![]() is also Lipschitz-like at
is also Lipschitz-like at ![]() on
on ![]() with
with
constant![]() . Then by applying again Algorithm 2, we have
. Then by applying again Algorithm 2, we have
![]() (40)
(40)
This shows that (25) holds for![]() . Therefore, the proof is completed.
. Therefore, the proof is completed.
In the particular case, when ![]() is a solution of (1), that is,
is a solution of (1), that is, ![]() , Theorem 1 is reduced to the following corollary, which gives the local convergence of the sequence generated by the GG-PPA defined by Algorithm 2.
, Theorem 1 is reduced to the following corollary, which gives the local convergence of the sequence generated by the GG-PPA defined by Algorithm 2.
Corollary 1 Suppose that ![]() and that
and that ![]() satisfies
satisfies ![]() and that
and that ![]() is metrically regular at
is metrically regular at
![]() with constant
with constant![]() . Let
. Let ![]() be such that
be such that ![]() and suppose that
and suppose that
![]() (41)
(41)
Then there exists some ![]() such that any sequence
such that any sequence ![]() generated by Algorithm 2 with initial point in
generated by Algorithm 2 with initial point in ![]() converges to a solution
converges to a solution ![]() of (1), that is,
of (1), that is, ![]() satisfies that
satisfies that![]() .
.
Proof. Since ![]() is metrically regular at
is metrically regular at![]() , there exist constants
, there exist constants![]() ,
, ![]() and
and ![]() such that
such that ![]() is metrically regular at
is metrically regular at ![]() on
on ![]() with constant
with constant![]() . Then, for each
. Then, for each![]() , one has that
, one has that
![]() (42)
(42)
Let ![]() be such that
be such that![]() . Choose
. Choose ![]() such that
such that ![]() and
and ![]() Then
Then
![]() (43)
(43)
and
![]() (44)
(44)
Thus we can choose ![]() such that
such that
![]() (45)
(45)
Now it is routine to check that inequalities (a)-(c) of Theorem 1 are hold. Thus Theorem 1 is applicable to complete the proof of the corollary.
4. Numerical Experiment
We will provide, in this section, a numerical example to validate the semilocal convergence results of GG-PPA.
Example 1 Let![]() . Define a set-valued mapping T on
. Define a set-valued mapping T on ![]() by
by![]() . Consider a sequence of Lipschitz continuous function
. Consider a sequence of Lipschitz continuous function ![]() with
with![]() , which is
, which is
defined by![]() . Then Algorithm 2 generates a sequence which is converges to
. Then Algorithm 2 generates a sequence which is converges to![]() .
.
It is obvious from the statement that T is metrically regular at ![]() and
and ![]() is Lipschitz continuous on the neighborhood of 0 with Lipschitz constant
is Lipschitz continuous on the neighborhood of 0 with Lipschitz constant![]() . Consider
. Consider![]() . Then from (3), we have that
. Then from (3), we have that
![]()
On the other hand, if ![]() we obtain that
we obtain that
![]()
Thus from (40), we obtain that
![]()
For the given values of![]() , we see that
, we see that![]() . Thus, this implies that the sequence generated
. Thus, this implies that the sequence generated
by Algorithm 2 converges linearly. Then the following Table 1, obtained by using Mat lab program, indicates that the solution of the generalized equation is 0.5 when![]() .
.
Moreover, in the case when![]() , we can sketch the following Figure 1:
, we can sketch the following Figure 1:
5. Conclusions
In this study, we have established semi-local and local convergence results for the general version of Gauss-type proximal point algorithm for solving generalized equation under the assumptions that![]() , a sequence of functions
, a sequence of functions ![]() with
with ![]() which is Lipschitz continuous in a neighbourhood O of the origin
which is Lipschitz continuous in a neighbourhood O of the origin
![]()
Table 1. Finding a solution of generalized equation.
and T is metrically regular. Moreover, we have presented a numerical experiment to validate the semilocal convergence result for Algorithm 2. For the case where![]() , the question, whether the results are true for GG-PPA, is a little bit complicated. However, from the proof of the main theorem, one sees that all the results obtained in the present paper remain true provided that, for any
, the question, whether the results are true for GG-PPA, is a little bit complicated. However, from the proof of the main theorem, one sees that all the results obtained in the present paper remain true provided that, for any![]() , the following implication holds:
, the following implication holds:
![]()
To see the detail proof of the above implication, one can refer to [17] .
Acknowledgements
We thank the editor and the referees for their comments. Research of this work is funded by the Ministry of Science and Technology, Bangladesh, grant No. 39.009.002.01.00.053.2014-2015/EAS-19. This support is greatly appreciated.