Do the Two Operations Addition and Multiplication Commute with Each Other? ()

Subject Areas: Applied Physics
1. Introduction
Zermelo-Fraenkel set theory with the axiom of choice, commonly abbreviated ZFC, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. It has a single primitive ontological notion, that of a hereditary well-founded set, and a single ontological assumption, namely that all individuals in the universe of discourse are such sets. ZFC is a one-sorted theory in first-order logic. The signature has equality and a single primitive binary relation, set membership, which is usually denoted Î. The formula 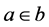 means that the set a is a member of the set b (which is also read, “a is an element of b” or “a is in b”). Most of the ZFC axioms state that particular sets exist. For example, the axiom of pairing says that given any two sets a and b there is a new set
means that the set a is a member of the set b (which is also read, “a is an element of b” or “a is in b”). Most of the ZFC axioms state that particular sets exist. For example, the axiom of pairing says that given any two sets a and b there is a new set 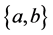 containing exactly a and b. Other axioms describe properties of set membership. A goal of the ZFC axioms is that each axiom should be true if interpreted as a statement about the collection of all sets in the von Neumann universe (also known as the cumulative hierarchy). The me- tamathematics of ZFC has been extensively studied. Landmark results in this area that is established the in- dependence of the continuum hypothesis from ZFC, and of the axiom of choice from the remaining ZFC axioms [1] . Mach literature concerning above topic can be seen in Refs. [2] - [18] .
containing exactly a and b. Other axioms describe properties of set membership. A goal of the ZFC axioms is that each axiom should be true if interpreted as a statement about the collection of all sets in the von Neumann universe (also known as the cumulative hierarchy). The me- tamathematics of ZFC has been extensively studied. Landmark results in this area that is established the in- dependence of the continuum hypothesis from ZFC, and of the axiom of choice from the remaining ZFC axioms [1] . Mach literature concerning above topic can be seen in Refs. [2] - [18] .
We use the validity of Addition and Multiplication. Here we aim to provide an example that the two opera- tions Addition and Multiplication do not commute with each other. All analyses are performed in a finite set of natural numbers.
2. The Two Operations Addition and Multiplication Do Not Commute with Each Other
Assume all axioms of Zermelo-Fraenkel set theory with the axiom of choice is true.
Let us start with a singleton set
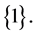 (1)
(1)
We treat here Addition. We have
 (2)
(2)
Thus we obtain 2. By using the obtained 2, we have
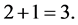 (3)
(3)
Thus we obtain 3. By repeating this method for an even number time, we have
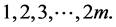 (4)
(4)
By repeating this method, we have
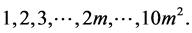 (5)
(5)
Thus we have the following finite set of natural numbers
 (6)
(6)
By using the set (6), we discuss that the two operations Addition and Multiplication do not commute with each other.
We consider a value V which is the sum of the results of trials. Result of trials is 1 or 2. We assume the number of 2 is equal to the number of 1. The number of trials is 2 m. We have
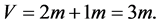 (7)
(7)
We derive the possible value of the product 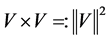 of the value V. It is
of the value V. It is
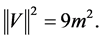 (8)
(8)
We assign the truth value “1” for the following proposition
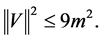 (9)
(9)
We have
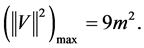 (10)
(10)
The value  which is the sum of the results of trials is given by
which is the sum of the results of trials is given by
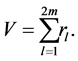 (11)
(11)
We assume that the possible value of the actually happened results  is 1 or 2. We have
is 1 or 2. We have
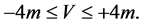 (12)
(12)
The same value is given by
![]() (13)
(13)
We only change the labels as ![]() and
and![]() . The possible value of the actually happened results
. The possible value of the actually happened results ![]() is 1 or 2. We have
is 1 or 2. We have
![]() (14)
(14)
and
![]() (15)
(15)
Here![]() . By using these facts we derive a necessary condition for the value given in (11). We derive the possible value of the product
. By using these facts we derive a necessary condition for the value given in (11). We derive the possible value of the product ![]() of the value V given in (11). We have the following under the assumption that the two operations Addition and Multiplication commute with each other.
of the value V given in (11). We have the following under the assumption that the two operations Addition and Multiplication commute with each other.
![]()
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
The step (16) to (17) is OK. The step (17) to (18) is valid under the assumption that the two operations Addition and Multiplication commute with each other. The step (18) to (19) is true since we have only changed the label as![]() .
.
The above inequality (19) is saturated since
![]() (22)
(22)
and
![]() (23)
(23)
We derive a proposition concerning the value given in (11) under the assumption that the possible value of the actually happened results is 1 or 2, that is![]() . We derive the following proposition
. We derive the following proposition
![]() (24)
(24)
We do not assign the truth value “1” for the two propositions (10) and (24) simultaneously. We are in a contradiction. Thus we have to give up the assumption that the two operations Addition and Multiplication commute with each other.
3. Conclusion
In conclusions, we have used the validity of Addition and Multiplication. We have provided an example that the two operations Addition and Multiplication do not commute with each other. All analyses have been performed in a finite set of natural numbers.