Demand Elasticity of Capacity Offered for Urban Rail Transport ()
Received 9 February 2016; accepted 27 June 2016; published 30 June 2016

1. Introduction
The peak hour demand in Urban Rail Transport is usually significantly higher than the demand in nonpeak hours. Conventionally more capacity in terms of number of vehicles per hour is offered in the peak hours to meet the demand. The measures to increase the supply are termed as Supply Side Measures [1] to meet the demand. The additional capacity not only addresses the peak hour congestion but also attracts new traffic as people find it easier to use services with additional capacity. The supply side measures refer to transit service quality factors such as availability, convenience, speed and comfort. Improvement in services spurs the growth of the transport demand. However, the increase of supply is limited by the design capacity of the system beyond which any increase in the supply requires major investment to enhance the capacity of the system. The supply management tools are applied incrementally to match the increasing demand over the time. The supply management tools deployed in URT are listed Figure 1 below.
2. Supply Side Measures [2]
The capacity offered may be enhanced by deploying the following measures individually or in combination.
2.1. Increase in Trians
The carrying capacity of a URT system is determined by passenger capacity of the trains passing through a point in an hour. The carrying capacity can be simply increased by introducing more trains in an hour if system permits.
2.2. Increase in Cars per Train
The carrying capacity can also be increased by adding more cars per train even without increasing the number of trains provided system permits addition of more cars. DMRC has progressively increased the number of cars per train from 4 cars to 8 Cars now at Line 2, Line 3 & 4.
![]()
Figure 1. Supply side measures for urban transport.
2.3. Signalling System up Gradation
The Signalling System may be upgraded to allow the trains at closure headways. The Paris Metro, London Underground have adopted the most modern Communication Based Train Control Systems (CBTC) with driverless Train Operations to improve the frequency of the trains and to increase the capacity of the system.
2.4. Increase in Frequency of the Trains
The number of trains per hour (frequency) can also be improved by removing the bottlenecks in the system like reducing the terminal reversal time, increase in speed of the trains, minimisation of dwell time at stations, optimisation in time tabling.
As per UITP article (PTI 3/2013) on “Better Fare Regulation for Public Transport” an increase in capacity by 10% on fixed network through frequency enhancements or larger trains, the ridership is likely to increase by 5%.
2.5. Station Capacity Enhancement
The stations especially those near CBD may not be able to cater to the ever growing traffic demand. The capacity of the station can be increased by adding more area to the station building, relocating some of the activities outside the station like ticketing activities etc.
2.6. Limitations of Supply Side Management Tools
The supply side solutions can be adopted only to the extent of capacity of the infrastructure. For example, the length of the platforms of the BG lines of Delhi Metro, India can accommodate 8 cars only as the maximum length of the train. Further, any addition beyond capacity needs improvement in track, signalling, rolling stock, manpower which involves huge capital investment. The supply side solutions always results into suboptimal utilisation of the assets as demand during non-peak hours remain below the capacity of the system.
3. Efficacy of Supply Management Measures
The supply management measures are found to be effective in only in short run to cater the demand. The increase in supply also results in growth of demand in long run and more often it is found the demand outpaces the supply over the time. So the efficacy of supply management measures is limited in long term perspective.
4. Supply Management Model to Assess Demand
As discussed above, the demand is a function of supply.
Demand = f (supply).
The demand elasticity [3] [4] w.r.t services is defined as % increase in demand for 1% change in the supply i.e. es = % change in demand/% change in supply.
If, the current demand is Ri passenger/hour per direction and the carkms have been increasef from Ci to Cf, the increase in demand would be:
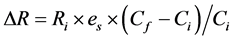
The final demand would be
 (1)
(1)
Here,
es is demand elasticity with respect to capacity.
Ri is the current demand in passenger/hour per direction.
Rf is the modified demand in passenger/hour per direction after increasing the capacity offered.
∆R is change in demand due to increase in capacity offered.
Ci is number of trains per hour or carkms per hour at present.
Cf is number of trains per hour or carkms per hour after increase.
5. Case of Delhi Metro Rail Corporation (Dmrc), India: Elasticity W.R.T Capacity Offered
Delhi Metro is witnessing double digit growth in ridership ever since it started its operations in 2002. Delhi Metro has taken several steps in the past to match the demand by augmenting the supply of accommodation (cars) by way of increasing number of trains in peak hours, busy section, improving the speed of the trains, dwell time rationalisation, reducing terminal reversal time, adopting Automatic Train Operations. All these measures are supply side measures aiming at increasing the supply of accommodation to match the demand.
Delhi Metro has designed its system to accommodate 8 car length trains in Broad Gauge Lines (Red, yellow & blue lines) and 6 car length trains in Standard Gauge lines (Violet and Green lines). Delhi Metro started its services with 4 car length trains in all the lines. Over the time with increase in demand, the train length in BG lines are being increased to 6 cars /8 cars per train.
Here in this study, the effect of conversion of 4 car length trains to 6 car/8 car length trains on ridership in Line 2 (yellow line) of DMRC has been analyzed. Till 2010, 50 number of 4 car length trains have been operated in the peak hours in Line 2 of the DMRC. The Capacity augmentation in line 2 started from Feb 2011 with introduction of 6 car trains. By Oct 2012 all 4c trains were converted into 6C trains. The conversion of 6c trains into 8c trains started Dec 2012. As on Oct, 2015, 33 trains have been converted into 8 c.
The ridership of the line increases on account of natural growth and on account of increase in the capacity offered. The ridership and capacity data for line 2 of Delhi Metro for three years (2011, 2012 & 2013) have been analyzed to estimate the elasticity of demand w.r.t services offered. The following assumptions have been made in determination of elasticity:
1) On the basis of growth in demand on other lines, it is assumed that there is a 7% natural growth of ridership.
2) The balance growth is on account of increase in capacity.
The Table 1 presents the ridership & capacity offered in Line 2 for three years:
% increase in capacity in 2012 w.r.t 2011 = 19.06----------------------------------------(A)
% increase in ridership in 2012 due to additional capacity = 14.43---------------------(B)
Elasticity w.r.t service in 2012 = 0.757------------------------------------------------------C = (B/A)
% increase in capacity in 2013 w.r.t 2012 = 27.58-----------------------------------------(D)
% increase in ridership in 2013 due to additional capacity = 7.368----------------------(E)
Elasticity w.r.t service in 2013 = 0.267-------------------------------------------------------F = (E/D)
Average eklasticity w.r.t capacity = 0.512---------------------------------------------------(C + F)/2
![]()
Table 1. Ridership & capacity offered in line 2 of DMRC for three years.
As per UITP article (PTI 3/2013) [5] on “Better Fare Regulation for Public Transport” an increase in capacity by 10% on fixed network through frequency enhancements or larger trains, the ridership is likely to increase by 5%. i.e. Es = 0.5.
A value of 0.512 of Es for DMRC is comparable to the international estimates [6] .
The value of Es for first year of increase in supply is 0.757 and for second year, it is just 0.267. The drastic reduction in value of Es in second year is attributed to decreasing marginal utility of capacity enhancement in second year.
6. Application of Supply Management Model for Delhi Metro
The supply management model as discussed in IV above has been applied for yellow line, the busiest line of Delhi Metro as presented in Table 2 and Figure 2 for illustration purpose:
 .
.
Evidently as supply is increased, the ridership in terms of demand (Pax/hour) also increases proportionally depending upon the value of demand elasticity with respect to services. Todd Litman [3] has estimated the value of elasticity with respect to service in the range of 0.5 to 0.7 in short run (less than two years) i.e. a 10% increase in trains per hour would result into 5% to 7% increase in the ridership. The increase in ridership of DMRC with enhancement of services is in line with the studies available in the literature.
![]()
Figure 2. Relationship between demand & supply for DMRC.
![]()
Table 2. Application of supply management model for delhi metro.
*Equation (1) under para 4.0 has been used to determine the demand.
7. Conclusion
The supply side measures can be effective in short term till the capacity of the system is utilized. However, in short term also, the increase in supply spurs the growth of the demand which makes supply side measures only partially effective. The study reveals that a 10% increase in supply results into around 5% increase in ridership of urban rail transport which mean that there is only 5% relief in congestion. In long term any additional capacity beyond the design capacity would require huge capital investment [6] . There is a need to deploy demand side measures [7] [8] such as differential fares (higher fares in peak hours), congestion charges, staggered timings of offices/schools/institutes etc. to ease peak hour congestion. An optimum combination of supply and demand side measures would perhaps be the best way to address peak hour congestion in Urban Rail Transport.