Received 3 April 2016; accepted 21 May 2016; published 24 May 2016

1. Introduction
The problem of convergence of a doubly indexed sequence presents some interesting phenomena related to the order of taking iterated limits as well as subsequences where one index is a function of the other. Convergence of a double sequence in the sense of Pringsheim is a strong enough condition to allow us to characterize the behavior of the iterated limits as well as the limits of ordinary sequences induced by collapsing the two indices into one according to a suitable functional dependence (e.g. re-index 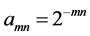 by setting
by setting 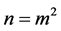 to obtain
to obtain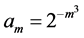 ). We will show that an unconditional converse establishing convergence in the Pringsheim sense from properties of the iterated limits is not obtainable.
). We will show that an unconditional converse establishing convergence in the Pringsheim sense from properties of the iterated limits is not obtainable.
We can easily extend the notion of Pringsheim convergence of numerical sequences to pointwise convergence in the Pringsheim sense for functions. Our main goal is to investigate the doubly indexed sequence of real functions of the form  in this context. One iterated limit of this sequence, namely
in this context. One iterated limit of this sequence, namely
 , is a well-known example of the construction of the Dirichlet “salt-and-pepper” function
, is a well-known example of the construction of the Dirichlet “salt-and-pepper” function
 . Recall
. Recall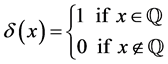 . In addition to establishing a theorem on Pringsheim convergence which is
. In addition to establishing a theorem on Pringsheim convergence which is
useful in its own right, we will be able to conclude that  does not converge pointwise in this sense. Moreover, it will be shown that there are irrational numbers for which the ordinary sequence
does not converge pointwise in this sense. Moreover, it will be shown that there are irrational numbers for which the ordinary sequence 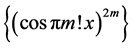 does not converge to zero.
does not converge to zero.
2. Background
The German mathematician Alfred Pringsheim formulated the following definition of convergence for double sequences in 1897 [1] .
Definition 1: Given the doubly indexed sequence , we say it converges to the limit L if for every preassigned
, we say it converges to the limit L if for every preassigned ![]() there exists a
there exists a ![]() such that
such that ![]() whenever
whenever![]() . This situation will be denoted by
. This situation will be denoted by![]() .
.
In this definition, it is understood that m and n are to exceed ![]() independently. Specifically, there should be no functional relationship between m and n, such as
independently. Specifically, there should be no functional relationship between m and n, such as![]() , for example. The definition lends itself to an intuitively appealing visual. We will call the semi-infinite set of grid points
, for example. The definition lends itself to an intuitively appealing visual. We will call the semi-infinite set of grid points ![]() below and to the right of
below and to the right of ![]() a
a ![]() Pringsheim square:
Pringsheim square:
![]()
In this array the rows represent fixed m with n increasing, and the columns represent fixed n with m increasing. The column to the extreme right records ![]() and the row at the bottom records
and the row at the bottom records![]() , whenever these limits exist. For arbitrary
, whenever these limits exist. For arbitrary ![]() the double limit L exists if there is a
the double limit L exists if there is a ![]() such that the absolute difference between L and any term in the
such that the absolute difference between L and any term in the ![]() Pringsheim square is strictly less than
Pringsheim square is strictly less than![]() . The iterated limits
. The iterated limits ![]() and
and ![]() may or may not be equal. A trivial
may or may not be equal. A trivial
but illustrative case is given by the double sequence![]() . The array with iterated limits is:
. The array with iterated limits is:
![]()
Observing that the iterated limits exist and are equal to zero, but the double limit in the Pringsheim sense does not even exist, since for any ![]() there are terms with
there are terms with ![]() such that
such that ![]() and
and![]() . Note also that if we violate the condition that m and n exceed
. Note also that if we violate the condition that m and n exceed ![]() independently by setting
independently by setting![]() ,
, ![]() exists and equals 1. This example immediately dashes any hope of establishing a Fubini-like result where if the two iterated limits exist and are equal then the double limit in the Pringsheim sense exists and is the same.
exists and equals 1. This example immediately dashes any hope of establishing a Fubini-like result where if the two iterated limits exist and are equal then the double limit in the Pringsheim sense exists and is the same.
A more optimistic case is this:
![]()
This array shows that a double sequence can be Pringsheim convergent, and although none of the row ![]() or column
or column ![]() partial limits equal the Pringsheim limit (1), the respective row-first
partial limits equal the Pringsheim limit (1), the respective row-first ![]() and column-first
and column-first ![]() iterated limits can equal the Pringsheim limit. Motivated by this example we formulate a theorem that connects Pringsheim convergence to the existence and equality of the associated iterated limits.
iterated limits can equal the Pringsheim limit. Motivated by this example we formulate a theorem that connects Pringsheim convergence to the existence and equality of the associated iterated limits.
3. Main Theorem
Theorem 1: Let ![]() be a double sequence of real numbers with Pringsheim limit
be a double sequence of real numbers with Pringsheim limit ![]() . If for some
. If for some ![]() both the partial limit
both the partial limit ![]() exists for
exists for ![]() and the partial limit
and the partial limit ![]() exists for
exists for![]() , then the iterated limits
, then the iterated limits ![]() and
and ![]() exist and are equal to L.
exist and are equal to L.
Proof: Without restriction of generality, consider the column sequence formed by the partial limits Am for m > M. Fix ε > 0. We claim that![]() . Since
. Since ![]() converges to L in the sense of Pring-
converges to L in the sense of Pring-
sheim, there exists ![]() such that
such that ![]() implies
implies![]() . Increase
. Increase![]() , if warranted, so that
, if warranted, so that
![]() . This defines a
. This defines a ![]() Pringsheim square for which all of the row and column partial lim-
Pringsheim square for which all of the row and column partial lim-
its exist and every amn within the square differs absolutely from L by less than![]() . Now
. Now
![]() , and since
, and since![]() , we may stipulate that
, we may stipulate that![]() . It is clear that
. It is clear that![]() , and our claim that
, and our claim that ![]() is established. The same argu-
is established. The same argu-
ment mutatis mutandi shows that![]() . +
. +
In view of the array we have used to visualize the Pringsheim definition, let us call a double subsequence ![]() southeastern if
southeastern if![]() , where
, where ![]() is strictly monotone increasing. The terminology is suggested by the fact that for any
is strictly monotone increasing. The terminology is suggested by the fact that for any ![]() Pringsheim square the double subsequence
Pringsheim square the double subsequence ![]() will eventually enter and stay inside the part of the square below (south) and to the right (east) of aKK. The ordinary subsequences where either m or n are held constant (the horizontal or vertical subsequences in the array) do not have this property. Clearly, every southeastern subsequence can be converted to an ordinary subsequence.
will eventually enter and stay inside the part of the square below (south) and to the right (east) of aKK. The ordinary subsequences where either m or n are held constant (the horizontal or vertical subsequences in the array) do not have this property. Clearly, every southeastern subsequence can be converted to an ordinary subsequence.
Corollary 1a: If ![]() is a double sequence of real numbers, then
is a double sequence of real numbers, then ![]() if and only if every southeastern subsequence of amn converges to L.
if and only if every southeastern subsequence of amn converges to L.
Proof: (Necessity) Suppose every southeastern subsequence of amn converges to L. Fix ![]() and assume for the sake of contradiction that
and assume for the sake of contradiction that![]() . Then every
. Then every ![]() Pringsheim square contains an amn such that
Pringsheim square contains an amn such that![]() . Construct a southeastern subsequence of “bad” terms as follows: Let K = 1. Choose a term
. Construct a southeastern subsequence of “bad” terms as follows: Let K = 1. Choose a term ![]() in the (1)-Pringsheim square (the entire array) such that
in the (1)-Pringsheim square (the entire array) such that![]() . Now select
. Now select ![]() in the
in the ![]() -Pringsheim square so that
-Pringsheim square so that![]() . Likewise select a3 from the
. Likewise select a3 from the ![]() -Pringsheim square and so forth recursively. By the manner of construction, i > j requires mi > mj and ni > nj, so the resulting subsequence is certainly southeastern. Moreover,
-Pringsheim square and so forth recursively. By the manner of construction, i > j requires mi > mj and ni > nj, so the resulting subsequence is certainly southeastern. Moreover, ![]() cannot converge to L. The contradiction establishes necessity.
cannot converge to L. The contradiction establishes necessity.
(Sufficiency) Suppose ![]() is a double sequence of real numbers with
is a double sequence of real numbers with![]() . Fix
. Fix ![]() and consider the southeastern subsequence
and consider the southeastern subsequence![]() . By Pringsheim convergence, there exists a
. By Pringsheim convergence, there exists a ![]() Pringsheim square such that
Pringsheim square such that ![]() for all
for all![]() . Choose
. Choose ![]() and determine
and determine![]() . If
. If![]() , we may choose
, we may choose ![]() such that
such that ![]() by the isotonicity of
by the isotonicity of![]() . In any case, by relabelling, if necessary, we may arrange that
. In any case, by relabelling, if necessary, we may arrange that![]() . Thus
. Thus ![]() belongs to the
belongs to the ![]() Pringsheim square that constrains the absolute difference between
Pringsheim square that constrains the absolute difference between ![]() and L to be less than
and L to be less than![]() . Again by the isotonicity of
. Again by the isotonicity of
![]() ,
, ![]() for
for![]() . Hence the southeastern sequence
. Hence the southeastern sequence ![]() converges to L. +
converges to L. +
Let us formulate a definition of pointwise Pringsheim convergence of functions so that we have a basis for studying![]() . In particular, we will consider
. In particular, we will consider![]() .
.
Definition 2: The doubly indexed sequence of real functions ![]() converges pointwise in the Pringsheim sense if whenever x is fixed, the resulting numerical sequence converges in the regular Pringsheim sense (definition 1). This situation will be denoted by
converges pointwise in the Pringsheim sense if whenever x is fixed, the resulting numerical sequence converges in the regular Pringsheim sense (definition 1). This situation will be denoted by![]() .
.
If a doubly indexed sequence of functions were simply pointwise convergent and the iterated limits did not commute, the limit function would be ill-defined. Our definition along with Theorem 1 resolves this issue.
Corollary 1b: Theorem 1 applies to the pointwise limits of doubly indexed sequences of functions with amn replaced by ![]() and L replaced by
and L replaced by![]() .
.
Proof: Fix x and use definition 2. +
4. Dirichlet Function
Consider [2] [3] ![]() for
for![]() . If
. If![]() , and
, and ![]() is not an integer, then
is not an integer, then
![]() , and consequently
, and consequently![]() . However, once m is sufficiently large,
. However, once m is sufficiently large, ![]() becomes and remains an integer, hence
becomes and remains an integer, hence ![]() for those cases. It follows that
for those cases. It follows that ![]() for rational x. On the other hand, if
for rational x. On the other hand, if![]() , the quantity
, the quantity ![]() is never an integer for any m, hence
is never an integer for any m, hence![]() , and consequently
, and consequently ![]() for all m, so
for all m, so![]() . Defining
. Defining
![]() , we have
, we have ![]() for
for![]() . Dirichlet’s function
. Dirichlet’s function ![]() is
is
everywhere discontinuous, and a fanciful image of its “graph” has given rise to the name “salt-and-pepper” function. It is often used as an example of a function that is Lebesgue integrable but not Riemann integrable (although integrable in the generalized Riemann sense).
Dirichlet’s function turns out to be an example of a Baire class 2 function. Recall that Baire class 0 consists of functions that are continuous. Baire class 1 functions are pointwise limits of sequences of Baire class 0 functions. In general, a Baire class ![]() function is the pointwise limit of a sequence of functions from the union of all Baire classes with indices less than
function is the pointwise limit of a sequence of functions from the union of all Baire classes with indices less than![]() , where the class index is allowed to range over the countable ordinals. The fact that the Dirichlet function cannot be expressed as the limit of a sequence of continuous functions will play a key role in establishing our claim that
, where the class index is allowed to range over the countable ordinals. The fact that the Dirichlet function cannot be expressed as the limit of a sequence of continuous functions will play a key role in establishing our claim that ![]() does not converge in the Pringsheim sense.
does not converge in the Pringsheim sense.
5. Baire’s Category Theorem (BCT)
René-Louis Baire proved the seminal theorem that bears his name in 1899 as part of his doctoral dissertation [4] . He introduced the famously bland terminology Category 1 for meager sets and Category 2 for non-meager sets. Recall that a meager set is a countable union of nowhere-dense sets, which in turn are sets whose closures have void interiors. Non-meager sets are all the others. BCT states (in one formulation) that complete metric spaces must be non-meager. We use this fact in the following:
Theorem 2: The southeastern sequence ![]() induced from
induced from ![]() by setting
by setting ![]() does not converge pointwise to Dirichlet’s function
does not converge pointwise to Dirichlet’s function ![]() on
on![]() .
.
Proof: Suppose to the contrary that ![]() for
for![]() . For fixed m,
. For fixed m, ![]() is continuous on
is continuous on![]() . It can be shown (see [5] , for example) that for any topological space X, if
. It can be shown (see [5] , for example) that for any topological space X, if ![]() is a sequence in
is a sequence in![]() , and f is the pointwise limit of
, and f is the pointwise limit of![]() , the set of discontinuities of f cannot be arbitrary, but must in fact be a meager set. Now,
, the set of discontinuities of f cannot be arbitrary, but must in fact be a meager set. Now, ![]() is a pointwise limit of continuous functions, and therefore converges to a Baire class 1 function, which by the preceding must have a meager set of discontinuities on
is a pointwise limit of continuous functions, and therefore converges to a Baire class 1 function, which by the preceding must have a meager set of discontinuities on![]() . However, the set of discontinuities of
. However, the set of discontinuities of ![]() is all of
is all of![]() . By BCT, since
. By BCT, since ![]() is a complete metric space, it is non-meager. Therefore
is a complete metric space, it is non-meager. Therefore ![]() cannot be a Baire class 1 function and the result follows from the contradiction. +
cannot be a Baire class 1 function and the result follows from the contradiction. +
Note that for infinitely many values of x (![]() will do)
will do)![]() , but the point of the theorem is that it cannot be true for all
, but the point of the theorem is that it cannot be true for all![]() .
.
Theorem 3: The double sequence ![]() is not pointwise convergent in the Pringsheim sense.
is not pointwise convergent in the Pringsheim sense.
Proof: Suppose to the contrary that ![]() for
for![]() . By Theorem 1 the iterated pointwise limits and the pointwise limits of all induced southeastern sequences should be
. By Theorem 1 the iterated pointwise limits and the pointwise limits of all induced southeastern sequences should be![]() . However we know from the discussion above regarding Dirichlet’s function that the iterated limit
. However we know from the discussion above regarding Dirichlet’s function that the iterated limit ![]() on
on![]() , but the southeastern sequence
, but the southeastern sequence ![]() does not have this limit function by Theorem 2. The contradiction establishes that the pointwise Pringsheim limit
does not have this limit function by Theorem 2. The contradiction establishes that the pointwise Pringsheim limit ![]() does not exist. +
does not exist. +
Theorems 2 and 3 allow us to conclude that “curious cosines” exist. These have the property that they form a numerical sequence where each term is absolutely less than one and the successive terms are raised to arbitrarily high powers, but they nevertheless avoid converging to zero. The apparently intimate coördination between the arguments of the cosines and the powers to which they are raised prevents this.
Theorem 4: (Curious Cosines Exist) There exists an irrational ![]() such that
such that![]() .
.
Proof: For![]() ,
, ![]() , as eventually the tail of the sequence is constantly 1. If every irrational
, as eventually the tail of the sequence is constantly 1. If every irrational ![]() resulted in 0 as a limit, we would have the Dirichlet function, contradicting Theorem 2. Hence there must exist an
resulted in 0 as a limit, we would have the Dirichlet function, contradicting Theorem 2. Hence there must exist an ![]() such that
such that![]() . +
. +
6. Postscript
The subject of Pringsheim convergence seems to have been neglected over the years. Only recently has the subject of Pringsheim convergence of series been revived [6] , with new results paralleling the single index theory and correcting previous errant results.