Application of Parametric-Based Framework for Regionalisation of Flow Duration Curves ()
Received 26 January 2016; accepted 14 May 2016; published 17 May 2016

1. Introduction
In Nigeria, the government has embarked on exploitation of alternative sources of energy based on domestic renewable resources, e.g., solar and hydropower. The geographic and climatic conditions of some regions in Nigeria endow them with a high potential for hydropower generation. The development of large hydropower schemes in Nigeria faces difficulties due to environmental and resettlement problems just like the case with many developing countries. Since most selected sites for small hydropower projects are normally located on small streams where flow records are rarely available, computation methods must be developed to estimate the streamflow and the power potential of the site.
The flow duration curve (FDC) is a common method to estimate the streamflow for small hydropower development. It is used to assess the anticipated availability of flow over time and consequently the power and energy on site. A typical example of this was that of [1] where a power duration curve was derived from the combination of FDC and power discharge rating curve. To achieve this, other times series such as monthly, weekly, or daily flow data can be used to construct the relationship (e.g. [2] ). However, [3] opined that monthly streamflow data satisfy the basic data requirement for water resource projects. Considering this therefore, regionalisation of FDC can be done to achieve qualitative results, especially for places where there is dearth of comprehensive data base. In the studies by [4] FDC methods were divided into two groups: (i) mathematical equations or statistical distributions to fit FDC constructed from gauged data, whereas on the other hand, (ii) FDCs can be developed by establishing regression equation between the discharge of some specific exceedance percentages (e.g., 10%, 20%, 30%…, and 90%) with the catchment characteristics or annual average flow. Similarly, [5] classified regionalisation procedures into three categories: (i) statistical, (ii) parametric, and (iii) graphical approaches. The first category view FDC as the complement of the cumulative frequency distribution while the second and the third are respectively procedures which do not make any connection between FDC and the probability theory. Considering this, according to [6] , regionalisation technique is preferable in small-scale water projects because of cost and time implications. Generally, it suffices to note however that regional flow duration curves can be constructed by using the available data of the regionalisation techniques, which include stream flow data recorded at other existing gauging stations in the same region.
Against the backdrop of the foregoing discussion, the objective of the study therefore, is to develop a simple model based on probability distributions to estimate the monthly FDC at ungauged sites in the Upper Niger River basin of Nigeria, which has a high potential to contribute to the development of small hydropower projects.
2. Materials and Methods
2.1. Hydrology of the Basin and Data Assembly
The Upper Niger River Basin, Nigeria consist of sub-basins (e.g., Gurara, Gbako, and Kaduna, among others) which lie in the intermediate zone between semi-arid climate in the north and sub-humid climate in the south; the climate is influenced by the seasonal movement of the Inter tropical Convergence Zone, which results in wet and dry seasons. Rain starts in April (early rains) or May and lasts till October, with the peak rainfall occurring in September. The dry season lasts between November and March with the mean annual rainfall of some locations in the Basin as follows: 1300 mm (Minna), 1500 mm (Abuja), 1600 mm (Kafanchan), 1250 mm (Kaduna) and 1400 mm (Jos). The mean monthly maximum and minimum temperatures in the basins are 37.3˚C and 19.7˚C, respectively, with the hottest months being February, March and April.
For this study, a total of 7 gauged sites (Kaduna, Shiroro, Kachia, Izom, Baro, Zungeru and Agaie) in the three selected rivers within the river basin controlling an area ranging from 900km2 to 6200 km2 were used. In this case, records of average monthly gauged flows for the respective rivers were obtained from Niger State and Kaduna State Water Boards as well as Power Holding Company of Nigeria (PHCN); these records were for gauging stations at Kachia and Izom (Gurara sub-basin), Kaduna, Shiroro and Zungeru (Kaduna sub-basin), and Agaie (Gbako sub-basin). Figure 1 shows the gauging stations whose records were employed for this study.
2.2. Study Protocol
The study is primarily patterned after some studies such as [7] , [8] , and [1] , as well as [9]
1) Development of Regular Flow Duration Curves and Regional Models
![]()
Figure 1. Location map showing the various gauging stations within Upper Niger River Basin.
In the development of the FDC, catchment area was taken as the major characteristics in all the models; this choice was informed by the lack of available information on other catchment characteristics of interest. The FDCs were constructed by re-assembling the flow time series values in the decreasing order of magnitude assigning flow values to class intervals and counting the number of occurrences (time steps) within each class intervals. Accumulated class frequencies were then calculated and expressed as a percentage of the total number of time steps in the record. The lower limit of every discharge class interval was plotted against the percentage points and then the discharges of exceedance percentage QP% (p = 1, 5, 10, …, 99) for each catchment were calculated using specific FDC. Based on the submissions of [5] , parametric method was employed in the regionalisation protocol. In this approach, analytical functions were fitted to empirical flow duration curves in order to regionalise them. To do this, three basic probability distributions were considered; i.e., logarithmic, power and exponential.
Mathematical models of the flow duration curves were developed based on the logarithmic, power, and exponential transformation framework. Resulting from this, the following equations were employed corresponding to the respective framework; that is, Equations (1)-(6)
 (1)
(1)
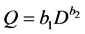 (2)
(2)
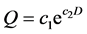 (3)
(3)
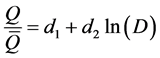 (4)
(4)
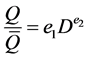 (5)
(5)
 (6)
(6)
where, a?f are the coefficients, Q is the discharge; D is the Duration and  is mean discharge.
is mean discharge.
Figure 2 shows examples of the fitted plots for (i) logarithmic, (ii) exponential, and (iii) power models
By using regression analysis, the models as represented by Equations (1)-(3) and (4)-(6) were fitted to each set of paired values of Q versus D and  versus D, respectively. The models with the Coefficient of Determination (R2) closest to 1 were considered best fit with values of R2 of Equations (1)-3), being statistically equal to that of Equations (4)-(6), respectively. Table 1 shows R2 for the models for each station.
versus D, respectively. The models with the Coefficient of Determination (R2) closest to 1 were considered best fit with values of R2 of Equations (1)-3), being statistically equal to that of Equations (4)-(6), respectively. Table 1 shows R2 for the models for each station.
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 2. Examples of measured flow duration curves and the fitted lines from logarithmic, power and exponential models for Kaduna station.
![]()
Table 1. Regression coefficient or Coefficient of determination (R2) for the three models.
2) Regional Flow Duration Models
Three sub-basins of the Upper Niger River basin were selected for the study. These sub-basins, for the purposes of this study were (1) Kaduna, (2) Gbako, (3) and Gurara sub-basins. Details of stations (name, area and the period of the records) are as given in Table 2. The records for the seven stations were divided into two for the development of the FDC and regionalisation procedures. This split sampling approach required that some segments of the data were used for calibration and validation; to achieve this, five stations and the remaining two were used for calibration and validation, respectively.
Since the logarithmic and exponential models gave the highest values of average R2, model development was created from the data in Table 2 by establishing the relationship between drainage area and coefficients from the logarithmic and exponential models. The spatial variation coefficients were correlated with the drainage area. Table 3 shows the respective values of the coefficients a1, a2 and d1, d2 from the logarithmic models in Equations (1) and (4) and that of coefficients c1, c2 and f1, f2 from the exponential models in Equations (3) and (6), respectively for each of the study locations. The plots for the determination of the regionalised parameters are as shown in Figures 3-6; these parameters so determined were then employed in the regionalisation framework.
![]()
Figure 3. Relationship between coefficients a1, a2 and drainage area at sub-basin level.
![]()
Figure 4. Relationship between coefficients c1, c2 and drainage area.
![]()
Table 2. Data segmentation for model development and simulation.
![]()
Figure 5. Relationship between coefficients of d1, d2 and drainage area at sub-basin level.
![]()
Figure 6. Relationship between coefficients of f1, f2 and drainage area.
![]()
Table 3. Determined coefficient values for logarithmic and exponential models.
In doing so, the drainage area (A) and the coefficients were plotted to identify the relationships; The relationships were simply established by methods of least squares (i.e., Figure 1). The straight-line equations of the coefficients are as in Equations (7)-(14).
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
The straight-line coefficients (j1 to j4, k1 to k4, l1 to l4 and m1 to m4) were further determined using regression analysis. Table 4 shows the computed values for these coefficients.
The calculated basin values were inserted into Equations (7) and (8) for the dimensioned logarithmic and exponential models and (12) to (13) for the dimensionless Logarithmic and exponential models in order to compute the discharges (Q) corresponding to percent of time (D) at intervals increasing 1% each time up to 100%; for each station, these were computed and compared between the results from the Logarithmic and exponential models to find the best fitted model. Based on the re-parameterisation, Equations (15)-(18) were obtained; i.e., for the respective logarithmic and exponential schema.
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
The estimation of each sub-basin’s representative average flow (Q) in Equations (20) and (21) was performed by analysing the relationship between mean annual flow and drainage area, as in Equation (19)
![]() (19)
(19)
where A is drainage area in km2; “a” as well as “b” are constants, their values are as presented in Table 5. Based on the re-parameterisation procedure, the regionalised models were obtained according as in Equations (20)- (21).
![]()
Table 4. Regionalised parameter values.
![]()
Table 5. Coefficients a, b and Q for each station.
![]() (20)
(20)
![]() (21)
(21)
where l1 to l4, m1 to m4, and a, b, are constants, respectively
3) Model Calibration and validation for flow prediction
To ascertain the adequacy or otherwise of the regional models, model calibration and validation were carried out. The accuracy of regional models was examined by using the measured discharges. In order to do this, measured and simulated results were compared in terms of root mean square relative error (ER)
![]() (22)
(22)
where D is the percent of time between 1% to 100%, QDc is the computed discharge at any percent of time; QDm is the measured discharge at any percent of time. Using the coefficients J1 to J4, K1 to K4, l1 to l4 and m1 to m4, the constants a, b and the drainage area of each station, the predicted discharges at 1% to 100% with interval 1% for each step or percentage of time (D) were determined from Equations (15)-(18).
3. Results and Discussion
3.1. Flow Variability and Issues of Consistency
Table 6 shows the variability in the flow patterns for the stations considered; in this case, variability is on the basis of low flow pattern. The low flow index though indicates that there may be some level of spatial correlation between the stations but whether this sparingly seeming correlation could provide for robust long-term prediction of flow in the ungauged stations becomes a matter of interest. This is imperative considering consistency related issues of the secondary data used for model calibration and validation since the prediction capability of the model is wholly depended on model conceptual assumptions and proper parameter estimation; in this context, the data length readily becomes a culprit. Because of the short length of data employed here, effective long-term generalisations may not really be practicable due to inherent vagaries. As noticed in Table 6, the high values of the low variation could be attributable to short falls in rainfall pattern coupled with problems of seasonality vis-à-vis climate change dynamics. In the overall, this could translate to long-term change in flow pattern; for this, the viable explanation for the foreseeable change pattern could be attributable to deleterious effects of anthropogenic activities and variations in the hydroclimatology of the Basin writ large.
3.2. Performance of Regular and Regionalised FDCs
It is evident from the development of the regular FDCs that both the logarithmic and exponential probability distribution models were appropriate for the understanding of the flow dynamics of the Basin. The findings here are not in accord with that of [7] and [8] . These authors, based on their findings proposed the adoption of exponential and cubic probability distribution models, respectively. This difference points to the fact that any wholesale adoption of a single model for all situations without appropriate parameter optimisation may not be apt since the characteristics of each Basin are unique and subject to temporal vagaries. In the same context, Tables 7-10 as well as Figure 7, show the relative errors for the different models during the calibration and validation
![]() (a)
(a)![]() (b)
(b)
Figure 7. Simulated flow patterns for (a) Zungeru and (b) Agaie Station during the validation phase.
![]()
Table 6. Reliability and Streamflow variability.
![]()
Table 7. Mean square relative errors (ER) in the calibration phase for logarithmic and exponential models.
![]()
Table 8. Comparison of Root Mean Square Relative errors (ER) during verification for the logarithmic and exponential models.
![]()
Table 9. Model forecast performance of extreme flow value for calibration stations.
![]()
Table 10. Model forecast performance in the validation phase.
phases in terms of correlation metrics. It can be seen that the exponential model using FDC parameter gives reasonably well estimations of the FDC for the stations considered. However, in view of the short length of data used for the study, the model that gives the smallest root mean square relative error (ER) value can be used to predict flow at the ungauged site within the Sub-basins. The contrasts between these values (ER and R2) should not be related since ER is used to measure the prediction error of the proposed models whereas the values of R2 indicate how strong linear correlation existed between the model coefficients (i.e., a1, a2, e1, e2, f1, f2, j1, j2) and the drainage area (A).
Despite the extent of correlation or relative error margins, it is pertinent to point that using just a representative catchment characteristic may not be sufficient to reflect the hydrologic variation of a particular catchment as evidenced in Figure 7(a) where the model under predicted the entire flow regime even though it replicated the flow pattern. The high variability in the flow dynamics probably requires that the obvious need for the employment of catchment characteristics like slope and geology along with the drainage area parameter. This becomes essential especially considering how much overland flow vis-à-vis its time of concentration and the corresponding flow accumulation in streams/rivers and accretions are largely tied to catchment characteristics. In addition, using literally a threshold of 50% significant level of Rmax and Rmin [10] for high and low flows, respectively, the regionalised models performed averagely well in the calibration phase and under predicted both low and high flows in the validation stage, especially the logarithmic model. The only plausible explanation for this abysmal performance of the models could be due to insufficient data length; this does not allow for effective capturing of the relevant flow attributes.
4. Conclusion
Based on the findings of the study it is imperative to note that the regionalisation of flow duration curves is an effective approach for stream flow generation and extension, especially in the face of data scarcity. In addition, it is clearly evident that the use of catchment characteristics as input parameters, to a large extent for model development whether conceptual or statistical model in essential. However, results obtained by employing only the drainage area in the overall regionalised model indicate that it is not representative enough thus considering the length of data used and the attendant problem of flow variability, it suffices to note that an ensemble of catchment characteristics may be imperative. It is also important to take into consideration the ability of the models to reproduce the flow signatures; in this case, the prediction of extreme values is critical. Both the logarithmic and exponential function models employed in the FDCs portrayed different characteristics in the calibration and validation stages. The exponentially regionalised models overwhelmingly performed better than the logarithmic as shown in the validation phase. Considering the results obtained in the overall, objective generalisations may not be possible though, the parameters obtained for the models in the regionalisation procedure were largely optimised. Hence, effective conclusion on the suitability of using the drainage area as a representative parameter in a copious attempt to understand the overall behaviour of a hydrologic response unit should be done with cautious optimism; especially taking cognisance of the implications of geologic characteristics of drainage basins in affecting low flows.
NOTES
![]()
*Corresponding author.