Application of Improved RSM in the Optimization of Automotive Frontal Crashworthiness ()
Received 25 March 2016; accepted 25 April 2016; published 28 April 2016

1. Introduction
Automobile has been used as an indispensable means of transport more and more common in the family, bringing convenience for people, at the same time a large number of traffic accidents have become a serious social problem. The automobile traffic accident methods are as follows: frontal collision, side collision, rear-end collision and rolling etc. According to the statistics of automobile accident statistics, the proportion of different forms of frontal crash accounts for about 40% of all the collision accidents [1] .
In the process of automobile design, the use of the finite element has a great help. According to the results of the finite element analysis, we can know that the application of improved response surface method obtains the optimal thickness value of each component. Through the recalculation of the model, the simulation results are obtained, and the results are compared with that before optimization.
2. Experimental Design and RSM
2.1. Latin Hypercube Design
Latin hypercube sampling method can be used to conduct a comprehensive sampling distribution, and then from the range of values of each layer. The sampling method is a type of design of experiment and widely used in the simulation experiment, often in a large design space, relatively evenly fill test interval, and all the factors containing the same number of partitions [2] . So through all levels of random combination together, every factors at each level can be studied again, fewer samples can reflect test space characteristics, effective sample reduction, improve work efficiency.
2.2. Traditional RSM
No matter what kind of function relationship between variables and objectives in practical engineering problems, the polynomial model can always be used. In the nonlinear design space, the function relation between the design variables x and the response y can be expressed:
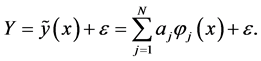 (2-1)
(2-1)
In the equations,  is a target or constraint of approximate function;
is a target or constraint of approximate function;  is a fitting error, and include contain random errors and modeling errors, it obeys the normal distribution
is a fitting error, and include contain random errors and modeling errors, it obeys the normal distribution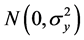 ;
; 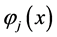 is basis function; N is the base function items;
is basis function; N is the base function items;  is undetermined polynomial regression coefficient vector;
is undetermined polynomial regression coefficient vector;
Each design point is composed of n independent variable, and the quadratic model can be constructed with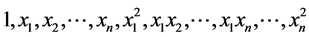 , the approximate function Y of the approximation to the real response is:
, the approximate function Y of the approximation to the real response is:
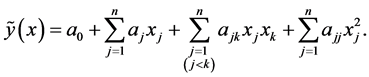 (2-2)
(2-2)
 design of sample points were choiced in the design space, the sample points of finite element were analysised and post proced, the response value vector can be calculated, the coefficient can be determined by least squares method in the Formula (2-2).
design of sample points were choiced in the design space, the sample points of finite element were analysised and post proced, the response value vector can be calculated, the coefficient can be determined by least squares method in the Formula (2-2).
At the sample point , the absolute error of the finite element analysis and the response surface approximation function can be expressed as:
, the absolute error of the finite element analysis and the response surface approximation function can be expressed as:
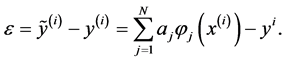 (2-3)
(2-3)
The square sum of the error at the selected 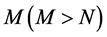 sample points is:
sample points is:
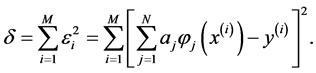 (2-4)
(2-4)
By using the least square method to make error sum of squaresin type (2-4) is the smallest, only need to:
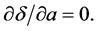 (2-5)
(2-5)
Can obtained polynomial coefficients a:
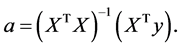 (2-6)
(2-6)
Type (2-6), ![]() is corresponding amount of finite element analysis; the matrix X is composed of
is corresponding amount of finite element analysis; the matrix X is composed of ![]() design point of the basis function, the expression is:
design point of the basis function, the expression is:
![]() (2-7)
(2-7)
2.3. Improved RSM
In the response surface model is the most widely used quadratic polynomial model, reduce the structure calculation, ignoring the cross terms [3] , the expression is:
![]() (2-8)
(2-8)
Type (2-8): ![]() is undetermined factor; P is test vectors.
is undetermined factor; P is test vectors.
The current experimental sites are![]() ,
, ![]() , so:
, so:
![]() (2-9)
(2-9)
![]() (2-10)
(2-10)
Using least square method, according to the type (2-5) get the unbiased estimation of (2-10): ![]() , among them:
, among them:
![]() ;
;![]() ;
;
![]() .
.
Let a plug in type (2-9), ![]() can be obtained, thus the response surface calculation formula is determined.
can be obtained, thus the response surface calculation formula is determined.
2.4. The RSM Error Evaluation
The corresponding surface model accuracy can be tested by the following two aspects:
1) Response surface sample points fitting state decision coefficient ![]() and adjustment coefficient
and adjustment coefficient ![]() can be used to verify, the expression is as follows:
can be used to verify, the expression is as follows:
![]() (2-11)
(2-11)
![]() (2-12)
(2-12)
Among them, p is the number of sample points, k is degrees of freedom, the values is the adjust parameter minus 1, ![]() is response quantities measured values,
is response quantities measured values, ![]() is in response to volume forecast,
is in response to volume forecast, ![]() is the average response of measured values [4] . In the response surface modle, the values of
is the average response of measured values [4] . In the response surface modle, the values of ![]() and
and ![]() closer 1, the more accurate fitting precision.
closer 1, the more accurate fitting precision.
2) In the design space, randomly generated a certain amount of test sample points, to examine its relative error, the relative error expression is as follows:
![]() (2-13)
(2-13)
Type (2-13), y and ![]() respectively measured values and predicted response surface.
respectively measured values and predicted response surface.
3. Based on the Improved RSM for Positive Impact to Optimize the Design of Cars
3.1. The Collision Finite Element Model
Eventually the final vehicle grid is divided as shown in Figure 1. The vehicle is composed of 1,118,522 units, the total number of nodes is 1,115,444. The entire model is composed of 759 parts, the quality is 1257 kg.
3.2. B Pillar Bottom Acceleration Curve Analysis
The acceleration curve of the vehicle B column is shown in Figure 2, the red curve is the right side of B pillar
![]()
Figure 2. Acceleration curve of car B pillar during crash.
deceleration curve, the black curve is the left side of B pillar deceleration curve, it can be seen from two acceleration curve that the maximum acceleration of right B-pillar is 39.9 g and left is 37.2 g. The maximum acceleration is slightly larger, it needs further optimization studies.
3.3. The Optimization Variables Selection and the Model Establishment
This paper is optimized according to the large acceleration of vehicle front crash simulation. Thicknesses of the front and middle parts directly influence the result of the collision, so set the thickness values of front and middle vehicle components as optimization variables, the right B-pillar acceleration peak value as the optimization objective function. Eight parts were selected to the result of larger impact, respectively floor, the front bumper beam, engine compartment outside cover panel, engine compartment inner cover plate, front rails, front panel, fender, front wheel cover plate, the location as shown in Figure 3.
The thickness of each component is ![]() mm, and the corresponding peak acceleration of the right B pillar is
mm, and the corresponding peak acceleration of the right B pillar is![]() . By using the Latin hypercube test method, the
. By using the Latin hypercube test method, the
fitting expression for the acceleration peak value of each component of the design variables and the target value is obtained by the analysis of 17 sample points and the improved response surface method:
![]() (3-1)
(3-1)
The extrapolation accuracy was tested in the nonlinear test sample points by improved response surface model, the 17 sample points of relative error formula applied 2 - 6 calculation. As shown in Figure 4, the improved response surface model has high precision at the 17 sample points.
3.4. The Front Collision Optimization Design
The thicknesses of front and middle parts affect the structure crashworthiness and the B pillar peak acceleration directly [5] . With the right side of B pillar peak acceleration as the optimization goal and eight thicknesses as the design variables, the optimization model is as follows:
![]() (3-2)
(3-2)
Type (3-2):![]() , as the design variable vector;
, as the design variable vector;![]() , as the design variable threshold value vector, its value reduces 15% for the current;
, as the design variable threshold value vector, its value reduces 15% for the current;![]() , as the design variable upper limit value vector, its value increases 15% for the current.
, as the design variable upper limit value vector, its value increases 15% for the current.
The optimization variable is obtained using sequential quadratic programming algorithm, as follows: ![]() mm. Based on the consideration of the manufacturing process, the thickness of steel plate precision is 0.1 mm, so the thicknesses eventually were set to
mm. Based on the consideration of the manufacturing process, the thickness of steel plate precision is 0.1 mm, so the thicknesses eventually were set to ![]() mm.
mm.
The thicknesses of components were changed in Hyper Mesh software, new model was calculated again by LS-DYNA.
3.5. The Optimization Results Analysis
The acceleration curves comparison is shown in Figure 5.
We can know that the right peak acceleration of B pillar is 30.8 g, reduced about 22.8% in Figure 5. The collision performance was obviously improved after optimization, achieved the desired effect.
4. Conclusion
In vehicle crash simulation test, the front and middle vehicle body structure affects crashworthiness directly.
![]()
Figure 3. Design variables for optimization.
![]()
Figure 4. Relative error of improved response surface model.
![]()
Figure 5. Acceleration curve of right B-pillar before and after optimization.
In order to improve the performance of vehicle collision, eight parts were selected which have large impact for the result, its thickness as design variables to the right of the B-pillar acceleration peak of optimization goal; the application of improved response surface method can obtain the optimization thickness value of different parts. The right side of the B pillar acceleration decreased about 22.8%, compared with before optimization; so that the result has reached the expected purpose.