Marginal Conceptual Predictive Statistic for Mixed Model Selection ()
Received 9 March 2016; accepted 23 April 2016; published 26 April 2016

1. Introduction
With the development in data science over the past decades, people become more aware of the complexity of data in real life. Univariate linear regression models with independent identically distributed (i.i.d.) Gaussian errors cannot achieve good fitness for some types of data, especially for the data with observations that are correlated. For instance, in longitudinal data, observations are usually recorded from the same individual over time. It is reasonable to assume that correlation exists among the observations from the same individual and linear mixed models are therefore appropriately utilized for modeling such data.
Since linear mixed models are extensively used, mixed model selection plays an important role in statistical literature. The aim of mixed model selection is to choose the most appropriate model from a candidate pool in the mixed model setting. To facilitate this task, a variety of model selection criteria are employed to implement the selection process.
In linear mixed models, a number of criteria have been developed to characterize model selection. The most widely used criteria are the information criteria such as the AIC [3] [4] and the BIC [5] . Sugiura [6] proposed a marginal AIC (mAIC) which involved the number of random effects parameters into the penalty term. Shang and Cavanagh [7] employed the bootstrap method to estimate the penalty term of mAIC for proposing two variants of AIC. For longitudinal data, a special case of linear mixed models, Azari, Li and Tsai [8] proposed a corrected Akaike Information Criterion (AICc). In the justification of AICc, the paper mainly handled the challenge initiated by the correlation matrix under certain conditions for the mixed models. Vaida and Blanchard [9] redefined the Akaike information based on the best linear unbiased predictor (BLUP) [10] - [12] for the random effects in the mixed models, and proposed a conditional AIC (cAIC). Dimova et al. [13] derived a series of variants of the Akaike Information Criterion in small samples for linear mixed models.
Another information criterion, BIC, can be considered as a Bayesian alternative to AIC. In linear mixed models, BIC is converted from marginal AIC by replacing the constant 2 in the penalty by , where N is the sample size (mBIC) [14] . Jones [15] proposed a measure of the effective sample size to replace the sample size in the penalty term of BIC, leading to a new criterion BICJ.
, where N is the sample size (mBIC) [14] . Jones [15] proposed a measure of the effective sample size to replace the sample size in the penalty term of BIC, leading to a new criterion BICJ.
We note that the BIC-type information criteria are derived using Bayesian approaches. Different from that, the AIC-type information selection criteria are justified from the frequentist perspective and based upon the information discrepancy. However, little research has relied on other discrepancy to propose criteria including Mallows’ Cp [1] [2] in linear mixed models. In fact, because of dissimilar derivation, each selection criterion has its own advantages, and no unique selection criterion can cover all the benefits for model selection. To further develop the selection criteria in the mixed modeling setting, we aim to justify the Cp-type ones relying on the Gauss discrepancy.
Mallows’ Cp [1] [2] in linear regression models targets to estimate the Gauss discrepancy between the true model and a candidate model. It serves as an asymptotically unbiased estimator of the expected Gauss discrepancy. Fujikoshi and Satoh [16] identified Cp in multivariate linear regression. Davies et al. [17] presented the estimation optimality of Cp in linear regression models. Cavanaugh et al. [18] provided an alternate version of Cp. The Gauss discrepancy is an L2 norm measuring the distance between the true model and a candidate model in linear models. To select the most appropriate model among competing fitted models, the candidate model leading to the smallest value of Cp is chosen. However, since the covariance matrix of linear mixed models poses the challenge for the justification of selection criteria, Cp statistic in linear mixed models has not been identified.
This paper extends the justification of Cp from linear models to linear mixed models. We first define a marginal Gauss discrepancy reflecting the correlation for measuring the distance between the true model and a candidate model. We utilize the assumption that under certain conditions, the estimator of the correlation matrix for the candidate model is consistent to that for the true correlation matrix. The marginal Cp, abbreviated as MCp. MCp serves as an asymptotically unbiased estimator of the expected marginal Gauss discrepancy between the true model and a candidate model. An improvement of MCp, abbreviated as IMCp, is also proposed and proved. We then justify IMCp as an asymptotically more precisely unbiased estimator of the expected marginal Gauss discrepancy. We examine the performance of the proposed criteria in a simulation study where we utilize various correlation structures and different sample sizes.
The paper is organized as follows: Section 2 presents the notation and defines the marginal Gauss discrepancy in the setting of linear mixed models. In Section 3, we provide the derivations of the model selection criteria MCp and IMCp. Section 4 presents a simulation study to demonstrate the effectiveness of the proposed criteria. Section 5 concludes.
2. Marginal Gauss Discrepancy
In this section, we will introduce the true model, also called the generating model, and the candidate model in the setting of linear mixed models, then define the marginal Gauss discrepancy.
Suppose that the generating model for the data is given by
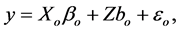 (2.1)
(2.1)
where y denotes an N × 1 response vector, Xo is an N × po design matrix of full column rank, βo is a po × 1 unknown vector for fixed effects. Z is an N × mr known matrix of full column rank and bo is an mr × 1 unknown vector for random effects, where m is the number of cases, the sample size, and r is the dimension of the random effects for each case. Here, 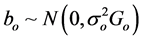 ,
, 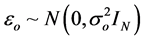 , and bo and εo are mutually independent and Go is a positive definite matrix and
, and bo and εo are mutually independent and Go is a positive definite matrix and 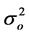 is a scalar.
is a scalar.
We fit the data with a candidate model of the form
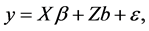 (2.2)
(2.2)
where X is an N × p design matrix of full column rank, β is a p × 1 unknown vector,  ,
,  , and b and ε are mutually independent. The design matrix of the random effects Z and the random effects b are the same as those in the generating model. The matrix G is a positive definite matrix with the q unknown parameters in it.
, and b and ε are mutually independent. The design matrix of the random effects Z and the random effects b are the same as those in the generating model. The matrix G is a positive definite matrix with the q unknown parameters in it.
Since the random part of the model (i.e. Zb) is not subject to selection, it is easier to use the marginal form in [19] of linear mixed models. Let , then the generating model (2.1) can be written as
, then the generating model (2.1) can be written as
 (2.3)
(2.3)
where the scaled variance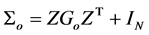 .
.
For the candidate model (2.2), let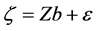 , we have
, we have
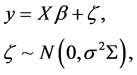 (2.4)
(2.4)
where the scaled variance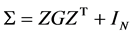 . Therefore, the Σ is a nonsingular positive definite matrix.
. Therefore, the Σ is a nonsingular positive definite matrix.
In models (2.3) and (2.4), the terms ζo and ζ are the combinations of the random effects and errors in the model, respectively. Since they are both assumed to have mean zero, the parameters scaled variances Σo and Σ contain all the information of the random effects and errors, including the correlation structures.
We measure the distance between the true model and a candidate model by defining the marginal Gauss discrepancy based on the marginal forms of models (2.3) and (2.4). The true model is assumed to be included in the pool of candidate models. Let θo and θ denote the vectors of parameters 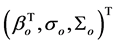 and
and![]() , respectively. The marginal Gauss discrepancy between the true model and a candidate model is defined as
, respectively. The marginal Gauss discrepancy between the true model and a candidate model is defined as
![]()
where Eo denotes the expectation with respect to the true model. Note that the marginal Gauss discrepancy contains a weight of inverse scaled variance Σ−1 into the L2 norm. Therefore, the correlation between observations is involved when we use the marginal Gauss discrepancy to measure the distance between the true model and a candidate model.
Now let ![]() denote an estimate of θ. For instance,
denote an estimate of θ. For instance, ![]() could be the maximum likelihood estimator (MLE) or the restricted maximum likelihood estimator (REML). However, in this paper, the MLE is utilized. The marginal Gauss discrepancy between the true model and the fitted candidate model is defined as
could be the maximum likelihood estimator (MLE) or the restricted maximum likelihood estimator (REML). However, in this paper, the MLE is utilized. The marginal Gauss discrepancy between the true model and the fitted candidate model is defined as
![]()
which can be therefore expressed as
![]() (2.5)
(2.5)
We define a transformed marginal Gauss discrepancy between the true generating model and the fitted candidate model as a linear function of the marginal Gauss discrepancy (2.5) as
![]() (2.6)
(2.6)
Taking the expectation of the transformed marginal Gauss discrepancy (2.6), we obtain the expected transformed marginal Gauss discrepancy as
![]() (2.7)
(2.7)
To serve as a model selection criterion based on the expected transformed marginal Gauss discrepancy in Equation (2.7), an unbiased estimator or an asymptotically unbiased estimator will be proposed. To simplifying the procedure, we will first abbreviate this discrepancy in Equation (2.7).
From expression (2.7), the expectation part in the numerator can be written as
![]() (2.8)
(2.8)
where ![]() is a projection matrix such that
is a projection matrix such that![]() . To explore a further expression of (2.8), we need to know the properties of
. To explore a further expression of (2.8), we need to know the properties of![]() .
.
Theorem 1. For every![]() , the matrix
, the matrix ![]() satisfies the following properties:
satisfies the following properties:
1) ![]() is idempotent.
is idempotent.
2) ![]() and
and![]() .
.
The proof is given in the Appendix.
Corollary 1. Following Theorem 1, we have:
1)![]() .
.
2)![]() .
.
3)![]() .
.
The proof of Corollary 1 can be easily completed following Theorem 1.
By Corollary 1, expression (2.8) can be written as
![]() (2.9)
(2.9)
Note that the scaled variance Σ is a function of the q unknown parameter vector of variance components γ, i.e.,![]() . Azari, Li and Tsai [8] noted that under the assumption that the set of candidate models includes the true model, it is reasonable to assume that the MLE
. Azari, Li and Tsai [8] noted that under the assumption that the set of candidate models includes the true model, it is reasonable to assume that the MLE ![]() is a consistent estimator of
is a consistent estimator of![]() . Therefore, we can approximate
. Therefore, we can approximate ![]() by Σ, i.e.,
by Σ, i.e.,![]() . In what follows, we will make use of this approximation.
. In what follows, we will make use of this approximation.
First, since ![]() and
and![]() , using the approximation
, using the approximation ![]() and Theorem 1, we have the first term of (2.9) as
and Theorem 1, we have the first term of (2.9) as
![]() (2.10)
(2.10)
Second, using the approximation ![]() again, the first term of Equation (2.7) can be simplified as
again, the first term of Equation (2.7) can be simplified as
![]() (2.11)
(2.11)
Using expressions (2.9), (2.10), and (2.11), ![]() in (2.7) can be therefore approximated as
in (2.7) can be therefore approximated as
![]() (2.12)
(2.12)
Following Mallows’ interpretation, ![]() in (2.12) can be expressed as
in (2.12) can be expressed as
![]()
where VP and Bp are respectively “variance” and “bias” contributions given by
![]()
and
![]()
We comment that increasing the number of the parameters of the fixed effects p will decrease the bias Bp for the fitted model, yet will increase the variance VP at the same time. The marginal Gauss discrepancy can therefore be considered as a bias-variance trade-off. Since a smaller value of the discrepancy indicates a smaller distance between the true model and a candidate model, the size of the Gauss discrepancy can really reflect how a fitted model is close to the true model.
3. Derivations of Marginal Cp and Improved Marginal Cp
3.1. Marginal Cp
In this section, model selection criteria based on ![]() are developed by finding a statistic that has an expectation which equals to or asymptotically equals to the expected transformed marginal Gauss discrepancy.
are developed by finding a statistic that has an expectation which equals to or asymptotically equals to the expected transformed marginal Gauss discrepancy.
We start with the expectation of the sum of squared errors SSRes from a candidate model. In linear mixed models, the sum of squared errors SSRes can be written as
![]()
By Theorem 1 and Corollary 1, the expectation of the “scaled sum of squared error” ![]() can be expressed by
can be expressed by
![]()
and then we have
![]() (3.1)
(3.1)
Similar to the derivation of Equation (2.11), the numerator of first term of Equation (3.1) is expressed as
![]() (3.2)
(3.2)
Then, by Equations (3.1) and (3.2), it is straightforward to construct a function![]() , which is a linear combination of
, which is a linear combination of![]() . It can be shown that the function T has the expectation
. It can be shown that the function T has the expectation
![]()
Note that the function T is not a statistic since the parameter ![]() is unknown. Here, we would like to use an estimator
is unknown. Here, we would like to use an estimator ![]() to replace
to replace ![]() in the function. Let
in the function. Let ![]() denote the design matrix for the largest model in the candidate pool with
denote the design matrix for the largest model in the candidate pool with![]() . We assume that
. We assume that![]() . Let
. Let ![]() represent the sum of squared errors for the corresponding fitted model and is written as
represent the sum of squared errors for the corresponding fitted model and is written as
![]()
where ![]() and
and ![]() are the MLEs for parameters
are the MLEs for parameters ![]() and
and ![]() in the largest candidate model respectively. The estimator
in the largest candidate model respectively. The estimator ![]() cannot be expressed in a closed form and is calculated by computational algorithm where the iterations are needed.
cannot be expressed in a closed form and is calculated by computational algorithm where the iterations are needed.
For the estimator of![]() , we use the mean squared error of the largest candidate model
, we use the mean squared error of the largest candidate model
![]() (3.3)
(3.3)
which is an asymptotically unbiased estimator for![]() , yet it is biased. In the justification of this estimator, using the approximation
, yet it is biased. In the justification of this estimator, using the approximation![]() , we can represent
, we can represent ![]() in terms of
in terms of![]() , then the expected value of
, then the expected value of ![]() can be easily calculated as
can be easily calculated as![]() , i.e., asymptotically we can have
, i.e., asymptotically we can have![]() . Serving as an asymptotically unbiased estimator of
. Serving as an asymptotically unbiased estimator of![]() , the
, the ![]() in Equation (3.3) for the largest candidate model is preferred to estimate
in Equation (3.3) for the largest candidate model is preferred to estimate![]() .
.
MCp is then obtained as
![]() (3.4)
(3.4)
Note that MCp is biased for![]() . However, under the assumption that the true model is included in the pool of candidate models, MCp serves as an asymptotically unbiased estimator of the discrepancy in expression (2.7). The proof is nontrivial, yet the simulations (not presented here) can show that as the samples size increases, the curves of the average values for MCp and the discrepancy
. However, under the assumption that the true model is included in the pool of candidate models, MCp serves as an asymptotically unbiased estimator of the discrepancy in expression (2.7). The proof is nontrivial, yet the simulations (not presented here) can show that as the samples size increases, the curves of the average values for MCp and the discrepancy![]() , along with IMCp, which will be introduced in the following subsection, collectively get merged, indicating that MCp and IMCp are all asymptotically unbiased estimators of the discrepancy
, along with IMCp, which will be introduced in the following subsection, collectively get merged, indicating that MCp and IMCp are all asymptotically unbiased estimators of the discrepancy![]() .
.
3.2. Improved Marginal Cp
To improve the performance of the MCp statistic in linear mixed models, we wish to propose an improved marginal Cp, called IMCp, which is expected to be a more accurate or less biased estimator of the expected transformed marginal Gauss discrepancy than MCp. IMCp is proposed as
![]() (3.5)
(3.5)
where SSRes and ![]() are the sum of squared errors from the candidate fitted model and the largest fitted model, respectively. Note that IMCp provides us an asymptotically unbiased estimator of
are the sum of squared errors from the candidate fitted model and the largest fitted model, respectively. Note that IMCp provides us an asymptotically unbiased estimator of![]() , i.e.,
, i.e., ![]() , and it will be shown in what follows.
, and it will be shown in what follows.
To evaluate the expectation of IMCp, we first need to calculate the ratio of the sum of squared errors ![]() between the candidate model and the largest candidate model in the pool. By Corollary 1, we have
between the candidate model and the largest candidate model in the pool. By Corollary 1, we have
![]()
By using the approximation ![]() for all
for all![]() , we approximate
, we approximate ![]() and
and ![]() by H and
by H and![]() , respec-
, respec-
tively, and ![]() and
and![]() . Then, the ratio
. Then, the ratio ![]() can be written as
can be written as
![]() (3.6)
(3.6)
To continue the proof, we will use the following theorem and corollary.
Theorem 2. If![]() , then for any
, then for any ![]() matrix K, we have
matrix K, we have![]() .
.
The proof of Theorem 2 is presented in the Appendix.
Corollary 2. Following Theorem 2, we can obtain following results:
1)![]() .
.
2)![]() .
.
The proof of Corollary 2 is included in the Appendix.
By Theorem 1 and Corollary 2, we have
![]()
such that the quadratic forms ![]() and
and ![]() are independent. It follows that the
are independent. It follows that the
expectation of ![]() in (3.6) can be written as
in (3.6) can be written as
![]() (3.7)
(3.7)
For the term ![]() in (3.7), since
in (3.7), since![]() , we have
, we have
![]() (3.8)
(3.8)
For the term ![]() in (3.7), we can prove that
in (3.7), we can prove that
![]()
Note that![]() . To justify the distribution of
. To justify the distribution of![]() , we have
, we have
![]()
where![]() . For the distribution of y, we know that
. For the distribution of y, we know that![]() . We calculate that
. We calculate that![]() , and by Theorem 1, the matrix
, and by Theorem 1, the matrix ![]() is idempotent. Therefore, we have
is idempotent. Therefore, we have![]() , where
, where
![]() and by Corollary 2, we can calculate λ as
and by Corollary 2, we can calculate λ as
![]()
Now, its inverse ![]() follows an inverse Chi-square distribution, i.e.,
follows an inverse Chi-square distribution, i.e., ![]() , with the expectation as
, with the expectation as
![]() (3.9)
(3.9)
Using the results of (3.8) and (3.9), we have the expectation of ![]() in (3.7) as
in (3.7) as
![]() (3.10)
(3.10)
We recall that the criterion IMCp in (3.5) is defined as
![]()
By the result of (3.10) and the approximation ![]() again , we have the expectation of IMCp as
again , we have the expectation of IMCp as
![]()
Hence, IMCp is an asymptotically unbiased estimator of the expected overall transformed Gauss discrepancy ![]() in Equation (2.7). The advantage of IMCp is that it avoids the bias of using
in Equation (2.7). The advantage of IMCp is that it avoids the bias of using ![]() to estimate
to estimate ![]() to derive the criterion comparing to the derivation of MCp.
to derive the criterion comparing to the derivation of MCp.
We comment that the proposed MCp and IMCp are justified based upon the assumption that the true model is contained in the candidate models. Hence, we can calculate the MCp and IMCp values for the correctly and overfitted candidate models. However, the proposed criteria are also can be utilized for the underspecified models except that the values will be quite large and not behave well.
4. Simulation Study
In this simulation study, we investigate the ability of MCp in (3.4) and IMCp in (3.5) to determine the correct set of fixed effects for the simulated data in different models.
4.1. Presentation of Simulations
Consider a setting in which data are generated by the model of the following form
![]()
where the random effects ![]() are uncorrelated with mean 0 and variance
are uncorrelated with mean 0 and variance![]() , the errors
, the errors ![]() are independent with each other with mean 0 and variance
are independent with each other with mean 0 and variance![]() . It follows that the correlation between any two observa-
. It follows that the correlation between any two observa-
tions from the same case is![]() , whereas the observations from different cases are uncorrelated. Let f denote the proportion between the variance of the random effects and the variance of the errors, i.e.
, whereas the observations from different cases are uncorrelated. Let f denote the proportion between the variance of the random effects and the variance of the errors, i.e.![]() . We can obtain that the correlation between the observations from the same case equals
. We can obtain that the correlation between the observations from the same case equals![]() , which is an increas-
, which is an increas-
ing function of f. Therefore, a higher f implies a higher correlation between the observations in the same case.
For convenience, the generating model can also be expressed by
![]()
where ![]() are unknown coefficients of the fixed effects. It is assumed that the random effects
are unknown coefficients of the fixed effects. It is assumed that the random effects ![]() with
with![]() , and
, and![]() . We set
. We set ![]() for
for![]() , an ni-vector of ones, and
, an ni-vector of ones, and ![]() . We also assume that the error term
. We also assume that the error term![]() , and is independent of the random effects b.
, and is independent of the random effects b.
Since the random part of the model (i.e. Zb) is not subject to selection, we would like to express the model by its marginal form. Let![]() , we have
, we have
![]()
which can also be expressed by the general form as
![]() (4.1)
(4.1)
where![]() ,
, ![]() is a scaled covariance matrix. Equivalently, the term
is a scaled covariance matrix. Equivalently, the term ![]() has the following exchangeable correlation structure:
has the following exchangeable correlation structure:![]() , where
, where![]() , I is the identity matrix and J is the matrix of 1’s.
, I is the identity matrix and J is the matrix of 1’s.
In this simulation study, we generate the design matrix X with ![]() of 5. The first column of X is 1 and the other four columns of X are generated randomly from uniform distributions but are fixed throughout the simulations. Therefore, the number of fixed effects including the intercept in the largest model is
of 5. The first column of X is 1 and the other four columns of X are generated randomly from uniform distributions but are fixed throughout the simulations. Therefore, the number of fixed effects including the intercept in the largest model is![]() . We assume that the candidate vectors of covariates,
. We assume that the candidate vectors of covariates, ![]() from which the columns of X are to be selected, then there are
from which the columns of X are to be selected, then there are ![]() candidate models in the candidate pool. Here, we will illustrate the behavior of model selection criteria by choosing three generating models:
candidate models in the candidate pool. Here, we will illustrate the behavior of model selection criteria by choosing three generating models:
1) Model 1:![]() ,
,![]() ;
;
2) Model 2:![]() ,
,![]() ;
;
3) Model 3:![]() ,
,![]() .
.
These three models correspond to the three bs:![]() ,
, ![]() and
and ![]() in model (4.1) with the number of fixed effects
in model (4.1) with the number of fixed effects ![]() equals 2, 3, 4, respectively. Again, the MLEs are used for estimation in the simulations.
equals 2, 3, 4, respectively. Again, the MLEs are used for estimation in the simulations.
Furthermore, we consider the case where the correlated errors have varying degrees of exchangeable structure. The variance component of error term ![]() is taken to be 1, and four values in an increasing order of
is taken to be 1, and four values in an increasing order of ![]() are considered: 3, 6, 9, corresponding to three values of f: 3, 6, 9, respectively. We take the number of clusters (m) to be 5, 10 and 20, the number of repetitions in a cluster to be fixed at n = 5. We employ a total of 100 realizations for each model.
are considered: 3, 6, 9, corresponding to three values of f: 3, 6, 9, respectively. We take the number of clusters (m) to be 5, 10 and 20, the number of repetitions in a cluster to be fixed at n = 5. We employ a total of 100 realizations for each model.
4.2. Results
4.2.1. Model 1: ![]()
Table 1 presents the performance of the two versions of marginal Cp (MCp and IMCp), mAIC and mBIC, under model 1 with the true fixed effects parameter![]() , and corresponding to po = 2. The correct model selection rate for each criterion is listed. We observe that corresponding to each f, the IMCp outperforms the MCp, and both outperform mAIC and mBIC in selecting the correct model for small samples. With the increasing of the ratio f, we can observe the better performance in selecting the correct model from our proposed criteria.
, and corresponding to po = 2. The correct model selection rate for each criterion is listed. We observe that corresponding to each f, the IMCp outperforms the MCp, and both outperform mAIC and mBIC in selecting the correct model for small samples. With the increasing of the ratio f, we can observe the better performance in selecting the correct model from our proposed criteria.
4.2.2. Model 2: ![]()
We evaluate the proposed criteria for model 2 in the same manner as for model 1. Table 2 presents the performance of MCp and IMCp, mAIC and mBIC under model 2, where the true fixed effects parameter is ![]() and po = 3. The only change on model 2 from model 1 is that we add one more fixed effect variable X5 and set the coefficient of that variable
and po = 3. The only change on model 2 from model 1 is that we add one more fixed effect variable X5 and set the coefficient of that variable![]() . In Table 2, the simulation results of model 2 are similar to those of model 1. With the increasing of the ratio f, we can have the better performance from our proposed criteria MCp and IMCp, indicating that the proposed MCp and IMCp can effectively fulfill the mission of model selection in the mixed models. We can also observe and conclude that IMCp has improved the performance of MCp for model selection in small samples. With the increasing of m, the performance of IMCp and MCp becomes closer. Comparing to the correct selection rates in model 1, all model selection criteria behave better in model 2.
. In Table 2, the simulation results of model 2 are similar to those of model 1. With the increasing of the ratio f, we can have the better performance from our proposed criteria MCp and IMCp, indicating that the proposed MCp and IMCp can effectively fulfill the mission of model selection in the mixed models. We can also observe and conclude that IMCp has improved the performance of MCp for model selection in small samples. With the increasing of m, the performance of IMCp and MCp becomes closer. Comparing to the correct selection rates in model 1, all model selection criteria behave better in model 2.
4.2.3. Model 3: ![]()
As in the first two models, we evaluate the performance of model selection criteria by the rates in correctly selecting the true model. The results are presented in Table 3. Model 3 is identical to model 2 with the exception that we add one more significant fixed effect variable X2 with the coefficient![]() .
.
The simulation results of model 3 are similar to those of models 1 - 2. Considering the rates in choosing the correct model, we can find the trend of dramatic improvement of all criteria on model 3 over those on models 1 and 2, implying that the proposed MCp and IMCp essentially and effectively implement model selection when the fixed-effects are significant. In moderately large (m = 20) sample sizes, compared to that of mAIC and mBIC, MCp and IMCp have comparative performance in selecting the correct model.
![]()
Table 1. Correct selection rate in model 1.
![]()
Table 2. Correct selection rate in model 2.
![]()
Table 3. Correct selection rate in model 3.
5. Concluding Remarks
The simulation results illustrate that the proposed criteria MCp and IMCp outperform mAIC and mBIC when the observations are highly correlated in small samples. The results also show that with the increasing of the ratio f between the variance for the random effects and that for errors, the MCp and IMCp perform better. Since a larger f implies a higher correlation between the observations, we can conclude that with the correlation between observations increases, a better performance from the proposed criteria MCp and IMCp would be observed. Since the model with a small f which close to 0 is similar to a linear regression model with independent errors, our proposed criteria are not advantageous to be applied in such case.
The simulation results show that the proposed criteria MCp and IMCp significantly outperform mAIC and mBIC when the sample size is small. As the sample size increases, the performance of the proposed criteria becomes comparable to that of mAIC and mBIC. Therefore, MCp and IMCp are highly recommended in small samples in the setting of linear mixed models.
Our research (not shown in this paper) also shows that both proposed criteria behave best when the maximum likelihood estimation (MLE) is employed, comparing to those when the restricted maximum likelihood estimation or least squares estimation are used. The research on MCp and IMCp under REML estimation needs to be further developed in the future.
In the simulation study, by the comparison among models 1, 2 and 3, we see that when the true model includes more significant fixed effect covariates, the proposed criteria perform better in selecting the correct model. This fact indicates that the models with more significant variables (larger bs) are more identifiable by the proposed criteria than the models with variables which are not quite significant.
Comparing the performance between MCp and IMCp, we find that when the sample size is small, IMCp obtains a higher correct selection rate than MCp, which demonstrates that IMCp improves the performance of MCp in selecting the most appropriate model. However, when the sample size becomes larger, the performance of MCp and IMCp is quite identical.
Regarding the consistency of a model selection criterion, it means that as the sample size increases, the model selection will select the true model with probability 1. Note that MCp, IMCp, and mAIC are not consistent, whereas mBIC is consistent as expected since its penalty term ![]() prevents the overfitting in large samples. As the simulation study demonstrates, we can address again that the proposed criteria MCp and IMCp validate their advantages in small samples, although they are originally justified with large sample approximations, which is similar to quite a few other model selection criteria. The details for the consistency of model selection criteria in linear mixed models can also see Jiang and Rao [20] .
prevents the overfitting in large samples. As the simulation study demonstrates, we can address again that the proposed criteria MCp and IMCp validate their advantages in small samples, although they are originally justified with large sample approximations, which is similar to quite a few other model selection criteria. The details for the consistency of model selection criteria in linear mixed models can also see Jiang and Rao [20] .
Appendix
Proof of Theorem 1. 1) To prove that ![]() is idempotent, we calculate
is idempotent, we calculate
![]()
Thus, we prove that ![]() is idempotent.
is idempotent.
2) By the properties of trace, we have
![]()
Therefore, we have
![]()
Thus, Theorem 1 is proved. □
Proof of Theorem 2. Let![]() . We need to show that
. We need to show that![]() .
.
Since![]() , there exists a p × 1 vector β1 such that
, there exists a p × 1 vector β1 such that![]() .
.
By![]() , there also exists a p × 1 vector β2 such that
, there also exists a p × 1 vector β2 such that![]() , which makes
, which makes ![]() .
.
So we have![]() . □
. □
Proof of Corollary 2. 1) Since ![]() is positive definite, there exists an N × N matrix V with
is positive definite, there exists an N × N matrix V with![]() ,
,
such that![]() . It follows that
. It follows that![]() .
.
Let![]() , we can have
, we can have![]() . Then, we arrive at
. Then, we arrive at
![]()
Now, let
![]()
and
![]()
Since![]() , by Theorem 2, we have
, by Theorem 2, we have![]() , so that we can have
, so that we can have![]() , which leads to
, which leads to
![]()
The first part of Corollary 2 is therefore proved.
2) Following the first part proof of Corollary 2, since![]() , we have
, we have![]() . Then, we can conclude that
. Then, we can conclude that
![]()
Therefore, the proof for the second part of Corollary 2 is completed. □
NOTES
![]()
*Corresponding author.