Mathematical Modeling and Determination of Effective Diffusivity of Mesquite during Convective Drying ()
Received 17 March 2016; accepted 18 April 2016; published 21 April 2016

1. Introduction
Brazil is the country with the greatest potential for research with plant species in the world, because it has the largest and richest biodiversity on the planet distributed in six distinct biomes that have about 55,000 described species [1] . Plant foods are important because of their content of micronutrients, especially vitamins and minerals, but also because of the phytochemical bioactive compounds with antioxidant properties [2] .
Mesquite was introduced in Brazil, especially in the Northeast, due to its hardiness and because it has the important characteristic of fruiting in the driest time of the year when natural fodder stocks reach a critical stage, thus providing a great food nutritional value, especially for feeding caprine and bovine [3] .
The pods of mesquite tree are among the oldest foods used by man in the New World. Fruits of mesquite tree are yellow, long, flat pods and usually slightly curved, palatable, aromatic and sweet; it is in pods that is concentrated nutritional value, being a rich source of carbohydrate. The pod is rich in sugars, proteins, minerals and fiber that can be converted into raw material in production of cakes, breads, cookies, drinks, condiments, jams, honeys, puddings, soups, porridge and other tasty and nutritious food [4] .
Because of all this information, mesquite pods have been a potential source of raw material for the development of a range of products and technological innovations that are being studied by researchers from various countries, like mesquite whole meal, produced in Kenya, Brazil, United States, Argentina and Mexico, and Peruvian algarobina, exported to many countries [5] .
Drying is a method of preservation wherein water content and water activity of fruits, vegetables and grains are diminished through mass and heat transfer phenomena, which minimizes chemical, physical, biochemical and microbiological degradation of these products during storage, ensuring their quality and stability [6] . Drying also allows determining some properties of agricultural products, such as effective diffusivity, describing the water output speed of organic products and it is important for dryers project [7] .
Mathematical representation of drying process of various agricultural products has, for some time, been studied and used in attempting to predict the phenomena that occur during this process [8] . Information relating to the subject is extremely important to assist in the development of equipment and adaptations of existing ones in order to obtain greater efficiency in this key step during post-harvest period.
Considering the importance of theoretical study of drying process for agricultural products and a limitation of information about the phenomena that occur during the drying of mesquite, the objectives of this study were: to study mesquite drying kinetics with an initial water content of 20% (wet basis), in a thin layer, using temperatures of 50˚C, 60˚C, 70˚C and 80˚C and adjusting mathematical models Fick, Page, Cavalcanti-Mata, Henderson & Pabis and Two Exponential Terms to the experimental data and determine the effective diffusion coefficient using flat plate geometry with a sample with 6.5 mm thickness.
2. Materials and Methods
2.1. Location of the Experiments
Experiments were performed in Food Engineering Laboratories of the Federal University of Campina Grande, in the city of Campina Grande, PB.
2.2. Raw Material
For experiments it was used mature mesquite [Prosopis juliflora (Sw.) DC.], obtained in the city of Serra Branca, PB, with initial moisture content of approximately 20% (wb).
2.3. Reception of Raw Material
Mesquite samples were received in nylon bags and transported to the site of the experiments, where they were packed in polyethylene film and stored in a horizontal freezer, temperature −50˚C, in order to preserve its characteristics for the study.
2.4. Cleaning and Cutting
Mesquite cleaning was performed with chlorinated water spray at 30 ppm; then rinsing with potable water at room temperature and subsequent drying (with paper towels), allowing thus eliminate of the surface dirt as: earth, debris and impurities of several species that could affect the quality of the product; subsequently, mesquite was subjected to manual cut in order to standardize product at approximately 20 mm length.
2.5. Drying
Experiments were performed using temperatures of 50˚C, 60˚C, 70˚C and 80˚C, drying air speed of 2 m∙s−1, to constant weight. These parameters were chosen based on the type of raw material, because it is an organic product with sensitive components; as the objective was to preserve maximum nutrients, were not used temperatures above 80˚C; temperatures below 50˚C are not indicated for the study due to very high drying time, thus resulting in high costs and energy consumption.
In drying process was used convective dryer (Figure 1) with fixed bed and upflow air, equipped with an electric heating air system and forced convection. In drying operation was used aluminum baskets measuring 150 mm long and 200 mm wide with 50 g capacity, containing mesquite pods arranged in a single thin layer.
The dryer and the electrical resistances were turned on until the desired temperature for each experiment was obtained; any adjustment of temperatures was performed by a temperature controller and a PT100 probe. It was made, also, measures the speeds of air with the aid of the anemometer, and temperature and relative humidity of air, with the aid of thermo-hygrometer.
To determine the kinetics of drying mesquite, weighing were carried out with product in baskets at predetermined intervals until constant weight; all of the experiments were performed in triplicate; experimental data were expressed as a ratio of water content, calculated by Equation (1). Mathematical models of Fick, Page, Cavalcanti-Mata, Two Exponential Terms, and Henderson & Pabis were used to fit to experimental data and are described in Table 1. These models were chosen because they are the most recommended by some authors
![]()
Figure 1. Convective dryer used in research.
![]()
Table 1. Mathematical models used for drying kinetics.
[9] - [11] to describe drying kinetics of grains and seeds. Coefficients of these equations were obtained by setting the drying curves to the experimental data using the Statistica computer software, version 7.0.
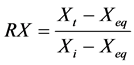 . (1)
. (1)
In which:
RX―ratio of water content, dimensionless;
Xt―water content at time t, dry basis, bs;
Xeq―equilibrium water content, bs;
Xi―initial moisture content, bs.
For calculation of the effective diffusivity (Def) it was used flat plate geometry with a sample with 6.5 mm thick ness, using the Fick model with first term of the series.
For sufficiently long drying times, first term of the series of Fick Equation (n = 0) gives a good estimate solution and Equation (2) can be applied to calculate effective diffusivity.
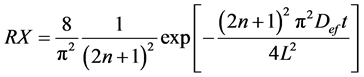 . (2)
. (2)
Linearizing Equation (3.2) and by plotting the graph of ln(RX) versus time, inclination is obtained (K0) according to Equation (3). From the analogy of Page equations, Cavalcanti-Mata and Henderson & Pabis with Fick equation, effective diffusivity was also calculated from Equations (4) and (5) for all drying conditions.
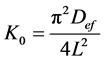 (3)
(3)
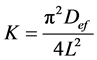 (Page and Henderson & Pabis); (4)
(Page and Henderson & Pabis); (4)
 (Cavalcanti-Mata). (5)
(Cavalcanti-Mata). (5)
As a criterion to determine the model that best represented the experimental data, it was used coefficient of de termination (R2) and the root mean square error (RMSE), described in Equation (6).
 . (6)
. (6)
In which:
RMSE―root mean square error;
RXpred―predicted water content ratio;
RXexp―experimental ratio of water content;
N―number of observations.
2.6. Storage
After drying process, mesquite was packed in flexible film BOPP (biaxially orientated polypropylene) and kept at room temperature of 25˚C ± 3.0˚C.
3. Results and Discussion
Drying kinetics and application of mathematical models can be modified by Dring kinetics.
In Figure 2, curves are obtained by adjusting models of Fick (A), Page (B) Cavalcanti Mata (C), two exponential terms (D) and Henderson & Pabis (E) to mesquite drying process at temperatures of 50˚C, 60˚C, 70˚C and 80˚C and in Tables 2-6 are estimated parameters for these models.
Observing Figure 2, it can be seen that during the drying of mesquite, as temperature is high, there is a major water removal of the product, besides reduction of drying time, allowing product to reach faster equilibrium water
![]()
Table 2. Coefficients obtained by fitting the Fick model to the experimental data of drying mesquite, at temperatures of 50˚C, 60˚C, 70˚C and 80˚C.
![]()
Table 3. Coefficients obtained by fitting the Page model to the experimental data of drying mesquite, at temperatures of 50˚C, 60˚C, 70˚C and 80˚C.
![]()
Table 4. Coefficients obtained by fitting the Cavalcanti-Mata model to the experimental data of drying mesquite, at temperatures of 50˚C, 60˚C, 70˚C and 80˚C.
![]()
Table 5. Coefficients obtained by fitting the Henderson & Pabis model to the experimental data of drying mesquite, at temperatures of 50˚C, 60˚C, 70˚C and 80˚C.
![]() (a) (b)
(a) (b)![]() (c) (d)
(c) (d)![]() (e)
(e)
Figure 2. Curves obtained by adjusting models Fick (a), Page (b) Cavalcanti Mata (c), Two Exponential Terms (d) and Henderson & Pabis (e) to drying process of mesquite, at temperatures 50˚C, 60˚C, 70˚C and 80˚C.
![]()
Table 6. Coefficients obtained by fitting the Two Exponential Terms model to the experimental data of drying mesquite, at temperatures of 50˚C, 60˚C, 70˚C and 80˚C.
content, which complies with studies with drying various products: rice [17] , pumpkin seeds [18] and mesquite grains [19] .
Still analyzing Figure 2, it is clear that drying occurred in the decreasing rate period; this phenomenon can be explained in the study of drying agricultural products, especially grain and seed, because it is known that these products have constant rate period of little or no drying, due to the occurrence of a difference between content of water in surface and in the interior of product. This is due basically to different migration speeds of the interior of water molecules to the periphery of product and evaporation of surface water molecules; this phenomenon has also been observed in coffee drying study [8] .
It is noticed that mesquite, with initial moisture content of 20% (b.u) led 1230, 990, 780 and 660 minutes to reach equilibrium moisture content: 7.0%, 6.5%, 6.0% and 5.5% (b.u) when subjected to drying process at temperatures of 50˚C, 60˚C, 70˚C and 80˚C, respectively. It is observed trend in the values of equilibrium water content when it decreases with increasing temperature, a fact that can be explained by the increase of the vapor partial pressure difference between drying air and product, so that increases mass transfer rate; this upgrade of energy to the process results in a higher excitation of water molecules, increasing the distance between them and reducing their attractive forces. This kind of behavior is typical of many agricultural products and has been observed in beans drying study [20] .
Diffusion model (2nd Law of Fick) was adjusted to experimental data using the first term of the series, therefore, from that term, diffusion coefficient and adjusting the curves showed very similar values.
It can be seen in Table 2, values of diffusion coefficient in mesquite drying temperatures of 50˚C, 60˚C, 70˚C and 80˚C ranged from 0.92 to 2.87 × 10−9 m2∙s−1. According to [21] values of diffusion coefficient for food materials are within a range of 10−11 to 10−9 m2∙s−1. [22] obtained by studying drying of turnip seeds, diffusion coefficient values ranging from 3.23 × 10−11 to 10.42 × 10−11 m2∙s−1 to temperatures of 30˚C and 70˚C, respectively. [23] verified, studying diffusivity of physic nut grain, values of magnitude of 9.24 × 10−10 to 41.48 × 10−10 m2∙s−1 to temperatures of 45˚C, 60˚C, 75˚C, 90˚C and 105˚C, respectively.
Diffusivity is understood as a physical phenomenon in which water migrates from center to surface material, and this parameter strongly influenced by drying temperature, as observed in this study, where: with increasing heat transfer rate occasioned by raising drying temperature, it was noticed a higher diffusion coefficient of mesquite. [24] observed the same behavior with increasing temperature gradient range finding diffusivity coefficient values of 0.181 to 2.90 × 10−10 m2∙s−1 to crambe seed, using temperatures from 30˚C to 70˚C with an initial moisture content of 22% (b.u).
It is noticed that the value of diffusivity drying temperature of 70˚C is about twice the value found for temperature of 60˚C; this numerical difference to the order of magnitude of 10−9 is justified because it is a biological material, wherein drying phenomenon cannot be generalized because they may have intrinsic characteristics that differentiate them from each other.
In Table 2, it appears that Fick model was adjusted satisfactorily to experimental data, with higher coefficients of determination that 98% and medium∙square deviation less than 0.03, with the exception of 80˚C, whose coefficient of determination was 98.86%. [25] also reported a good fit of Fick model to experimental data of cowpea drying at temperatures of 35˚C, 45˚C and 55˚C, obtaining a higher coefficient of determination error, and 99% on average less than 2% at all temperatures.
In Table 3, it is noted that parameters “K” and “n” of Page equation ranged from 0.0022 to 0.0056 and from 0.6138 to 0.7434, respectively, for temperatures of 50˚C and 80˚C and 70˚C and 60˚C. Drying constant value “K” showed increasing trend with increasing drying temperature. [26] considered that drying constant “K” can be used as an approximation to characterize drying air temperature effect on product and it is related to the effective diffusivity in drying process in the decreasing period and it is related to liquid diffusion that controls the process. In this study, it was observed that drying constant “K” obtained in four temperatures of Page model has similar behavior to diffusion coefficient found when applying Fick model.
It is observed in Table 3, that there is an increase of constant drying obtained at 70˚C, about twice the value obtained at drying temperature of 60˚C, explained in terms of heterogeneity of biological material; another explanation can be given by the energy that involves temperature of 70˚C, where for this energy, there is a greater transfer between partial pressure of water from mesquite steam and of drying air, due to structural barriers breakages of the heterogeneous composition of the product.
Still analyzing Table 3, it is clear that Page model was adjusted satisfactorily to experimental data yielded determination coefficients ranging from 99.76% (70˚C) to 99.90% (50˚C) and lower medium∙square deviation than 0.04 at all temperatures.
In literature it appears that Page model is quite successfully used in describing drying kinetics of various agricultural products, as several authors, including [17] , also observed by studying the kinetics of drying of rice in drying temperatures of 70˚C, 80˚C and 90˚C with air velocity of 1m∙s−1, that this model expresses satisfactorily the drying phenomena, obtaining coefficient determination of above 99% and medium∙square deviation of less than 0.05.
It can be seen in Table 4 that parameter “b” of Cavalcanti-Mata equation ranged from 0.0022 to 0.0041. The values of this constant behavior presented rising with increasing drying temperature. [19] observed the same behavior of parameter “b”, by applying Cavalcanti-Mata model to experimental data of drying grain of mesquite, at temperatures of 40˚C, 50˚C, 60˚C and 70˚C. Parameters “a1”, “a2”, “a3”, “a4” and “a5”, used in mathematical adjustments presented, in general, random behavior; however, Cavalcanti-Mata model represents experimental data in order exceeding 99% (correlation coefficients) and their medium∙squared deviations are smaller than 0.01 at all temperatures.
In Cavalcanti-Mata equation, the value of the parameter “b” is the effective diffusivity as well, since equation derived from model Fick to 2 terms of the series with time correction by means of potential coefficients a2 and a4. It is necessary to ask what the effective diffusivity should be considered or would be correct. It is noted that all coefficients are in the same order of magnitude. It is observed also that in Cavalcanti-Mata model, diffusivity data are more consistent because it is not found to exist values that are twice each other in drying function of temperature and there is a proportionality between these values, as observed in equidistance between drying curves.
In Table 5, it appears that drying constant “K” of Henderson & Pabis model ranged from 0.0036 to 0.0071, whose behavior was rising with increasing of drying temperature. This behavior is similar to that observed by [27] , wherein the values of “K” coefficient of variation increased to 30˚C temperature to 70˚C in a study of pumpkin seeds.
The parameter “a” of Henderson & Pabis model in case of mesquite pod varied from 0.8118 to 0.8838 between drying temperatures of 50˚C and 80˚C, noting a random behavior. [28] found by studying grapefruit seed drying kinetics, with drying temperatures of 40˚C, 50˚C, 60˚C and 70˚C and air velocity of 0.6, 1 and 1.4 m∙s−1, with values for parameter “a” ranging from 0.849 to 0.882.
In Table 5, it appears that model of Henderson & Pabis did not fit well to experimental data, showing larger determination coefficients of 96% and medium∙square deviation of less than 0.05 for all temperatures. [22] reported good fit of Henderson & Pabis model to experimental data of drying turnip at temperatures of 50, 60 and 70˚C and obtained coefficient of determination higher than 97% and medium relative error less than 0.7% at all temperatures.
It is observed in Table 6 that parameters “K0” and “K1” from two-term exponential model increased when temperature of drying increased from 50˚C to 80˚C; parameters “a” and “b” of the same model have randomized behavior for all drying temperatures of mesquite. [19] found values of “a” and “K1” with increasing of drying temperature, studying the kinetics of mesquite grain.
In Table 6, it is observed that two terms Exponential model is satisfactorily fitted to experimental data showing coefficients of determination higher than 99% and medium∙square deviation smaller than 0.02 for all temperatures. [29] found by studying the drying of corn on the cob at temperatures of 45˚C, 55˚C and 65˚C, good fit of two exponential model to experimental data obtained under a coefficient of determination higher than 99% and medium relative error less than 3%, at all temperatures. [25] also reported a good fit of two exponential model to experimental data terms of cowpea drying at temperatures of 25˚C, 35˚C, 45˚C and 55˚C, obtaining a coefficient of determination higher and 99% relative average error less than 1% at all temperatures.
4. Conclusions
Based on the results of drying mesquite, it is concluded that:
The drying mesquite occurred during the decreasing rate period, and with increasing drying temperature, there was a reduction in total process time, reaching the fastest equilibrium water content ranging from 7.0 5.5% to temperatures of 50˚C to 80˚C, respectively;
Diffusion coefficients, calculated from Fick model increased with increasing of drying temperature of 50˚C to 80˚C, with values of 0.92 to 2.87 × 10−9 m2∙s−1;
Mathematical models―Theoretical (Fick) and semi theoretical (Page and Cavalcanti-Mata) models satisfactorily represent the experimental data of mesquite drying at temperatures of 50˚C, 60˚C, 70˚C and 80˚C, with larger determining coefficients and 99% medium∙squared deviation less than 0.05 except for Fick model at temperature of 80˚C, where coefficient of determination was 98.86%;
The empirical model of Two Terms Exponential also provided good fit to the experimental data, showing coefficients of determination higher than 99% and lower medium∙square deviation 0.05;
Among the models studied, the model of Henderson & Pabis was presented the lowest determination coefficients ranging from 96.94% (70˚C) to 99.13% (60˚C).