Minimum Clearance Offsets for Providing Desired Stopping Sight Distances at Simple Curves with Variable Operating Speeds ()
Received 2 March 2016; accepted 12 April 2016; published 15 April 2016

1. Introduction
Provision of sufficient sight distance is one of the requirements for safe and efficient operation of highways. On straight sections of highways sight distance is naturally provided since sightlines are accommodated within travel lanes. At horizontal curves sightlines are not accommodated within lanes but on the inside of the curves. Presence of high roadside objects such as steep side-slopes in cut areas, buildings, trees, retaining walls, longitudinal safety barriers, etc. on the inside of horizontal curves may block the sightlines and degrade visibility of highway sections downstream of drivers. Blockage of the sightlines may reduce safety and mobility of the highways. To preserve safety and mobility design guidelines require that high objects on the inside of horizontal curves be cleared off. Methods of determining clearance widths (technically known as clearance offsets) needed to provide design sight distances are presented in design guidelines and other literature. Examples are: the graphical method in the AASHTO’s Green Book [1] , design charts by Raymond [2] and Glennon [3] , and the analytical model and its chart by Mauga [4] .
The graphical method in the AASHTO’s Green Book [1] , design charts by Raymond [2] and Glennon [3] , and the analytical model by Mauga [4] are known for determining minimum offsets that provide a given fixed or constant design sight distance. The fixed or constant design sight distance is so since it is calculated from a fixed or constant design speed. The assumption is that drivers travel at constant speed along horizontal alignments (i.e. have cruise control on). Therefore, the models are suitable for sites where drivers travel at constant speed. However, past studies have shown that there are sites at which vehicles travel at high speed on approach tangents upstream of curves, decelerate on entering the curves, accelerate on leaving the curves, and continue to travel at high speeds on departure tangents downstream of the curves [5] . At those sites sight distance demands or desires vary with driver location. Sections near beginnings and ends of curves need wider clearance offsets so as to provide longer sight distances that match high operating speeds. Where operating speeds are higher than design speeds [6] clearance offsets that are wider than design offsets may be applied so as to accommodate longer desired sight distances. Models for determining those wide offsets are needed.
The only current model that may be addressing wide clearance offsets for beginnings and ends of horizontal curves is the simple analytical model by the Green Book [1] as presented by Equation (1). This model is mainly suitable for middle sections of curves but the guideline suggests that it be applied uniformly along curves. Although the intension is not to provide long sight distances, it may be serving that purpose. Wood and Donnell [7] conducted an analysis to support uniform application of the offset in Equation (1) within horizontal curves. Their rationale was consistency defined as no difference in probability of drivers’ noncompliance between tangent and curved sections. I agree that use of the offset given by Equation (1) at beginnings and ends of curves will provide greater sight distances that accommodate high speeds on approach tangents and acceleration at ends of curves. However, I am of the opinion that offsets determined with Equation (1) may still be greater than minimum offsets needed to provide longer sight distances for speeding drivers. Offsets that are significantly greater than minimum values have cost implications especially in cut zones.
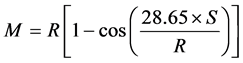 (1)
(1)
where
M is the minimum offset measured from driver path;
R is the radius of curved driver path;
S is the design sight distance.
Objectives of this paper are three. First, to propose an analytical model for minimum offsets that when applied at beginnings and ends of curves desired sight distances (not necessarily minimum) will be available to drivers that are speeding on approach tangents and at ends of curves. The minimum offsets will serve as lower boundary values for checking offsets suggested by designers based on criteria such as roadside aesthetics and others. Second, to suggest a design chart for determination of the offsets. Third, to identify a known curve that approximates the roadside clearance envelopes that result when those minimum offsets are implemented in the field.
2. Graphical Solution
The general and intuitive solution to variable sight distance demands at a given curve is the use of the graphical method suggested in the Green Book. The method consists of manually drawing sightlines that start at many driver locations and end at downstream locations that are located at distances equal to desired sight distances. The procedure was demonstrated by Glennon [3] for constant design sight distance but here the procedure is modified by considering variable desired sight distances for each driver location. The term “desired” is used in place of “design” in order to match with drivers’ desired speeds which may be greater than design speed. The desired sight distances are calculated based on desired drivers’ speeds at each location. Figure 1 illustrates the graphical method. The dashed lines in the figure are a representation of two sightlines. Sightlines that originate within the approach tangent and end within the curve are expected to be longer than those originating and ending within the curve. It is because drivers have high speeds on tangents and low speeds within curves.
After the sightlines are drawn, a curve that is tangential to all sightlines is drawn. This curve is a clearance envelope and it is a boundary that marks the roadside area that accommodates sightlines for desired sight distances. To obtain clearance offsets a designer measures lengths of normal ordinates from driver path to the clearance envelope. Lines AB and CD in Figure 1 are examples of offsets at stations A and C, respectively.
In Figure 1, the envelope consists of three arcs for sites where curved driver paths are longer than desired sight distances. The first arc is between station PC − S1 and station B where S1 is the sight distance desired by drivers on the approach tangent. That arc has a radius that decreases gradually from infinity at PC − S1 to R-M at B where M is the desired offset determined with Equation (1). The second or middle arc is between B and D and is a circular arc with radius R-M. The third arc is between D and PT + S2 where S2 is the sight distance desired by drivers at PT. The third arc has a radius that increases from R-M at point D to infinity at PT + S2.
The envelope arcs that have variable radii in Figure 1 are of unknown functional form so far. But for sites with constant driver speeds the arcs are some form of spirals. Olson et al. [8] called the two arcs transition curves for lateral clearance. The words “for lateral clearance” imply that Olson et al. knew that the transition curves were not the Euler’s spirals that are used for transitioning horizontal alignment. Those envelope transition curves or spirals should not be confused with the Euler’s spirals or many other spirals such as the Archimedean spiral [9] , hyperbolic spiral, logarithmic spiral, etc. These spirals have different geometric properties and hence functional forms but the commonplace of all spirals is that radii change inversely proportional to lengths.
The graphical procedure is intuitive and accurate but it is also time consumming. To solve the problem of time consumption mathematical representation of the method is developed in the next section. Derivation starts with mathamatical representation of the clearance envelope in Figure 1. Then envelope equations are used to derive equations for offsets.
3. Analytical Solution
This section presents derivation of mathematical equations for the roadside clearance envelope and offsets that should equal the offsets determined with the graphical procedure. Graphical offsets are the target since the graphical procedure is the original, accurate, and intuitive solution to the roadside clearance on the inside of horizontal curves but also it has been recommended by the Green Book and accepted by researchers and practitioners. Previous analytical models and charts for minimum offsets were all developed by imitating the graphical procedure [2] - [4] .
![]()
Figure 1. Graphical method for determining minimum offsets.
Derivation of the analytical model considers the highway section from station PC − S1 to PT + S2 since this section is where high roadside objects on the inside of horizontal curves have negative impact on road visibility. The derivation considers two cases where the first case is for highway curves that are longer than sight distances desired by drivers when the drivers are at PC. The second case is for highway curves that are shorter than sight distances desired by drivers when the drivers are at PC.
3.1. Case 1: Long Curves
Derivation of equations for the clearance envelope is through modifying equations that were derived by Mauga [4] . The equations in [4] were derived for design speeds and hence constant design sight distances. Constant design sight distance implies that a driver cruising at design speed watches a downstream car that is also cruising at design speed and the two cars are separated by a distance that equals design sight distance. Equation (2) presents the equation developed in [4] . The clearance envelope corresponding to Equation (2) is termed here as the constant-S envelope.
 (2)
(2)
where
TH is the horizontal length of a sightline from driver eyes to the point of tangency on the envelope;
d is the driver location from PC − S;
TM is TH when drivers are within the section between PC and PT − S,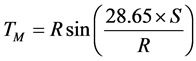 ;
;
L is the length of curve;
C1 is a constant given by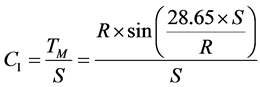 ;
;
C2 is a constant given by ;
;
PC is point of curvature;
PT is point of tangency.
The first and third regimes of Equation (2) are spiral arcs described by sightline tangent length TH as a linear function of driver location d. These arcs are grouped as spirals since they have radii changing with lengths. But the arcs are different from the Euler’s spiral in the aspect of functional form and geometric properties such as curvature. Moreover, the Euler’s spiral does not match construction of the graphical method in Figure 1 hence it is not suitable for determining minimum clearance offsets for given sight distances [4] . The second regime is a circular arc of radius R-M. The regime is described by the constant term that is equal to half the length of a sightline.
Modification of Equation (2) is done through first, making variable the term S for sight distance in all terms of Equation (2) that contain S. The variable sight distance is thus denoted by Sd as seen in Equation (3). Second, regimes 2 and 3 are modified by factors  and
and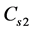 , respectively. The clearance envelope corresponding to Equation (3) is thus termed as the variable-S envelope.
, respectively. The clearance envelope corresponding to Equation (3) is thus termed as the variable-S envelope.
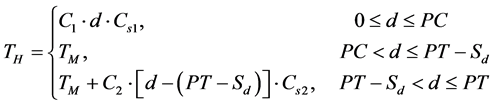 (3)
(3)
where
C1 is given by ;
;
Sd is the desired sight distance for a driver at location d;
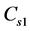 modifies driver location to that measured from PC − Sd,
modifies driver location to that measured from PC − Sd,  is given by
is given by ;
;
S1 is the desired sight distance based on tangent speeds;
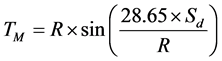 ;
;
C2 is given by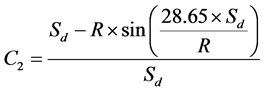 ;
;
![]() modifies location of end of a sightline to that measured from PT + S2,
modifies location of end of a sightline to that measured from PT + S2, ![]() is given by
is given by![]() ;
;
S2 is the desired sight distance for a driver at PT.
The geometric meaning of Equation (3) is that the variable-S envelope is a curve that spans across many clearance envelopes that are based on constant S values. Figure 2 illustrates the way the curve for Equation (3) spans across constant-S envelopes. The variable-S envelope starts at PC − S1 then spans across envelopes until it merges with the envelope for minimum S. Then it spans across the other envelopes up to PT + S2. At a point of intersection of the variable-S envelope and a constant-S envelope is where values of Sd are equal to constant S. Therefore, Equation (2) is for specific cases of Equation (3) i.e. Equation (3) turns into Equation (2) if![]() .
.
3.2. Case 2: Short Curves
The equation for the clearance envelope is obtained through accordingly applying modifications to Equation (19) in [4] .
3.3. Equations for Offsets
Offsets are calculated using Equation (29) presented by Mauga [4] . The equation is presented below as Equation (4a). The first regime of the equation has been added here to account for locations where clearance provided by lanes, shoulders, and clear zone is greater than those determined with regimes 2, 3, and 4. PC − S1 is considered as the origin of the horizontal x-y coordinate where x-axis is the approach tangent and y-axis is positive on the inside of a curve consistent with positive sign of offsets.
![]()
Figure 2. Geometric meaning of the variable-S envelope and Equation (3).
![]() (4a)
(4a)
where
![]() is the normal offset in plan view;
is the normal offset in plan view;
![]() is the lateral width of clear zone on a tangent, m0 is measured from driver path;
is the lateral width of clear zone on a tangent, m0 is measured from driver path;
![]() is the central angle of the horizontal curve;
is the central angle of the horizontal curve;
![]() is the angle as shown in Figure 3,
is the angle as shown in Figure 3,![]() ;
;
X is the offset station measured from PC − S1;
x is the x-coordinate of the envelope,![]() ;
;
y is the y-coordinate of the envelope,![]() ;
;
![]() is the x coordinate of a driver or beginning of a sightline;
is the x coordinate of a driver or beginning of a sightline;
![]() is the y coordinate of a driver or beginning of a sightline;
is the y coordinate of a driver or beginning of a sightline;
![]() is the angle between a sightline and the approach tangent,
is the angle between a sightline and the approach tangent,![]() ;
;
![]() is the x coordinate of the end of a sightline;
is the x coordinate of the end of a sightline;
![]() is the y coordinate of the end of a sightline.
is the y coordinate of the end of a sightline.
The location of an offset is given by Equation (4b)
![]() (4b)
(4b)
![]()
Figure 3. Relationship between terms of regime 4 in Equation (4a).
4. Example
Consider a two lane highway with posted speed of 50 mph. At an isolated horizontal curve the driver path has a radius of 650 ft and a curved length of 600 ft. The pavement is a high friction surface with a superelevation of 8%. On tangent sections the highway has 3 ft paved shoulders and 3ft untreated shoulders. The roadside on the inside of the curve is to be cleared to accommodate up to 90th percentile speeds. The 90th percentile is used here only as an example of high percentile speed (since the Green Book suggests that designs be based on high percentile speeds) but designers may choose other high percentiles such as the 80th, 85th or any other percentile that best matches their jurisdictions’ needs. To estimate tangent and curve 90th percentile speeds Equation (6.9) and Equation (6.10) from the report by Medina and Tarko [10] are used. Transition speeds are calculated using Equation (6.11) also from the report by Medina and Tarko [10] . Figure 4 presents the 90th percentile speed profile and the profile of stopping sight distance (SSD) calculated using the 90th percentile speeds.
Stopping sight distances in Figure 4 are input to Equations (2), (3) and (4) to yield offset profiles. Figure 5 presents profiles of minimum offsets for variable-S as well as for four constant-S values. Values on the horizontal axis are not driver locations but locations of offsets that will provide desired sight distances for drivers upstream of the locations. Figure 5 also shows that the offset profile for variable-S envelope spans across profiles of the four constant-S offsets. Figure 5 is another way of presenting how the variable-S envelope spans across constant-S envelopes as presented earlier in Figure 2.
![]()
Figure 4. Profiles of 90th percentile speeds and stopping sight distances.
![]()
Figure 5. Profiles of minimum offsets for variable and constant stopping sight distances.
Figure 5 also presents the profile of minimum offsets determined with the graphical method for the variable-S envelope. It is apparent that offsets determined with the (variable-S) analytical model are in agreement with offsets determined with the graphical method. Agreement of the offsets validates the analytical model since the graphical method is considered accurate and has been recommended by the Green book and accepted by researchers and practitioners.
5. Design Chart
It is proposed that the design chart developed by Mauga [4] also be used for determining offsets at sites with variable sight distance demands. Although the chart was developed for constant-S envelopes, its L/S and m/M ratios allow offsets for variable-S envelopes to be determined. However, the location ratio is modified from
X/(2S + L) for constant-S to ![]() for variable-S where X is location of an offset measured
for variable-S where X is location of an offset measured
from PC − S1. This modification necessitates a user to know desired sight distance S at each location before using the chart. For the example in Section 4 the relationship between desired sight distance and offset location is given by Figure 6. Values on the horizontal axis of the figure were determined with Equation (4b). Figure 6 is necessary only for variable-S envelopes and is not needed for cases of constant-S envelopes.
Table 1 below presents how offsets are determined from the chart for the example given in section 4 above. Inputs to the chart are the location ![]() and L/S ratios in columns 5 and 6, respectively.
and L/S ratios in columns 5 and 6, respectively.
![]()
Figure 6. Relationship between offset location and desired stopping sight distance.
![]()
Table 1. Use of design chart to determine offsets.
The output is the m/M ratio in column 7. The offset M in column 8 is determined with Equation (1) for each S in column 3. The m/M ratio is multiplied by M to obtain offsets in the last column. The offsets determined are for locations where required offsets are greater than the clear zone of 12 ft used in the example.
Figure 7 below shows how the values of the m/M ratios in Table 1 have been obtained as a function of location ![]() and L/S ratios. The x-markers are for locations or stations in Table 1 above and
and L/S ratios. The x-markers are for locations or stations in Table 1 above and
the green dashed line joining the markers is for all points making the envelope for the example in Section 4 above. It is worth to note that the chart includes low values of m/M ratios as a reservation for variable clear zone mo since the ratio mo/M can vary within a site as well as among sites.
6. Comparison with Other Envelopes
The Green Book [1] suggests that constant offsets determined with Equation (1) be applied uniformly all over the inside of a horizontal curve. Wood and Donnell [7] explained an advantage of applying such long offsets near beginnings and ends of horizontal curves as that long offsets provide sufficient sight distances for speeding drivers on approach tangents and for accelerating drivers as they depart from the curves. Examining the offsets in Table 1 and the offset ratios m/M in Figure 7 reveals that the minimum offset at PC is smaller than the middle offset at PC + 0.5L by approximately 20 ft despite longer desired sight distances on the tangent than within the curve. This difference in length of the two offsets supports my opinion that minimum offsets required to provide a desired sight distance at PC and PT are smaller than offset M for middle sections of curves. However, the suggestion by the Green Book and by Wood and Donnell [7] that design offsets determined with Equation (1) be used at PC and PT is accurate to some extent. Plugging the design sight distance of 425 ft in Equation (1) yields an offset of 34.43 ft. The 34.43 ft offset is only slightly greater than minimum offsets of 31.69 ft and 30.54 ft needed at PC and PT, respectively, hence there is sufficient sight distance for drivers on the approach tangent and for drivers near the end of the curve. Figure 8 presents profiles of available sight distances determined with the variable-S envelope, uniform-M envelope, uniform-M-plus-straight envelope, and the profile of calculated desired stopping sight distance. The uniform-M envelope is the clearance boundary formed by applying uniformly the design offset of 34.43 ft within the curve as well as on the tangents. The uniform-M-plus- straight envelope is the clearance boundary formed by applying uniformly the design offset of 34.43 ft within the curve but with two transition straight sections. One straight section transitions the clear zone mo from PC − 0.5S (where S = 425 ft) to the offset M at PC and the other straight section transitions the offset M at PT to mo at PT + 0.5S. A number of agencies use the straight sections in order to avoid applying the wide offset M on tangents where sightlines are already accommodated within travel lanes. The profile of calculated SSD and the profile of available sight distances for the variable-S envelope merge and diverge where calculated offsets to sight- lines are equal to the clear zone mo (measured from driver path).
![]()
Figure 7. Design chart for clearance offsets, R/S = 1.25.
![]()
Figure 8. Profiles of available sight distances and desired stopping sight distance, L > SPT.
In Figure 8, it is apparent that the uniform-M envelope provides longer sight distances for drivers travelling at high speeds on the approach tangent as well as near the end of the curve. The uniform-M-plus-straight envelope provides sight distances that are approximately equal to those of the variable-S envelope for drivers on the approach tangent and for drivers near the end of the curve. The only problem with the uniform-M envelope and its cousin is that the 34.43 ft design offset doesn’t consistently provide sufficient sight distances for drivers travelling at high percentile speeds within the curve. Uniform use of the design offset would be suitable at sites where vehicles decelerate significantly on approaching the curves such that high percentile speeds within the curve are equal to or less than posted speeds (i.e. sight distances demanded are equal to or smaller than provided design sight distances within the curve).
Wood and Donnell [7] also stated (contextually) that offsets determined with clearance spirals for PC are unsuitable for accommodating long sight distances demanded by speeding drivers on approach tangents. It has been demonstrated in this paper that the chart in Figure 7 (which was developed with clearance spirals for constant sight distances) is also applicable for sites with variable operating speeds. The chart uses location ratio ![]() and length ratio L/S as inputs. These ratios generalize the chart such that it works for any sight distance determined with any percentile speed as long as its clearance envelope is determinable by the graphical procedure in Figure 1. For example, Wood and Donnell [7] suggested that a sight distance of 467.2 ft be provided at PC for case 1 in Table 2 in their paper [7] so that the probability of noncompliance of 0.193% at PC would be lowered to 0.0001% (which is for the middle of the curve). Plugging 425 ft (i.e. the design value of stopping sight distance for case 1 in [7] ) in Equation (1) results in an offset of 29.52 ft. The 29.52 ft is the offset they would suggest be applied uniformly within the curve. An offset chart with R/S ≥ 1.5 by Mauga [4] or the graphical procedure suggests the minimum offset of 21.4 ft at PC in order to provide the 467.2 ft sight distance. The driver location corresponding to the 21.4 ft offset is PC-153.1 ft. Therefore, the 29.52 ft offset at PC works since it provides more than minimum desired sight distance but as a matter of principle it is not the minimum offset required to provide the 467.2 ft sight distance.
and length ratio L/S as inputs. These ratios generalize the chart such that it works for any sight distance determined with any percentile speed as long as its clearance envelope is determinable by the graphical procedure in Figure 1. For example, Wood and Donnell [7] suggested that a sight distance of 467.2 ft be provided at PC for case 1 in Table 2 in their paper [7] so that the probability of noncompliance of 0.193% at PC would be lowered to 0.0001% (which is for the middle of the curve). Plugging 425 ft (i.e. the design value of stopping sight distance for case 1 in [7] ) in Equation (1) results in an offset of 29.52 ft. The 29.52 ft is the offset they would suggest be applied uniformly within the curve. An offset chart with R/S ≥ 1.5 by Mauga [4] or the graphical procedure suggests the minimum offset of 21.4 ft at PC in order to provide the 467.2 ft sight distance. The driver location corresponding to the 21.4 ft offset is PC-153.1 ft. Therefore, the 29.52 ft offset at PC works since it provides more than minimum desired sight distance but as a matter of principle it is not the minimum offset required to provide the 467.2 ft sight distance.
In general, geometry of a roadside clearance envelope is dependent on the functional form of the speed transition model as drivers approach curves or depart from the curves. The speed transition model used in this paper is linear [10] and the corresponding variable-S clearance envelope is approximated by a circular arc sandwiched between two transition elliptical arcs. One of the elliptical arcs is on the approach side and the other on the departure side. Figure 8 shows that the available sight distance profile for the variable-S envelope is closer to that of the envelope with elliptical transition arcs than to other profiles. Further analysis of the elliptical transition arcs revealed that the arcs also approximate constant-S envelopes but the approximation is not better than that of variable-S envelopes.
Other than being aesthetical, one benefit of the elliptical transition arcs is that they seamlessly transition clearance from any clear zone or shy-line offset on tangents to the offset M determined with Equation (1). The equation of the approach elliptical arc used for the profile in Figure 8 is given by Equation (5) considering a local origin at PC − Smin. The numbers 303.67 and 693.57 are calibration values specific only to the example presented in Section 4. These numbers were obtained by fitting in the general equation of an ellipse coordinates (0.5Smin, mo) where the arc is tangential to the edge of the clear zone and also fitting the (x, y) coordinates of the circular part of the envelope at PC + 0.5Smin. The elliptical arc on the departure side was determined through reflection of the approach elliptical arc on the line of symmetry joining the point of intersection of tangents (PI) and station PC + 0.5L. The elliptical arc on the departure side ends at PT + 0.5Smin where the arc is tangential to the edge of the clear zone. Offsets to the elliptical arcs may be determined analytically since their geometric formulae are known or the offsets may be determined using the design chart in Figure 7. For example, the offset at PC is for a sight line with an available sight distance of 537.26 ft which corresponds to driver location at PC − 195.38 ft. An offset ratio m/M for that location is 0.606. Multiplying this offset ratio with the middle offset of 54.72 ft (determined by pugging S = 537.26 ft in Equation (1)) yields an offset of 33.18 ft. This 33.18 ft offset is comparable to 31.69 ft in Table 1 for PC.
![]() (5)
(5)
![]() (6)
(6)
where
Smin is the minimum desired SSD within the curve;
SM is the SSD corresponding to M at sites with short curves;
![]() is the lateral clear zone measured from driver path, here
is the lateral clear zone measured from driver path, here![]() .
.
Equation (6) is for an elliptical envelope at a site like that in the example in Section 4 but with a 300 ft highway curve. Two elliptical transition arcs meet on the roadside at PC + 0.5L and there is no circular arc between the elliptical arcs. Figure 9 shows how available sight distances corresponding to the elliptical envelope are closer to the variable-S envelope’s than the other two envelopes. M in the legends of the two other envelopes is not determined with Equation (1) but with the equation for the middle offsets for sites with short curves. The uniform-M envelope has M applied uniformly within the curve and on tangents whereas the M-plus-straight envelope has two straight transition sections meeting on the roadside at PC + 0.5L. Note that all available sight distance profiles in Figure 8 and Figure 9 assume that a vehicle that is downstream of the subject driver is
![]()
Figure 9. Profiles of available sight distances and desired stopping sight distance, L < SPT.
very far such that it is out of sight of the subject driver hence the subject driver sees only the roadway and roadside surroundings. When there are vehicles within the sight of the subject driver the available sight distance is simply the spacing between vehicles.
7. Conclusion
Design guidelines require that the roadside area on the inside of horizontal curves be cleared of sight obstructions. One of the guidelines, the Green Book, has an analytical model for determining the minimum extent of clearance. The guideline suggests use of the graphical method where designers feel that the guideline’s model is unsuitable. The graphical method is intuitive and accurate but it is slow. This paper presents derivation of an analytical representation of offsets determined with the graphical method for sites with variable operating speeds. It also presents a design chart for determining minimum clearance offsets. It is worth noting that the words “minimum clearance offset” do not necessarily mean an offset for providing minimum sight distance but rather smallest offset needed to provide a given sight distance. Minimum offsets are low boundary values for checking suitability of offsets proposed by designers. Use of the minimum offsets at sites with variable operating speeds will yield roadside clearance boundaries that have transition arcs with geometric properties that can be approximated by those of elliptical arcs. Designers may choose to permanently mark elliptical clearance boundaries since their equations are known or the designers may use offsets determined with equations derived in this paper or offsets determined with the suggested design chart.