Received 30 November 2015; accepted 27 March 2016; published 30 March 2016

1. Introduction
Malaria is one of the leading causes of morbidity and mortality in Kenya and it kills an estimated 34,000 children under five every year. Economically, it is estimated that 170 million working days in Kenya are lost each year because of malaria illness.
http://kenya.usaid.gov/programs/health/72.
After 1990, pyrethroids were promoted as insecticides of choice especially for Insecticides Treated Nets (ITNs) and Indoor Residual Spray (IRS) [1] [2] , due to high efficacy, rapid rate of knockdown, strong mosquito excito-repellence and low mammalian toxicity [3] .
In Kenya, ITNs have mainly been distributed to pregnant women and children under 5 years old by the Kenya Ministry of Health and non-governmental organizations [4] [5] . Currently, ITN coverage for children under 5 years old has increased rapidly from 7% in 2004 to 67% in 2006; this increase has been associated with a 44% reduction in malaria deaths [6] . However there is an increasing case resistance of mosquitoes to pyrethroid. The likely zoonotic nature of P. falciparum and the behavioral changes of mosquitoes are many new features which indicate that malaria control is not yet achieved [7] - [9] . The gains made from ITNs and IRS therefore are threatened by the development of physiological or behavioral resistance in the malaria vectors, which is widely documented [10] . Anopheline mosquitoes exhibit two major mechanisms of pyrethroid resistance, they are:
1) Increased level of metabolic detoxification of the insecticide,
2) Reduced sensitivity in the target sites of the insecticide. The target site of the pyrethroids is the voltage- gated sodium channel.
The second type of resistance is caused when a point mutation in the region II of the para-type sodium channel genes causes a change in affinity between the insecticide and its binding site or the sodium channel, and it induces a phenotype termed knock-down resistance (KDR) in a range of insecticides [11] - [14] . Insensitivity at the sodium channel target site also leads to cross-resistance between different classes of insecticides [15] .
Reports from literature confirm that use of ITNs and IRS has led to a substantial reduction in mosquitoes, reduced malaria transmission and a 44% reduction in malaria deaths [16] - [18] . However, although there was a global reduction in overall malaria transmission, 57% of the population continued to live in areas where transmission remained moderate to intense in Africa [19] . The ITNs and IRS intervention can reduce malaria transmission by targeting mosquitoes when they feed upon sleeping humans and/or rest inside houses, livestock shelters or other man-made structures. Despite high coverage, malaria spreading mosquitoes can maintain robust transmission because they develop resistance hence limiting the achievable impact [20] [21] . High and patchy resistance to pyrethroid insecticide has been confirmed in the endemic region of western Kenya, leaving the government with limited option but to seek other control measures [7] .
In this study, we develop a mathematical model with two types of vectors, one which is sensitive to the insecticides and a resistant type which adapts easily and survives despite the two types of intervention. We assume that the An. fambiae and the An. fenestus mosquito species are either sensitive or resistant to insecticides.
In section 2 we develop the model and equations. In section 3 the basic properties of the model are shown for positive invariance and computation of the basic reproduction number is also done. Section 4, we show the local and global stability of the Disease Free Equilibrium and section 6 is the conclusion.
2. The Model Formulation and Equations
We shall subdivide the mosquito population in Western Kenya into the traditional (non resistant) group and the new resistant group. This new resistance type has been termed as a “super mosquito”, but for the sake of terminology, we shall refer to them generally as “resistant” mosquito vectors. We shall use the subscripts “n” to represent non resistant traditional vectors, while, “r” represents the resistant vectors.
In this model 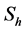 will represent the susceptible human hosts while
will represent the susceptible human hosts while 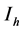 will represent the infectious human population. The variable
will represent the infectious human population. The variable  representing the total human population will be given by
representing the total human population will be given by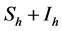 . The non resistant susceptible (infectious) vectors will be represented by
. The non resistant susceptible (infectious) vectors will be represented by 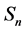 (
(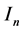 ), respectively, while the resistant vector population will be represented likewise as
), respectively, while the resistant vector population will be represented likewise as  (
(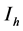 ), for the susceptible (infectious) population respectively. The total non resistant vector, therefore is given by
), for the susceptible (infectious) population respectively. The total non resistant vector, therefore is given by 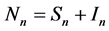 and the resistant vector population by
and the resistant vector population by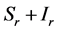 . We shall use
. We shall use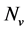 , reservedly for the total resistant and non resistant vector populations respectively, hence
, reservedly for the total resistant and non resistant vector populations respectively, hence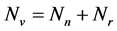 .
.
When there are no malaria deaths, the host population dynamics is given by![]() , and the total
, and the total
human and mosquito population size ![]() approaches a carrying capacity
approaches a carrying capacity ![]() for any non zero initial pop-
for any non zero initial pop-
ulation size.
The non-resistant vector population defined by ![]() approaches a carrying capacity
approaches a carrying capacity![]() , while the resistant vector population approaches a carrying capacity
, while the resistant vector population approaches a carrying capacity![]() .
.
Model assupmtions:
the two types of vectors have different biting rates hence differentiated infectivity,
the two types coexist and no vector changes status during the entire life span, i.e. not resistance vector becomes non-resistant or vice versa,
The total vector and human populations are constant.
The following parameter symbols will be used in the equations:
![]() : The per capita rate of human birth,
: The per capita rate of human birth,
![]() : The per capita rate birth rate of traditional vector and resistant vector respectively,
: The per capita rate birth rate of traditional vector and resistant vector respectively,
![]() : The proportion of infectious bites on hosts that produce a patent infection,
: The proportion of infectious bites on hosts that produce a patent infection,
![]() : The proportion of bites by susceptible vectors on infectious hosts that produce a patent infection,
: The proportion of bites by susceptible vectors on infectious hosts that produce a patent infection,
![]() : The per capita death rate for the human, traditional and resistant vectors, respectively,
: The per capita death rate for the human, traditional and resistant vectors, respectively,
![]() : Hosts rate of recovery,
: Hosts rate of recovery,
![]() : The man biting rates of traditional and resistant vector, respectively.
: The man biting rates of traditional and resistant vector, respectively.
The dynamics of our model will be governed by the following set of equations:
![]() (1)
(1)
The term ![]() in the susceptible host’s compartment corresponds to a constant recruitment of susceptible hosts by natural birth.
in the susceptible host’s compartment corresponds to a constant recruitment of susceptible hosts by natural birth.
The transmission term ![]() corresponds to frequency dependent infection of susceptible hosts by infectious non resistant mosquitoes, on infection they move to the infectious compartment.
corresponds to frequency dependent infection of susceptible hosts by infectious non resistant mosquitoes, on infection they move to the infectious compartment.
The transmission term ![]() corresponds to frequency dependent infection of susceptible hosts by infectious resistant mosquitoes, on infection they also move to the infectious compartment.
corresponds to frequency dependent infection of susceptible hosts by infectious resistant mosquitoes, on infection they also move to the infectious compartment.
The infected hosts who recover ![]() become susceptible again as malaria has no permanent immunity.
become susceptible again as malaria has no permanent immunity.
The last terms ![]() represents per capita deaths of the susceptible, infected hosts respectively.
represents per capita deaths of the susceptible, infected hosts respectively.
In the susceptible vectors, ![]() represent the recruitment of susceptible non-resistant, (resistant) mosquitoes, respectively, by birth.
represent the recruitment of susceptible non-resistant, (resistant) mosquitoes, respectively, by birth.
The term ![]() corresponds to the transmission of malaria to an susceptible non-resistant, (resistant) vectors, respectively, by an infected host.
corresponds to the transmission of malaria to an susceptible non-resistant, (resistant) vectors, respectively, by an infected host.
Natural deaths affects all the groups as denoted by the parameter ![]() for the susceptible non- resistant, (resistant) vectors respectively, and
for the susceptible non- resistant, (resistant) vectors respectively, and ![]() for the infectious non-resistant, (resistant) vectors respectively.
for the infectious non-resistant, (resistant) vectors respectively.
Both resistant and non resistant vectors, once infected, are assumed to remain infected till death as mosquitoes do not recover or develop immunity from the parasite [22] [23] .
All the parameters in the model are non negative and the model equations are well posed.
Equation (1) is defined in feasible region
![]()
where ![]() denotes the non-negative cone of
denotes the non-negative cone of ![]() including its lower dimensional faces. It is clear that Ω is positively invariant with respect to (1). We denote the boundary and the interior of Ω by
including its lower dimensional faces. It is clear that Ω is positively invariant with respect to (1). We denote the boundary and the interior of Ω by ![]() and
and ![]() respectively.
respectively.
3. Well-Posedness of System
We use the relation ![]() and
and![]() , and
, and ![]() to reduce Equation (1), and therefore study the system
to reduce Equation (1), and therefore study the system
![]() (2)
(2)
3.1. A Compact Positively Invariant Set
In this section we prove that the following set
![]()
is a positively invariant compact set for system (2) by barrier theorems (e.g. [24] [25] ). Moreover ![]() is a global attractor on the nonnegative orthant
is a global attractor on the nonnegative orthant ![]()
Now we show that the vector field induced by the system is either tangent or entering ![]() on the boundary
on the boundary![]() .
.
![]() ;
;
when ![]() and
and ![]() we have
we have![]() .
.
![]() and
and![]() ;
;
![]() and
and![]() ;
;
since ![]() we have
we have![]() ;
;
since ![]() we have
we have![]() ;
;
when ![]() and
and ![]() we have
we have![]() ;
;
when ![]() and
and ![]() we have
we have![]() ;
;
We denote the demographic equilibria by![]() ,
, ![]() and
and![]() .
.
The total human population is given by![]() . In the absence of the disease
. In the absence of the disease ![]() and the equation becomes
and the equation becomes![]() , which can be written as
, which can be written as
![]()
The Integrating factor for this linear differential equation is given by
![]()
Thus
![]()
Integrating both sides we and applying the intial conditions (![]() ) we have
) we have
![]()
The Equation for the Traditional non reistant mosquito ![]() is given by
is given by![]() , which can be written as
, which can be written as
![]()
The Integrating factor for this linear differential equation is given by
![]()
Thus
![]()
Integrating both sides we and applying the intial conditions (![]() ) we have
) we have
![]()
Finally, the equation for the resistant mosquito given by![]() , can be written as
, can be written as
![]()
The Integrating factor for this linear differential equation is given by
![]()
Thus
![]()
Integrating both sides we and applying the intial conditions (![]() ) we have
) we have
![]()
Thus the feasible set for the model system (1) is given by![]() , which is a positively invariant set. Hence the model is well posed and biologically meaningful.
, which is a positively invariant set. Hence the model is well posed and biologically meaningful.
3.2. Basic Reproduction Number
![]()
![]()
![]() (3)
(3)
which can be simplified as
![]() (4)
(4)
The expression ![]() is caled the basic reproduction number, with a biological meaning that is can be inter-
is caled the basic reproduction number, with a biological meaning that is can be inter-
preted from terms under the square root sign. The first term![]() , represents the number of secondary human infections caused by one infected resistant and one none resistant mosquito vector. The term
, represents the number of secondary human infections caused by one infected resistant and one none resistant mosquito vector. The term ![]() represents the number of secondary mosquito infections caused by one infected human to an non-resistant vector, while
represents the number of secondary mosquito infections caused by one infected human to an non-resistant vector, while ![]() represents the number of secondary infections to a resistant mosquito vector by a hu-
represents the number of secondary infections to a resistant mosquito vector by a hu-
man host. The square root sign represent the two generations that the disease has to undergo from a mosquito to a human being and to a mosquito again or vice versa for the infection to take place. It is a number that determines the threshold for disease spread, as well as a control tool that whose parameters can be targeted for control.
4. Stability of Disease-Free Equilibrium Solution
Jacobian evaluated at disease-free equilibrium solution:
![]()
Characteristic polynomial:
![]() (5)
(5)
where
![]()
![]()
![]()
![]()
it is easy to show that
![]()
which is positive if![]() .
.
![]()
This means all the roots of the polynomial equations are negative, hence the system is locally asymptotically stable.
Global Stability of the DFE
The local dynamics of a general SIS and SI model is determined by the reproduction number![]() . If
. If![]() , then each infected individual in its entire period of infectiousness will produce less than one infected individual on average. This means that the disease will be wiped out of the population. If
, then each infected individual in its entire period of infectiousness will produce less than one infected individual on average. This means that the disease will be wiped out of the population. If![]() , then each infected individual in its entire infectious period having contact with susceptible individuals will produce more than one infected individual implying that the disease persists in the population. If
, then each infected individual in its entire infectious period having contact with susceptible individuals will produce more than one infected individual implying that the disease persists in the population. If![]() , and this is defined as the disease threshold, then one individual infects one more individual. For
, and this is defined as the disease threshold, then one individual infects one more individual. For ![]() the disease free equilibrium is locally asymptotically stable while for
the disease free equilibrium is locally asymptotically stable while for ![]() the disease free equilibrium becomes unstable. By using the theory of Lasalle-Lyapunov function V, we will show the global asymptotic stability. The disease free equilibrium point is
the disease free equilibrium becomes unstable. By using the theory of Lasalle-Lyapunov function V, we will show the global asymptotic stability. The disease free equilibrium point is![]() .
.
Theorem
If![]() , then the disease-free equilibrium
, then the disease-free equilibrium ![]() of the system is globally asymptotically stable on
of the system is globally asymptotically stable on![]() .
.
Proof
We construct the following Lasalle-Lyapunov function ![]() on the positively invariant compact set
on the positively invariant compact set![]() . Thus on
. Thus on![]() ,
, ![]() is continuous and non negative.
is continuous and non negative.
We define
![]()
The system of ordinary differential equations given by Equation (2) can be written as
![]() (6)
(6)
This can be written as ![]() where
where
![]() and
and![]() .
.
If we define
![]()
then the derivative along the trajectories is given by ![]() as
as
![]()
We define the set![]() . The largest invariant set is contained in the set E
. The largest invariant set is contained in the set E
for which ![]() or
or ![]() or
or![]() . Thus
. Thus ![]() when
when ![]() and
and![]() . If
. If ![]() or
or ![]() and
and![]() ,
, ![]() then
then![]() . Thus by Lasalle’s invariance principle the disease free equilibrium is globally asymptotically stable on
. Thus by Lasalle’s invariance principle the disease free equilibrium is globally asymptotically stable on![]() .
.
5. The Endemic Equilibrium, EE
5.1. Local Stability of the Endemic Equilibrium, EE
Theorem
The endemic equilibrium![]() ,
, ![]() and
and ![]() is locally asymptotically stable on
is locally asymptotically stable on![]() .
.
Proof
The system of equations 5 can also be expressed as follows when we let ![]()
![]() (7)
(7)
The Jacobian computed at the endemic equilibrium using the relations given by Equation (6) can be expressed as:
![]()
To determine the stability of the endemic equilibrium![]() , we use the Routh-Hurwitz stability criteria on the characteristic equation of a third degree polynomial given by
, we use the Routh-Hurwitz stability criteria on the characteristic equation of a third degree polynomial given by![]() . We say that
. We say that ![]() is Hurwitz iff
is Hurwitz iff ![]() and
and![]() .
.
The coefficient![]() ,
, ![]() = sum of the determinants of all the principal minors of
= sum of the determinants of all the principal minors of
![]() and
and![]() .
.
The trace of J will be given as
![]()
![]()
![]() iff
iff ![]()
![]()
![]() iff
iff ![]()
To prove the Routh-Hurwitz stability criteria we compute ![]() to obtain
to obtain
![]()
![]() iff
iff
![]()
The requirements of Routh-Hurwitz stability criteria are satisfied hence this proves that the endemic equilibrium is locally asymptotically stable![]() .
.
5.2. Global Stability of the EE
Theorem
The endemic equilibrium is globally asymptotically stable on ![]() if
if![]() .
.
Proof
We will prove the global stability of the Endemic Equilibrium by using the following Lyapunov function proposed by Cai and Li (2007). Thus we have:
![]()
Then the derivative of![]() , obtained by direct calculation along the solution of
, obtained by direct calculation along the solution of ![]() is given by
is given by
![]() (8)
(8)
Substituting the expressions of the model system ![]() into the equation 7 above we get
into the equation 7 above we get
![]()
![]() can be written as
can be written as
![]() (9)
(9)
where F represents the positive terms of the equation above and G represents the negative terms of the said equation. The expression of F and G are as follows:
![]()
![]()
Thus from equation 8 if ![]() then we obtain that
then we obtain that![]() . We have that
. We have that ![]() if and only if
if and only if![]() ,
, ![]() and
and![]() .
.
We define the set![]() . Therefore the largest compact invariant set is the singleton
. Therefore the largest compact invariant set is the singleton
set ![]() which is the endemic equilibrium. By Lasalle Invariance principle
which is the endemic equilibrium. By Lasalle Invariance principle ![]() is globally asymptotically stable on
is globally asymptotically stable on![]() .
.
NB: In an upcoming article, we include a human protection factor and the development of mosquito resistance during their life time. Wa also allow some resistant vectors to become sensitive to insecticides.
6. Conclusion
In this study, we formulated a malaria model representing the transmission of malaria by two types of vectors; the traditional mosquito which is sensitive to insecticides in ITNS and IRS, and a resistant type which is able to survive despite the control measures aimed at shortening their life span and limiting the biting rate. The basic reproduction number is determined as a contribution of the two types of vectors. The model is shown to be positively invariant, hence well posed. The Disease Free Equilibrium and the Endemic equilibrium are shown to be locally and globally asymptotically stable when ![]() and
and![]() , respectively. The development of resistance in sensitive mosquitoes and the loss of resistance in resistant mosquitoes will be done in an upcoming article.
, respectively. The development of resistance in sensitive mosquitoes and the loss of resistance in resistant mosquitoes will be done in an upcoming article.
Acknowledgements
We wish to thank Calistus Ngonghala for the contribution and advise he gave during the formulation of this model.