Cryptographic Schemes Based on Elliptic Curves over the Ring Zp[i] ()

Received 9 January 2016; accepted 26 February 2016; published 29 February 2016

1. Introduction
Elliptic curve cryptography has been an active area of research since 1985 when Koblitz (Ref. [1] ) and Miller (Ref. [2] ) independently suggested using elliptic curves for public-key cryptography. A lot of work has been done on elliptic curve cryptography (Ref. [3] -[7] ). Because elliptic curve cryptography offers the same level of security as compared to RSA with considerably shorter keys, it has replaced traditional public key cryptosystems, especially, in environments where short keys are important. Public-key cryptosystems are computationally demanding and, hence, the fact that elliptic curve cryptography has been shown to be faster than traditional public-key cryptosystems is of great importance. Elliptic Curve Cryptographic (ECC) schemes are public-key mechanisms that provide the same functionality as RSA schemes. However, their security is based on the hardness of a different problem, namely the Elliptic Curve Discrete Logarithmic Problem (ECDLP). Most of the products and standards that use public-key cryptography for encryption and digital signatures use RSA schemes. The competing system to RSA is an elliptic curve cryptography. The principal attraction of elliptic curve cryptography compared to RSA is that it offers equal security for a smaller key-size.
2. Auxiliary Result
In this section first we discuss some essential arithmetic of elliptic curves, and then we mention some auxiliary results which are necessary to prove the main result. Although a lot of literature exist on arithmetic of elliptic curves (Ref. [8] -[11] ), a simple and easier arithmetic of elliptic curves are given by the following (Ref. [10] ):
An elliptic curve 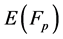 over a finite field
over a finite field 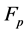 is defined by the parameters
is defined by the parameters  (a and b satisfy the relation
(a and b satisfy the relation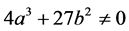 ), consists of the set of points
), consists of the set of points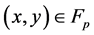 , satisfying the equation
, satisfying the equation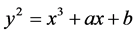 . The set of points on
. The set of points on  also include point O, which is the point at infinity and which is the identity element under addition. Actually elliptic curve are not ellipse. They are so called because they are described by cubic equation similar to those are used for calculating the circumference of an ellipse.
also include point O, which is the point at infinity and which is the identity element under addition. Actually elliptic curve are not ellipse. They are so called because they are described by cubic equation similar to those are used for calculating the circumference of an ellipse.
The Addition operation is defined over ![]() and it can be seen that
and it can be seen that ![]() forms an abelian group under addition.
forms an abelian group under addition.
![]() .
.
If![]() , then
, then![]() . (The point
. (The point ![]() and is called the negative of P and is denoted
and is called the negative of P and is denoted![]() ).
).
If ![]() and
and ![]() and
and![]() , then
, then![]() , where
, where
![]() , and
, and![]() .
.
Let![]() . Then the point
. Then the point![]() ,
,
where![]() , and
, and![]() .
.
Now we discuss the auxiliary result of this section. For a prime number p, let ![]() where
where![]() , be a ring having
, be a ring having ![]() elements. Then we have the following assertion:
elements. Then we have the following assertion:
Lemma 2.1. (Ref. [12] ) An element ![]() is invertible in
is invertible in ![]() if only if
if only if![]() .
.
Proof. Let ![]() be invertible then there exists an element
be invertible then there exists an element ![]() in
in ![]() such that
such that
![]() (1)
(1)
which implies ![]() i.e.
i.e. ![]() and
and![]() .
.
In (1) take the conjugate
![]() (2)
(2)
Multiply (1) and (2), we get
![]()
We deduce
![]() , so
, so![]() .
.
Lemma 2.2. (Ref. [13] [14] ) Let p be a prime number. Then ![]() is field iff
is field iff![]() .
.
Proof. Assume that ![]() is not field if
is not field if ![]() then
then ![]() an element
an element![]() , which is not
, which is not
invertible. By Lemma 2.1, we have![]() . So
. So![]() , where
, where![]() . We can write
. We can write![]() ,
,
![]() with
with![]() . Suppose a is not divisible by p then p does not divide t but p divides
. Suppose a is not divisible by p then p does not divide t but p divides![]() . Using proposition 1.2 [3] , we obtain
. Using proposition 1.2 [3] , we obtain![]() . We have
. We have![]() . Supposing
. Supposing![]() , we can write
, we can write ![]() then
then ![]() is not invertible. Assume
is not invertible. Assume![]() , then
, then ![]() an element
an element ![]() such that
such that
![]() because
because ![]() this implies that
this implies that ![]() and hence
and hence![]() . So
. So![]() .
.
We deduce that ![]() is not invertible. This completes the proof of the result.
is not invertible. This completes the proof of the result.
Theorem 2.3. For two isomorphic abelian groups ![]() and
and ![]() with the same unit element e, let
with the same unit element e, let ![]() and also let
and also let ![]() be a mapping defined by
be a mapping defined by
![]()
such that
![]()
where f is the isomorphism between ![]() and
and![]() . Then
. Then ![]() is an internal composition law, commutative with
is an internal composition law, commutative with
identity element e and all elements in E are invertible.
Proof. It is clear that ![]() is an internal composition law over E.
is an internal composition law over E.
To show that e is the identity element with respect to binary operation![]() .
.
Let x in E. If ![]() then
then
![]()
because ![]() and e is the unit element of
and e is the unit element of![]() .
.
Else![]() , then
, then
![]()
because ![]() and e is unit element of
and e is unit element of![]() .
.
![]() is commutative
is commutative
We have ![]() and
and ![]() two abelian groups with the same unit element e.
two abelian groups with the same unit element e.
Let![]() . If
. If ![]() then
then
![]()
If ![]() then
then
![]()
If ![]() then
then
![]()
If ![]() then
then
![]() .
.
3. Elliptic Curve over the Field ![]()
Let ![]() be two elliptic curve over the field
be two elliptic curve over the field![]() , where p is a prime number such that
, where p is a prime number such that![]() , defined by
, defined by
![]() and
and ![]()
where O is the point at infinity.
Corollary 3.1. If ![]() then
then![]() .
.
Proof. Let![]() , then
, then
![]() and
and ![]()
This implies that
![]() i.e.
i.e. ![]()
which is a contradiction.
Hence
![]() .
.
4. Main Result
Theorem 4.1. Let f be a mapping from ![]() to
to ![]() defined by
defined by
![]() and
and ![]()
Then f is a bijection.
Proof. First we show that f is well defined.
Let ![]() then
then![]() , then
, then ![]() i.e.
i.e. ![]() therefore
therefore ![]()
Hence f is well defined.
f is one-one. Let ![]() such that
such that
![]()
![]()
This implies that ![]() i.e.
i.e. ![]()
So, ![]()
Hence, f is one-one.
f is onto. Let![]() . Then
. Then ![]() or
or ![]()
This implies that ![]() because
because ![]() and
and ![]()
Thus, f is onto.
f is homomorphism. Let ![]() there is three cases arise:
there is three cases arise:
Case I. When ![]()
As we know that addition of two different points ![]() and
and ![]() on elliptic curve is given by
on elliptic curve is given by
![]()
where ![]() and
and ![]()
So we have
![]()
where ![]() and
and ![]()
Again
![]()
where ![]() and
and![]() .
.
It is obvious that ![]() this implies that
this implies that ![]() and
and![]() .
.
Therefore
![]() .
.
Case II. When ![]() and
and ![]()
![]()
where ![]() and
and![]() .
.
Again
![]()
where ![]() and
and![]() .
.
It is evident that ![]() then,
then, ![]() and
and![]() .
.
Therefore,
![]()
Case III. When ![]() and
and ![]()
We have
![]()
and
![]()
Thus
![]()
Therefore, in either case f is an homomorphism. Hence f is a bijection.
Corollary 4.2. For two isomorphic abelian groups ![]() and
and ![]() with the same unit element O, let
with the same unit element O, let ![]() and also let
and also let ![]() be a mapping defined by
be a mapping defined by
![]()
such that
![]()
where f is the isomorphism between ![]() and
and![]() . Then
. Then ![]() is an internal composition law, commutative with identity element O and all elements in E are invertible.
is an internal composition law, commutative with identity element O and all elements in E are invertible.
Proof. Keeping in view the result of theorem-2.3, corollary-2.4, and theorem-3.1, it is evident that ![]() is an internal composition law, commutative with identity element O and all elements in E are invertible.
is an internal composition law, commutative with identity element O and all elements in E are invertible.
Proof. Since ![]() is isomorphic to
is isomorphic to ![]() this implies
this implies ![]()
Now,
![]()
This implies that
![]()
Therefore,
![]() .
.
5. Cryptographic Applications
In this section we shall illustrate our proposed methods for coding of points on Elliptic Curve, then exchange of secret key and finally use them for encryption/decryption.
5.1. Coding of Element on Elliptic Curve
It is described with the help of illustration 5.1 and illustration 5.2.
Illustration 5.1. For ![]() and
and![]() , Then codes of elements of
, Then codes of elements of ![]() are given by
are given by
![]()
Since, ![]() and
and ![]()
Therefore
![]() .
.
and
![]() .
.
Coding of element ![]() are described as follow
are described as follow
Let![]() , where
, where ![]() for j = 0 or 1 and z = 0 or 1. Then coding method is given by
for j = 0 or 1 and z = 0 or 1. Then coding method is given by ![]() which produces the following codes
which produces the following codes
![]()
Illustration 5.2. For ![]() and
and![]() . The coding of points of
. The coding of points of ![]() can be described as
can be described as
![]()
![]()
Let![]() , where
, where ![]() for j = 0 or 1 and z = 0 or 1. Then coding method is given by
for j = 0 or 1 and z = 0 or 1. Then coding method is given by ![]() which produces the following codes
which produces the following codes
![]()
The above scheme helps us to encrypt and decrypt any message of any length.
5.2. Exchange of Secret Key
1) For a publically integer p, and an elliptic curve ![]() let
let ![]() of order n.
of order n.
2) P generates a subgroup say ![]() which is used to encrypt the message m.
which is used to encrypt the message m.
Now, key exchange between Alice and Bob can be described as follows
3) Alice chooses a random number![]() , computes
, computes ![]() and sends it to Bob.
and sends it to Bob.
4) Bob chooses a random number![]() , computes
, computes ![]() and sends it to Alice.
and sends it to Alice.
5) Alice computes![]() .
.
6) Bob computes![]() .
.
7) Alice and Bob are agree with a point![]() ,choose the binary code of point S as a private key, which transformed on the decimal code
,choose the binary code of point S as a private key, which transformed on the decimal code![]() .
.
Remark. With the secret key ![]() such as the decimal code of point S Alice and Bob can encrypt and decrypt the message (m).
such as the decimal code of point S Alice and Bob can encrypt and decrypt the message (m).
Illustration 5.3. Let ![]() and
and ![]()
are two elliptic curve defined over the same field ![]() having
having ![]() element, where 8831 be a prime number such that
element, where 8831 be a prime number such that ![]() and a point
and a point ![]() of order 4427.
of order 4427.
1) Alice chooses a random number![]() , compute
, compute ![]() and sends it to Bob.
and sends it to Bob.
2) Bob chooses a random number ![]() and compute
and compute ![]() and sends to it Alice.
and sends to it Alice.
3) Alice computes![]() .
.
4) Bob computes![]() .
.
5) Alice and Bob are agree with a point![]() , choose the binary code of point S as a private key, which transformed on the decimal code
, choose the binary code of point S as a private key, which transformed on the decimal code![]() .
.
5.3. ECC Key Generation Phase
Now, exchange of secret key involves the following steps:
1) Encode the message m on the point![]() .
.
2) Choose a random number k, compute ![]() and calculate
and calculate![]() .
.
3) Public key is![]() .
.
4) Private key is![]() .
.
5.4. ECC Encryption Phase
To encrypt![]() , a user choose an integer
, a user choose an integer ![]() at random and sends the point
at random and sends the point![]() . This operation is shown in Figure 1.
. This operation is shown in Figure 1.
5.5. ECC Decryption Phase
Decryption of the message ![]() is done by multiplying the first component
is done by multiplying the first component ![]() of the received point
of the received point ![]() and the secret key
and the secret key![]() , and the result is subtracted from the second component
, and the result is subtracted from the second component ![]() i.e.:
i.e.:
![]()
This operation is shown in Figure 2.
Illustration 5.4. The![]() and
and![]()
are two elliptic curves defined over the same field ![]() having
having ![]() element where 8831 be a prime number such that
element where 8831 be a prime number such that ![]() and a point
and a point ![]() of order 4427.
of order 4427.
Alice’s message is the point![]() .
.
Bob has chosen his secret random number ![]() and computed
and computed
![]()
and calculated
![]()
Bob publishes the point. Alice chooses the random number ![]() and computes
and computes
![]()
and
![]()
Alice sends (7966,6354) and (5011,2629) to Bob, who multiplies the first of these point by
![]() .
.
Bob then subtracts the result from the last point that Alice sends him. Note that he subtracts by adding the point with the second coordinate negated:
![]()
Bob has therefore received Alice’s message.
Acknowledgements
This research work is supported by University Grant commission (UGC) New Delhi, India under the Junior Research Fellowship student scheme..