Piketty’s Capital-Income Theory Reconsidered for a Small Open Economy with Increasing Savings Rate ()
Received 13 November 2015; accepted 11 February 2016; published 14 February 2016

1. Introduction
Researches on national accounting system have entered a new phase since Piketty and his coauthors offered a sweeping new view of capital/income ratio, that is, the capital/income ratio increases if rate of return on capital (r) is greater than economic growth rate (g) (Atkinson, Piketty and Saez (2011) [1] , Alvaredo, Atkinson, Piketty and Saez (2013) [2] , Piketty (2011, 2014, 2015) [3] -[5] , Piketty and Saez (2003, 2014) [6] [7] , Piketty and Zucman (2014) [8] etc.). Since then, numerous attempts have been made to examine the relationship between return on capital, economic growth and the capital/income ratio.
Rowthorn (2014) [9] investigates, based on a CES (constant elasticity of substitution) production function, if capital accumulation increases the capital/income ratio, while Bernardo, Martínez and Stockhammer (2014) [10] , constructing a post Keynesian model, analyze if r > g is necessarily associated with increase in the capital/in- come ratio. Dumenil and Levy (2014) [11] , focusing on fixed capital, examine if the capital/income ratio has a tendency to increase in the capitalist economy.
Mankiw (2015) [12] also recalibrates Piketty’s logic taking into account consumption, procreation and taxation, to show that Piketty’s scenario is far from what we have experienced. That is, according to Mankiw (2015) [12] , rate of return on capital (r) needs to exceed economic growth rate (g) by at least 7 percentage points per year in order to have the worrisome endless inegalitarian spiral where wealth of capitalist class grows faster than income of workers to increase the capital/income ratio. Fujita (2015) [13] reveals the condition where r > g increases the capital/income ratio, by laying out a theoretical model that distinguishes real capital and financial one.
The present paper, in the spirit of these studies, attempts to shed new light on the aspects that are missed in the research on the capital/income ratio. More precisely, following the recent literatures that pay attention to the dynamics of the external balance sheets of countries (Lane and Milesi-Ferretti (2007) [14] , Gourinchas and Rey (2007) [15] , Zucman (2013) [16] , Piketty and Zucman (2014) [8] etc.), we construct a small open economy model where savings rate increases gradually from negative value, to examine if Piketty’s results for large countries are robust for such a country.
Analysis of the present paper demonstrates that Kuznets curve (a hump-shaped trajectory ontime-capital/ income ratiospace, shown by Kuznets (1955) [17] ), which Piketty (2014) [4] thinks to apply only to the early 1950s, is drawn for a small open country whose savings rate increases gradually from negative value. It is also revealed that the capital/income ratio decreases in such a country if (1) the savings rate increases or (2) the return on capital increases.
2. Basic Model
Let us consider a small open country that takes the world rate of return on capital as given. Following Piketty and Zucman (2014) [8] , we assume that the world rate of return on capital is constant over time at r. We also assume, as in Piketty and Zucman (2014) [8] , national wealth in period t, W(t), is decomposed into domestic capital in period t, K(t), and net foreign assets in period t, F(t), as
 (1)
(1)
whose accumulation dynamics is
 (2)
(2)
where S(t) is the saving in period t.
With reference to national income also, as in Piketty and Zucman (2014) [8] , we formulate the national income in period t, Y(t), to be the sum of domestic output in period t, YD(t), and income from the net foreign assets in period t, rF(t). That is to say, 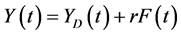 , which is rewritten as
, which is rewritten as
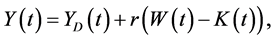 (3)
(3)
by making use of (1). YD(t) is assumed to be produced by a Cobb-Douglas function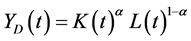 , where L(t) is the labor input in period t and α is a parameter that satisfies 0 < α < 1.
, where L(t) is the labor input in period t and α is a parameter that satisfies 0 < α < 1.
If we normalize the labor to be unity for the simplicity of analysis, and assume the capital receives its marginal product (i.e.,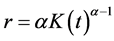 ) as in Piketty and Zucman (2014) [8] etc., we have the optimal amounts of capital and domestic output in period t, respectively, as
) as in Piketty and Zucman (2014) [8] etc., we have the optimal amounts of capital and domestic output in period t, respectively, as
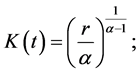 (4)
(4)
 (5)
(5)
Note that in the setting of the present paper, the optimal amounts of capital and domestic output remain constant over time. Thus, we can say that results of the present paper are virtually the same as those derived by assuming that capital and domestic output are already at their optimal levels.
By substituting (4) and (5) into (3), we have the national income in period t, Y(t), as
 (6)
(6)
If we assume that a fraction s(t) of the national income is saved in period t and make use of (2), we obtain the wealth accumulation dynamics as
 (7)
(7)
which reduces to the following derivative of W with respect to time t
 (8)
(8)
assuming continuous time horizon in order to simplify the analysis.
3. Dynamics of the Ratio of Capital to Income
Differentiating (6) and substituting (8) into it, we have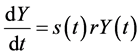 , with which we have the economic growth rate
, with which we have the economic growth rate 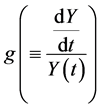 as
as
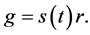 (9)
(9)
Since s(t) < 1, it follows that r is greater than g (i.e., r > g), the inequality Piketty (2014) [4] etc. demonstrated to be seen almost always in history.
Now, if we let β(t) denote the capital/income ratio in period t (i.e., ), we have its derivative with respect to t as
), we have its derivative with respect to t as
![]() (10)
(10)
Since ![]() from (8),
from (8), ![]() by definition and
by definition and ![]() from (9), we have
from (9), we have
![]() . (11)
. (11)
In the following, in order to obtain a concrete solution, we assume s(t) to be a linear function of t, i.e., ![]() , where θ is a positive parameter that is sufficiently small so as to keep s(t) less than unity, and η is also a positive parameter. We also assume that negative saving (i.e. s < 0) is possible, based on the evidence that low income countries often suffer from negative saving (World Bank (2015) [18] for example) and the theories that demonstrate low income leads to negative saving (permanent income hypothesis (Friedman (1956) [19] )) for example).
, where θ is a positive parameter that is sufficiently small so as to keep s(t) less than unity, and η is also a positive parameter. We also assume that negative saving (i.e. s < 0) is possible, based on the evidence that low income countries often suffer from negative saving (World Bank (2015) [18] for example) and the theories that demonstrate low income leads to negative saving (permanent income hypothesis (Friedman (1956) [19] )) for example).
If we insert ![]() into (11), the differential equation reduces to
into (11), the differential equation reduces to
![]() , (12)
, (12)
which is solved as
![]() (C is a constant of integration) (13)
(C is a constant of integration) (13)
by noting that θ, η and r are exogenous variables, setting ![]() and using separation of variables method.
and using separation of variables method.
Now, let us specify C = 1, so that we have
![]() , (14)
, (14)
by assuming the initial conditions to be ![]() and
and![]() . Note that even if C ≠ 1, the result remains intact as long as C > 0, which is an implicit assumption to keep β(t) positive.
. Note that even if C ≠ 1, the result remains intact as long as C > 0, which is an implicit assumption to keep β(t) positive.
Graph of (14) is depicted ont-β space as a hump-shaped trajectory as in Figure 1, whose implication is that as an economy develops, the capital/income ratio first increases and then decreases, which Piketty (2014) [4] interprets to mean the inequality first increases and then decreases. Thus, we obtain the following proposition.
Proposition:
Capital/income ratio β(t) first increases and then decreases as time goes by in a country that takes the constant world rate of return on capital as given and whose savings rate increases gradually from negative value.
This proposition is what Kuznets curve implies. So that, we can say from this proposition that Kuznets curve, which Piketty (2014) [4] thought to apply only to the early 1950s for large countries, is drawn for a small open country that suffers from negative saving in the early phase of its development. Since r > g always holds in this model, we can go so far as to say Kuznets curve is drawn even if r > g holds for a small open country.
By making use of Equation (14), we can also show the effect of the change in exogenous variables to the shape of Kuznets curve. That is to say, the curve shifts inwards as in Figure 2 if parameter θ increases (which means increase in the savings rate) or the rate of return on capital r increases.
Thus, we have the following corollary.
Corollary:
Capital/income ratio β decreases if (1) the savings rate increases or (2) the return on capital increases, in a country that takes the constant world rate of return on capital as given and whose savings rate increases gradually from negative value.
![]()
Figure 1. Changes of capital/income ratio β(t).
![]()
Figure 2. Effect of an increase in the savings rate or the return on capital.
Corollary (1) is in sharp contrast to Piketty’s Second Law of Capitalismin Piketty (2014), ![]() , which
, which
means that a rise in the savings rate s increases β. Corollary (2) also contrasts to Piketty (2014) [4] etc., which conclude that a rise in r increases β. Since Piketty (2014) [4] assumes large countries, we can say from this Corollary that what applies for large countries doesn’t apply for small countries.
4. Conclusions
In the present paper, we investigate if Piketty’s results for large countries are robust for a country that takes the world rate of return on capital as given and whose savings rate increases gradually from negative value. The main findings of this extended Piketty’s model are: for such a country, (1) Kuznets curve is drawn and (2) capital/income ratio decreases in accordance with a rise in the savings rate and the return on capital, all of which are in sharp contrast to Piketty’s results for large countries, although the framework of this paper is basically the same as that of Piketty’s. From these results, we can say that what applications for large countries don’t apply for small countries.
In the setting of the present paper, capital and domestic output are constant over time, and hence, the engine of the economic growth is the foreign direct investment. This kind of modeling may be justified for a developing country where capital and domestic output reach their optimal levels quickly since each level is not so large. However, it remains to be seen if the results of the present paper are robust when it takes time for them to reach their optimal levels so as to necessitate formulating the process of capital accumulation. We take up such analysis next.