A Note on Cochran Test for Homogeneity in Two Ways ANOVA and Meta-Analysis ()
Received 24 August 2015; accepted 27 December 2015; published 30 December 2015
1. Introduction
In ANOVA methodology, it is generally accepted that the error variance is unknown and is the subject of an estimate. However, in practice, these fundamental assumptions are rarely checked, forcing the use of Fisher statistic in the homogeneity test on the mean of the different groups ([1] -[5] ).
According to the work of [6] , the statistic test of homogeneity of two ways is of the form:
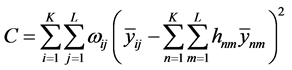(1)
where 
, 
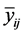and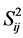 
are respectively the mean and variance sample of the group (i, j) consisting of 
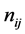observations;
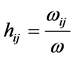, with
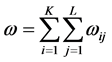. In the foregoing expression, the number of groups is equal to KL, and Equation (1) is valid if
.
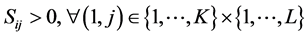[7] tests the homogeneity of medical treatment between both groups of patients, using the [6] statistic in a meta-analysis (e.g. see [1] ). The above studies suggest that under the null hypothesis H0 of equality of the means of different groups (i, j), the Cochran statistic asymptotically follows a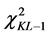
. However, neither the work of [6] , nor those of [7] offer a formal proof of this result.
Despite the existence of some attempts proposed by [8] -[10] and [11] , in the literature, the construction of homogeneity statistical test on mean (or medians and percentiles) of various groups is generally based on a three-step methodology.
Step 1: The global average is estimated by a linear combination of the individual averages.
, where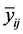 
represents respectively the mean and the non-negative weight of group
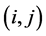, and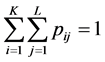
.
Step 2: One assumes that the population variances of each group are unknown and estimated by the variances of the corresponding samples.
Let the vector q be given by: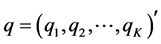 
where,
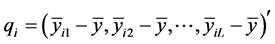. We have:
![]()
;
![]()
, with![]()
, ![]()
The covariance matrix is then estimated by![]()
, with
![]()
Step 3: One constructs the statistics test
![]()
In explicit form,
![]()
where ![]()
is the Moore-Penrose inverse matrix ![]()
of![]()
.
In the case of one way ANOVA, [12] provides a faster method of building statistics homogeneity test, showing that this statistic is equivalent to Cochran. However, the authors offer no generalization of their result to the case of the two-factor ANOVA.
Following [12] , this paper proposes to generalize the construction of the statistical homogeneity test in ANOVA two ways settings. To our knowledge, this issue has not been discussed in the literature. Beyond the theoretical importance, in practice it induces many applications, particularly in medicine, to compare the effectiveness of two methods of administration of a molecule to two different populations.
The remainder of the paper is organized as follows: Section 2 presents the main results. Section 3 provides an empirical evaluation of the proposed test; and Section 4 concludes the paper.
2. Main Results
In this section, we first show that statistics ![]()
(see Equation (3) below) is asymptotically distributed according to a![]()
. Then, we prove that the Cochran statistics in a two ways ANOVA is equivalent to T. Finally, we conclude that the C statistics also follows a ![]()
distribution . We thus have the following important results.
Proposition 1.
![]()
(2)
Proof.
We suppose that ![]()
for the groups ![]()
where the variance of the population ![]()
is unknown.
Now let us consider![]()
, then![]()
, ![]()
and![]()
; with![]()
.
Let us consider![]()
, the variance? covariance matrix of d is written as follows:
![]()
According to [13] , p.9, Theorem 1.7, the inverse of ![]()
exists and it is given by:
![]()
,
where![]()
. Therefore, one obtains the result. +
Proposition 2.
![]()
(3)
Proof.
In practice, the variance ![]()
is unknown and estimated from the variance of the sample![]()
. Replacing in Equation (2) ![]()
by![]()
, and since,
![]()
Based on Slutsky Theorem, the statistic T is asymptotically distributed as a ![]()
distribution. +
Proposition 3.
T and C are equivalent.
Proof.
Since,
![]()
![]()
![]()
and since,
![]()
We obtain:
![]()
Therefore, we get:
![]()
Also since, ![]()
, i.e.
So that,
![]()
Therefore we obtain the equivalence between T and C. And as it was demonstrated that T is asymptotically distributed as a![]()
, then C also follows the same law. +
Defining G by
![]()
![]()
(4)
G verifies the following invariance property.
Theorem 1.
The G statistics is invariant by the choice of the weights and![]()
.
Proof of Theorem 1.
To prove this theorem, we need the following lemmas.
Lemma 1.
According to [14] , p. 130, 7.11 (d) (ii), ![]()
is invariant, where ![]()
is the generalized inverse matrix of ![]()
and ![]()
is the inverse M-P matrix of X. Therefore,![]()
.
Proof.
Straightforward. +
Lemma 2.
According to [14] p. 144, 7.73, if A and B are compatible matrices, then![]()
.
Proof.
Straightforward. +
Lemma 3.
For Q in (4), its singular value decomposition is, ![]()
, where ![]()
and the k-th column of V is ![]()
Proof.
It is easy to show that
![]()
where ![]()
is the identity matrix of dimension ![]()
and ![]()
is the squared matrix of dimension ![]()
whose elements are 1. The eigenvalues of ![]()
are
![]()
.
Therefore, ![]()
and the k-th column of V is![]()
. +
Lemma 4.
We have ![]()
Proof.
According to Lemma 3, ![]()
, where![]()
. Therefore, ![]()
+
From the above lemmas, we then can provide the proof of Theorem 1.
Proof of Theorem 1.
![]()
Therefore, ![]()
is invariant for Q and ![]()
. As![]()
, one obtains ![]()
. In other words, the G statistics is determined by the variance and means of the sample in C. Finally, G is independent of the weights ![]()
and Q. +
3. Application Meta-Analysis
In this Section, we empirically verify equality between both statistics G and C from a meta-analysis. The data come from the Stael program base. Specifically, we want to compare the effectiveness of three different molecules and, at the same time, we want to appreciate the impact of administration mode of different molecules (orally or intravenously). However, we don’t want to multiply experiments and number of subjects. In total, there are six possible combinations that means 6 series of measures (of different or identical subjects) on which is then measured a relevant quantitative parameter, sensible capture the influence of the decision of the molecules tested). The various combinations of two factors (molecules 3 and 2 modes of treatment) are the factorial design. Here the factor 1 has 3 modes: molecule A, B and C, while the factor 2 admits 2 modalities: Oral and injection.
Table 1 summarizes the distribution of the data used.
Table 2 and Table 3 report the main statistical characteristics of the both factors.
Table 4 gives the estimation of different parameters and that of the Cochran statistic.
Thus, from the definition of Cochran statistics C:
![]()
with K = 3 and L = 2. After calculation, one obtains: C = 44.5
![]()
Table 4. Estimation of main parameters.
Then we determine the G statistics as:
![]()
![]()
![]()
The Moore-Penrose decomposition ![]()
of the matrix ![]()
in pseudo-inverse is obtained by using Matlab program. Thus we get the singular decomposition matrix that provides a diagonal matrix (with positive values), and matrices ![]()
such that![]()
. We obtains
![]()
![]()
;
![]()
Finally, we have![]()
. To obtain![]()
, we simply reverse the elements on the diagonal excepted those equal to zero. Thus,
![]()
The Moore-Penrose pseudo-inverse matrix of ![]()
is then given by,
![]()
Therefore, the G statistics is calculated according to the formula, ![]()
where ![]()
; we get![]()
.
Finally, we can verify the invariance property of G statistics, compared to ![]()
weights. It is assumed in this case that the weights are identical in all groups![]()
, that means that
![]()
.
We then obtain
![]()
![]()
Returning to the procedure described in the previous Section, the following results were obtained, ![]()
and
![]()
And the corresponding Moore-Penrose matrix is
![]()
Once again, we can observe that
![]()
Interpretation
According to the above results, we observe that![]()
, and G is invariant whatever the choice of weights is. Finally, the null hypothesis H0 that assume that all groups ![]()
have the same mean, can be tested based on the fact that ![]()
. The tabulated statistics at the 5% level is 11.070. As a![]()
, the null hypothesis H0 of homogeneity between groups is rejected.
4. Final Remarks
The literature generally uses a multi-step method for determining homogeneity statistics test. It is based on a linear combination of individual mean of the sample to estimate the overall mean. Like the G statistic in (6), this approach involves determining a covariance matrix and its Moore-Penrose inverse. However, we show that Theorem 1 generalizes the result of [12] in a two ways ANOVA and simplifies this process. We build a G statistic that is equivalent to C. In other words, the expression of C provides a simple formula for determining the statistic in the homogeneity test. Moreover, Theorem 1 shows that G is asymptotically distributed according to a ![]()
distribution, and it checks certain properties of Cochran statistic. Finally, we also prove that the general form of the G statistic is invariant regardless of the choice of weights.