Shrinkage Estimation of Semiparametric Model with Missing Responses for Cluster Data ()
Received 23 September 2015; accepted 21 December 2015; published 24 December 2015

1. Introduction
In real application, the analysis of cluster data arises in various research areas such as biomedicine and so on. Without loss of generality, the data are clustered into classes in terms of the objects which have certain similar property. For example, focus on the same confidence interval as a cluster. Numerous parametric approaches are applied to the analysis of cluster data, and with the rapid development of computing techniques, nonparametric and semiparametric approaches have attained more and more interest. See the work of Sun et al. [1] , Cai [2] , Vichi [3] , Yi et al. [4] , Carrol [5] , and He [6] , among others.
Consider the semiparametric partially linear varying-coefficient model which is a useful extension of partially linear regression model and varying-coefficient model over all clusters, it satisfies
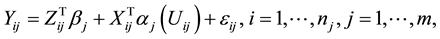 (1)
(1)
where ,
, 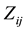 and
and 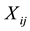 stand for the ith observation of Y, Z and X in the jth cluster.
stand for the ith observation of Y, Z and X in the jth cluster. 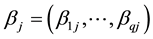 is a vector of q-dimensional unknown parametrics;
is a vector of q-dimensional unknown parametrics; 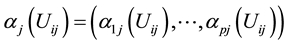 is a p-dimensional unknown coefficient vector.
is a p-dimensional unknown coefficient vector. 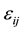 is random error with mean zero and variance
is random error with mean zero and variance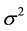 .
.
Obviously, when m = 1, model (1) reduces to semiparametric partially linear varying-coefficient model. A series of literature (You and Chen [7] , Fan and Huang [8] , Wei and Wu [9] , Zhang and Lee [10] ) have provided the corresponding statistic inference of such semiparametric model. In [8] , Fan and Huang put forward a profile least square technique and propose generalized likelihood ratio test. In [7] , You and Chen study the estimation problem when some covariates are measured with additive errors. When m = 1 and Z = 0, model (1) becomes varying-coefficient model which has been widely studied by many authors such as Fan and Zhang [11] , Hastile and Tibshirani [12] , Xia and Li [13] , Hoover et al. [14] . When m = 1, p = 1 and Z = 1, model (1) reduces to partially linear regression model which is proposed by Engle et al. [15] when they research the influence of weather on electricity demand. See the literature of Yatchew [16] , Spechman [17] and Liang et al. [18] , among others.
However, in practice, responses may often not be available completely because of various factors. For example, some sampled units are unwilling to provide the desired information, and some investigators gather incorrect information caused by careless and so on. In that case, a commonly used technique is to introduce a new variable . When
. When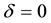 , Y represents the situation of missing, and
, Y represents the situation of missing, and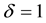 , otherwise. Suppose that responses are missing at random,
, otherwise. Suppose that responses are missing at random, 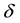 and Y are conditionally independent, then it has
and Y are conditionally independent, then it has
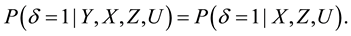
Due to the practicability of the missing responses estimation, semiparametric partially linear varying-coefficient model with missing responses has attracted many authors’ attention, such as Chu and Cheng [19] , Wei [20] , Wang et al. [21] and so on.
It is worth pointing out that there is little work concerning both missing and cluster data especially in semiparametric partially linear varying-coefficient model. If ignore the difference of clusters, it leads the predictors of response values Y far away from the true values and the estimators have poor robustness. Therefore, it is necessary to take cluster data into consideration with the purpose of improving estimation efficiency. For each cluster, introduce group lasso to semiparametric partially linear varying-coefficient model respectively on the basis of complete case data. In order to automatically select variables and conduct estimation simultaneously, lasso is a popular technique which has attracted many authors’ attention such as Tibshirani [22] , Zou [23] and so on. Due to the idea of lasso is to select individual derived input variable rather than the strength of groups of input variables, in this situation, it leads to select more factors as the approach of group lasso. As is shown in Yuan and Yi [24] , Wang and Xia [25] , Hu and xia [26] and so on. Thus, this paper centers on the technique of group lasso in a computationally efficient manner. Further then, parametric and nonparametric components are obtained by computing the weighted average per cluster. As for the inference of estimators, the properties of asymptotic normality and consistency are also provided. And Bayesian information criterion (BIC) as tuning parameter selection criterion is used in this article.
The rest of the paper is organized as follows. The use of the applied method is given in Section 2. In Section 3, the theoretical properties are provided. Conclusions are shown in Section 4. Finally, the proofs of the main results are relegated to Appendix.
2. Semiparametric Model with the Methodology
2.1. Model with Complete-Case Data
Due to there exist missing responses, for simplicity, focus on the case where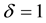 . That is so-called the method of complete case data. It is assumed that there are m independent clusters, and the number of observations in the jth cluster is
. That is so-called the method of complete case data. It is assumed that there are m independent clusters, and the number of observations in the jth cluster is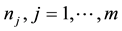 . For the ith subjects from the jth cluster, let
. For the ith subjects from the jth cluster, let
![]() be a set of random sample from model (1), then it is easy to obtain:
be a set of random sample from model (1), then it is easy to obtain:
![]() (2)
(2)
In this situation, if the parametric component ![]() is given, model (2) can be written as:
is given, model (2) can be written as:
![]() (3)
(3)
where![]() . The coefficient vector
. The coefficient vector ![]() is unknown but smooth function in u and its true value is denoted by
is unknown but smooth function in u and its true value is denoted by![]() . Suppose that the first integer
. Suppose that the first integer ![]() predictors are relevant and the rest are not.
predictors are relevant and the rest are not.
2.2. The Kernel Least Absolute Shrinkage and Selection Operator Method
Similarity, consider the jth cluster data firstly, given any index value![]() , the estimator of
, the estimator of![]() , namely
, namely![]() , can be obtained by minimizing the following locally weighted least squares function:
, can be obtained by minimizing the following locally weighted least squares function:
![]() (4)
(4)
According to![]() , define
, define ![]() and
and![]() . It is clear that,
. It is clear that, ![]() is a nature estimator for
is a nature estimator for![]() . Furthermore,
. Furthermore, ![]() is also the minimizer of the following global least squares function:
is also the minimizer of the following global least squares function:
![]() (5)
(5)
with respect to![]() . Due to Q(B) is a quadratic function in B, thus, depended on the normal equation
. Due to Q(B) is a quadratic function in B, thus, depended on the normal equation ![]() for every
for every![]() , its minimizer is obtained. From another aspect, for Q(B), as one can see,
, its minimizer is obtained. From another aspect, for Q(B), as one can see, ![]() is only involved in
is only involved in![]() ; see (4). Then it satisfies
; see (4). Then it satisfies![]() , leading to the solution
, leading to the solution![]() ; see (4). In that case,
; see (4). In that case, ![]() is also the minimizer of (5).
is also the minimizer of (5).
Due to it is assumed that the last ![]() columns of
columns of ![]() matrix should be 0. Therefore, the goal of variable selection amounts to identifying sparse columns in matrix
matrix should be 0. Therefore, the goal of variable selection amounts to identifying sparse columns in matrix![]() . In order to discriminate irrelevant variable, which implies that one should identify matrix sparse solutions in
. In order to discriminate irrelevant variable, which implies that one should identify matrix sparse solutions in ![]() in a column-wise manner. Based on the group lasso idea of Yuan and Lin [24] , Wang and Xia [26] , the penalized estimate is shown as follows:
in a column-wise manner. Based on the group lasso idea of Yuan and Lin [24] , Wang and Xia [26] , the penalized estimate is shown as follows:
![]()
where ![]() is the tuning parameter.
is the tuning parameter.
![]() (6)
(6)
![]() (7)
(7)
![]() is the kth column of B, and
is the kth column of B, and ![]() means the usual Euclidean norm.
means the usual Euclidean norm.
2.3. Local Quadratic Approximation
It is well known that, there exist many computational algorithms for the lasso-type problems such as local quadratic approximation, the least angle regression and many others. For simplicity, this article describes here an easy implementation based on the idea of the local quadratic approximation. Specifically, the implementation is based on an iterative algorithm with ![]() as the initial estimator. Let
as the initial estimator. Let
![]()
be the KLASSO estimate obtained in the mth iteration j cluster. Then, the loss function in (6) can be locally approximated by
![]()
whose minimizer is given by ![]() with the th row given by
with the th row given by
![]() (8)
(8)
where ![]() is a
is a ![]() diagonal matrix with its kth diagonal component given by
diagonal matrix with its kth diagonal component given by![]() ,
,![]() .
.
Furthermore, for each cluster and each group, by using weighted mean idea to gain the finally estimator of coefficient vector![]() . That is, the finally estimator of
. That is, the finally estimator of ![]() can be given by
can be given by
![]()
where ![]() means
means ![]() in sth cluster of ith subject.
in sth cluster of ith subject.
2.4. Estimation of Parametric Component
In terms of the above estimator of nonparametric component and according to the same criterion, the lasso estimation of parametric components ![]() are also derived. As is shown:
are also derived. As is shown:
![]() (9)
(9)
where ![]() is a coefficient vector of size q. Under its assumption, there are
is a coefficient vector of size q. Under its assumption, there are ![]() predictors relevant and the rest are not. Similarity, following the idea of local quadratic approximation and weighted mean the finally estimator of
predictors relevant and the rest are not. Similarity, following the idea of local quadratic approximation and weighted mean the finally estimator of ![]() is given by
is given by
![]() (10)
(10)
3. Theoretical Properties
3.1. Technical Conditions
The following assumptions are needed to prove the theorems for the proposed estimation methods.
Assumption 1. The random variable U has a bounded support![]() . Its density function
. Its density function ![]() is Lipschitz continuous and bounded away from 0 on its support.
is Lipschitz continuous and bounded away from 0 on its support.
Assumption 2. For each![]() ,
, ![]() is non-singular.
is non-singular.![]() ,
, ![]() and
and ![]() are all Lipschitz continuous. And they have bounded second order derivatives on [0, 1].
are all Lipschitz continuous. And they have bounded second order derivatives on [0, 1].
Assumption 3. There is an ![]() such that
such that ![]() and
and ![]() and for some
and for some ![]() such that
such that![]() .
.
Assumption 4. ![]() have continuous second derivatives in
have continuous second derivatives in![]() .
.
Assumption 5. The function K(.) is a symmetric density function with compact support.
Lemma 1. Suppose that the Assumptions of (A1)-(A5) hold, ![]() , and
, and![]() , then it satisfies
, then it satisfies
![]()
Lemma 2. If (A1)-(A5), ![]() ,
, ![]() , and
, and ![]() then
then ![]() for any
for any![]() .
.
The proof of Lemma 1 and Lemma 2 can be shown in Wang and Xia [25] .
3.2. Basic Theorems
Suppose that the Assumptions (A1)-(A5) hold. For j th cluster, let ![]()
![]() and
and ![]()
![]() Denote
Denote ![]()
![]()
Theorem 1. Assume (A1)-(A5), ![]() ,
, ![]() , and
, and![]() , then we have
, then we have ![]() for any
for any ![]()
With the purpose of considering the oracle property, define the orale estimators as follows:
![]()
Theorem 2. Suppose that the assumptions are satisfied, if![]() ,
, ![]() , and
, and![]() , then it is easy to see that
, then it is easy to see that
![]()
3.3. Tuning Parameter Selection
In the case where ![]() and
and![]() , the optimal convergence rata can be obtained and the true
, the optimal convergence rata can be obtained and the true
model can be consistently identified. Due to there exists a great challenge to select p shrinkage parameters, thus as shown in Zou [23] , wang and xia [25] , simplify the tuning parameters as follows:
![]() (11)
(11)
where ![]() is the kth column of the unpenalized estimate
is the kth column of the unpenalized estimate ![]() in jth cluster. Since
in jth cluster. Since ![]() is an estimator with
is an estimator with![]() , the results of Theorem 1 and Theorem 2 can be applied. Thus, as long as
, the results of Theorem 1 and Theorem 2 can be applied. Thus, as long as ![]() but
but![]() , one can conclude that
, one can conclude that ![]() and
and![]() . Furthermore, the original p-dimensional problem about
. Furthermore, the original p-dimensional problem about ![]() becomes a univariate problem regarding
becomes a univariate problem regarding![]() . According to BIC-type criterion,
. According to BIC-type criterion, ![]() is defined as follows:
is defined as follows:
![]() (12)
(12)
where ![]() is the number of varying coefficients identified by
is the number of varying coefficients identified by![]() .
. ![]() is
is
![]() (13)
(13)
Obviously, the effective sample size ![]() is used instead of the original sample size
is used instead of the original sample size![]() . Further then, the tuning parameter can be given by
. Further then, the tuning parameter can be given by
![]()
Note that ![]() as an arbitrary model with a total of
as an arbitrary model with a total of ![]() nonzero coefficients (i.e.
nonzero coefficients (i.e.![]() ). Then,
). Then, ![]() means the true model and
means the true model and ![]() denotes the model identified by the proposed estimate
denotes the model identified by the proposed estimate![]() . Consequently,
. Consequently, ![]() represents the model identified by
represents the model identified by![]() .
.
Theorem 3. Selection Consistency. Suppose that Assumptions (A1)-(A5) hold, the tuning parameter ![]() selected by the BIC criterion can indeed identify the true model consistency, i.e.
selected by the BIC criterion can indeed identify the true model consistency, i.e. ![]() as
as![]() .
.
4. Conclusion
In this paper, it mainly discusses the shrinkage estimation of semiparametric partially linear varying-coefficient model under the circumstance that there exist missing responses for cluster data. Combined the idea of complete-case data, this paper introduces group lasso into semiparametric model with different cluster respectively. The new method simultaneously conducts variable selection and model estimation. Meanwhile, the technique not only reduces biased results but also improves the estimation efficiency. Finally, combined the idea of weighted mean, the nonparametric and parametric estimators are derived. The BIC criterion as tuning parameter selection is well applied in this artice. Furthermore, the properties of asymptotic normality and consistency are also derived theoretically.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (61472093). This support is greatly appreciated.
Appendix
Proof of Theorem 1
Proof. Based on Lemma 2 and as shown in Hunter and Li [27] , one can know that ![]() for each
for each![]() . Then, as long as
. Then, as long as![]() , one can see that when
, one can see that when ![]() then
then ![]() converge to a positive number, otherwise,
converge to a positive number, otherwise, ![]() converge to 0. Denote
converge to 0. Denote ![]() as the upper
as the upper ![]() diagonal submatrix of
diagonal submatrix of ![]() and
and
![]() as the lower
as the lower ![]() diagonal submatrix of
diagonal submatrix of![]() . From the definition of
. From the definition of![]() , it is remarkable that each diagonal component of
, it is remarkable that each diagonal component of ![]() must converge to some finite number while
must converge to some finite number while ![]() diverge to infinity in the case where
diverge to infinity in the case where![]() .
.
For simplify, we follow (8) and ![]() can be rewritten as
can be rewritten as![]() , where
, where ![]() is a
is a ![]() block matrix given by
block matrix given by ![]() and
and ![]() with
with ![]()
![]()
![]()
![]()
![]() and
and ![]() If
If ![]() is given by
is given by ![]() one obtains
one obtains
![]()
![]()
![]()
![]()
Due to each diagonal component of ![]() must converge to some finite number while
must converge to some finite number while ![]() diverge to infinity in the case where
diverge to infinity in the case where![]() , thus each component of
, thus each component of ![]() and
and ![]() converge to 0 uniformly on [0, 1] as
converge to 0 uniformly on [0, 1] as![]() . It is easy to see that
. It is easy to see that
![]()
where![]() , and
, and ![]() are uniformly bounded. Obviously,
are uniformly bounded. Obviously, ![]() as
as ![]() when
when![]() . Therefore, sup
. Therefore, sup![]() for every
for every![]() . It completes the proof of Theorem 1.
. It completes the proof of Theorem 1.
Proof of Theorem 2
Proof. As is well known, ![]() is the solution of the following equation
is the solution of the following equation
![]()
That is to say, ![]() satisfies
satisfies
![]()
where![]() . By Lemma 2 and combined with the oracle estimator
. By Lemma 2 and combined with the oracle estimator![]() , it satisfies
, it satisfies
![]()
where ![]() with
with ![]() represents the maximal eigenvalue of an arbitrary positive definite matrix A. Notice that
represents the maximal eigenvalue of an arbitrary positive definite matrix A. Notice that ![]() as a result it completes the proof of Theorem 2. W
as a result it completes the proof of Theorem 2. W