The Evolution of Pore Water Pressure in a Saturated Soil Layer between Two Draining Zones by Analytical and Numerical Methods ()
Received 12 July 2015; accepted 7 December 2015; published 10 December 2015


1. Introduction
The study of settlements problems of structures built on compressible and saturated soils is generally performed on the basis of theory of the one-dimensional consolidation of Terzaghi [1] . The analysis of the exact solution of the fundamental equation of this theory has aroused many research works among which those of Francesco [2] have combined the solutions of D’Alembert, Fourier and Laplace equations. Work of Ndiaye [3] showed a solution of the equation by the transform of Fourier. Callaud [4] solved the problem with the transform of Laplace. The comparison of the results to those obtained previously had presented offsets.
The objective of this study is to establish analytical and numerical expressions of pore water pressures. For this we will use:
analytically separate variables method;
numerically finite element method.
We will consider a compressible saturated soil layer, comprised between two draining areas and subjected to a uniform loading. The resolution of the equation modeling the phenomenon will allow us to predict the evolution of pore water pressure in any point of the layer. For the validation of results obtained in different methods, we make the comparison of curves depending on the space and time.
2. Mathematical Modeling of the Problem
The consolidation of soils is the physical phenomenon leading to the dissipation of pore water pressure and the deformation of the solid skeleton after application of a load to the surface (see Figure 1). The study of this phenomenon is very complex especially for the compressible soils because of the low permeability and of the variation of the physical characteristics of the milieu in the course of time.
We will consider a compressible saturated soil layer, comprised between two draining areas and subjected to a uniform loading (see Figure 2). The resolution of the equation modeling the phenomenon will allow us to predict the evolution of pore water pressure in any point of the layer.
To study this problem then, they make use of simplifying assumptions. On the basis of these working hypothesis then the phenomenon studied is governed by
![]() (a) (b)
(a) (b)
Figure 1. Principle phenomenon of consolidation of saturated soils. (a) Dissipation of pore water pressure; (b) Deformation of solid skeleton.
![]()
Figure 2. Compressible and saturated layer soil comprised between two draining areas (modified from [1] ).
 (1)
(1)
With
cv: vertical coefficient of consolidation;
z: vertical space variable;
t: time.
For the unicity of the solution we will associate the Equation (1) the following conditions:
initial conditions
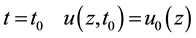 (2)
(2)
boundary conditions
 (3)
(3)
 (4)
(4)
To generalize this study and facilitate the numerical resolution, we will non-dimensional our equations through the introduction of reference variables:
vertical non-dimensional thickness
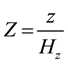 (5)
(5)
vertical non-dimensional time
 (6)
(6)
The thickness of the compressible soil layer Hz is equal to twice the distance from drainage Hd
 (7)
(7)
The previous works performed by Schiffman [5] , Legrand et al. [6] and Skempton et al. [7] showed that the factor of vertical time is given by the expression:
 (8)
(8)
Equation (1) becomes a non-dimensional relation in the following form:
 (9)
(9)
While posing
 (10)
(10)
The relation (9) becomes
 (11)
(11)
The non-dimensional initial and boundary conditions associated are:
non-dimensional initial conditions
 (12)
(12)
non-dimensional boundary conditions
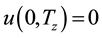 (13)
(13)
and
![]() (14)
(14)
3. Methods of Resolution
For each method of resolution, we will perform a non-dimensional transformation of the studied partial derivative equation. This will give us a non-dimensional time proportional to the vertical time factor. We will use analytically the separate variables method and numerically the finite element method.
3.1. Separated Variables Method (SVM)
The resolution of the Equation (11) by the method of the separated variables is used in several work; mention may be made the results of Braja [8] and Magnan [9] . The Equation (11) and its boundary conditions are solved by using the separated variables method. It allows obtaining an analytical solution in the form of a product of functions.
![]() (15)
(15)
While replacing (15) in (11), they obtains
![]() (16)
(16)
From where
![]() (17)
(17)
and
![]() (18)
(18)
with C a constant.
After having applied the initial and boundary conditions posed into 2, they obtain the expression of the pore water pressure in the form:
![]() (19)
(19)
with
![]() (20)
(20)
While posing
![]() (21)
(21)
From where the expression of the pore water pressure
![]() (22)
(22)
3.2. Finite Element Method (FEM)
This method of resolution is used in many studies; they can quote work of Merrien [10] , Goncalvès [11] and Dhatt et al. [12] . The finite elements used to obtain an approximate value of the solution of the Equation (11). For the resolution, we considered a linear reference element of Lagrange type. The strong variational formulation gives the following relation.
![]() (23)
(23)
The following relation being null
![]() (24)
(24)
The weak variational formulation gives the following relation
![]() (25)
(25)
The approximate value is given by the expression
![]() (26)
(26)
With
![]() : shape function.
: shape function.
The combination of the variational formulation and the shape function gives the matrices of following elementary mass and rigidity:
![]() (27)
(27)
from where the elementary mass matrix
![]() (28)
(28)
and
![]() (29)
(29)
from where the elementary rigidity matrix
![]() (30)
(30)
The assembly of the elementary matrix makes it possible to determine the solution approached to the whole domain.
![]() (31)
(31)
and
![]() (32)
(32)
The solution of the relation (11) is given in the form of an ordinary differential equation
![]() (33)
(33)
With:
![]() : global matrix of mass;
: global matrix of mass;
![]() : global matrix of rigidity.
: global matrix of rigidity.
4. Numerical Simulation and Analysis
The numerical simulation is based on the ratio of pore pressure and that of its initial value with step of regular grids. The evolution of the pore water pressure obtained by the analytical method (SVM) and numerical (FEM) are represented in the Figure 3(a) and Figure 3(b).
The graphs of the Figure 3 shows the isochrones obtained of the Figure 4.
![]() (a) (b)
(a) (b)
Figure 3. Evolution of ratio pore water pressure according to the non-dimensional variables. (a) Separated variables method; (b) Finite element method.
![]() (a) (b)
(a) (b)
Figure 4. Isochrones of ratio pore water pressure. (a) Separated variables method; (b) Finite element method.
The evolution of pore pressure depending of non-dimensional time is represented in the Figure 5.
We found that the graphs of the Figure 4 and the Figure 5 have the same allure. It appears from this observation that the evolution of pore water pressure as a function of reduced dimensions, obtained by separated variables method, are somewhat similar to those of the finite elements.
To assess the reliability of the solutions analytical and numerical we will perform a comparison.
Comparison of the Analytical and Numerical Solutions
The isochrones of pore water pressure obtained by the method of the separated variables and the finite element method are represented in the Figure 6 with Tzv = 0, Tzv = 0.01 and Tzv = 0.1.
According to the graphs of the Figure 6, we notice that the evolutions of pore water pressure almost superposed. We can note that the solutions obtained by SVM and FEM are similar for each selected time factor.
To consider error made between the two solutions exact and approached pore pressure we will carry out a comparison by linear regression (Figure 7).
We note that for each graph of the Figure 7, there is a linear relation between the values of analytical and numerical pore pressures. For each graph of the Figure 7, we obtained a linear regression line near to y = x and a coefficient of regression appreciably equal to R2 = 1. So, we can note an almost superposition of analytical and numerical isochrones.
![]() (a) (b)
(a) (b)
Figure 5. Evolution of ratio pore water pressure depending of non-dimensional time factor. (a) Separated variables method; (b) Finite element method.
![]() (a) (b) (c)
(a) (b) (c)
Figure 6. Comparison of the isochrones of pore water pressure to (a) Tzv = 0; (b) Tzv = 0.01 and (c) Tzv = 0.1.
The study of the value of pore water pressure in a compressible soil layer at each point was given. The curves obtained by of separated variables method and of finite element method are represented in the Figure 8 to Z = 0.25, Z = 0.5 and Z = 0.75.
It can note well that the evolutions of pore water pressure as a function to non-dimensional time almost superposed according to the graphs of the Figure 8. For the evaluation of the error made between the solutions exact and approached pore pressure as a function of time, we conducted a comparison of the values obtained in the graphs of Figure 9.
![]() (a) (b) (c)
(a) (b) (c)
Figure 7. Evolution of the values of numerical pore water pressure as a function to those analytical to (a) Tzv = 0; (b) Tzv = 0.01 and (c) Tzv = 0.1.
![]() (a) (b) (c)
(a) (b) (c)
Figure 8. Comparison of pore water pressure as a function of non-dimensional time to (a) Z = 0.25; (b) Z = 0.5 and (c) Z = 0.75.
![]() (a) (b) (c)
(a) (b) (c)
Figure 9. Evolution of the values of numerical pore water pressure according to those analytical for (a) Z = 0.25; (b) Z = 0.5 and (c) Z = 0.75.
We note that for each graph of the Figure 9, there is a linear relation between the values of analytical and numerical pore water pressures. For each graph of Figure 9, we obtained a linear regression line near to y = x and a coefficient of regression almost equal to R2 = 1. So, we can note an almost superposition of the analytical and numerical of curves.
5. Conclusions
This research has been enabled to study the evolution of pore water pressure in a compressible and saturated soil layer, between two draining areas subjecting a uniform loading on the surface. The non-dimensional transformation of time and thickness enabled us to understand and solve the problem.
The examination of the analytical solution is obtained by the separate variables method validated by the finite element method; let’s say that the results are satisfactory for the resolution of the problems of primary consolidation.
A comparative study by linear regression shows that the error is substantially equal to zero with a coefficient of regression close to 1. Finite element method approaches solutions of well separated variables method with respect to the equation from the primary consolidation.
We can conclude that, the solutions obtained can be used for the study of pore water pressure in compressible and saturated soil subjecting a uniform load.
Acknowledgements
I thank the authors for this work for their contributions and the Group of research of the laboratory of Mechanics and Modeling of the UFR of the engineering of the University of Thies.