On the Application of the Laplace Transform in the Study of Phillips-Type Stabilization Policy ()
Received 26 October 2015; accepted 1 December 2015; published 4 December 2015


1. Introduction
A. W. Phillips analyzed the stabilization policy for a multiplier-accelerator model [1] . Phillips’s stabilization problem is to design an endogenous policy rule capable of recovering the original equilibrium level from another equilibrium level shifted by an exogenous change of autonomous demand, while suppressing the economic fluctuations. This analysis provided the basis for subsequent advances in economic stabilization theory. It is important to reconsider the Phillips model in view of control theory because recent studies have provided analytic frameworks for economic policy by using novel control theoretical approaches [2] . Phillips defined the time lag operators in terms of a differential operator, but this operational method is not generally rigorous. In addition, the range of policy parameters to ensure the stability is not clear, because Phillips merely showed the effects of the stabilization policy with numerical examples. We therefore provide a reformulation of the Phillips model based on the Laplace transform, which is known as a rigorous justification of Heaviside’s operational calculus by Bromwich [3] , Carson [4] , and other mathematicians1. The Laplace transform has been widely used in physics and engineering, especially in classical linear control theory. The Laplace transform is a linear operator, which transforms the linear ordinary differential equation into an algebraic equation. Based on this approach, we show the effects of Phillips-type policy on equilibrium level and derive its asymptotic stability condition.
2. Laplace Transform and Transfer Function
We briefly explain the Laplace transform defined as a Riemann integral below2. Let s be a complex variable. 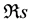 denotes the real part of s. Let
denotes the real part of s. Let 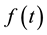 be a real-valued function of a real variable t. The Laplace transform of
be a real-valued function of a real variable t. The Laplace transform of 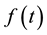 is defined by
is defined by
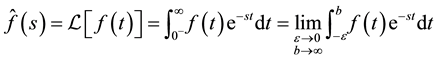 (1)
(1)
where 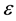 is a positive quantity.
is a positive quantity.
 is said to be of exponential order if there exist real constants M and
is said to be of exponential order if there exist real constants M and 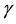 so that
so that
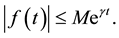 (2)
(2)
If 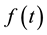 is piecewise continuous on every finite interval in
is piecewise continuous on every finite interval in 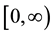 and of exponential order, then the Laplace transform exists for
and of exponential order, then the Laplace transform exists for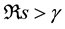 , i.e.,
, i.e.,
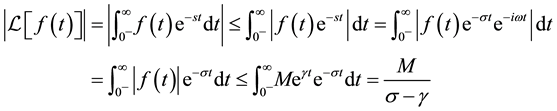 (3)
(3)
where 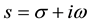 with real numbers
with real numbers . For example,
. For example,  is not of exponential order. Such functions with extremely fast growth are ignored as economic variables, but there would be no problem in practice.
is not of exponential order. Such functions with extremely fast growth are ignored as economic variables, but there would be no problem in practice.
We consider the Laplace transform of derivatives. Suppose that ![]() are continuous on
are continuous on ![]() and of exponential order and that
and of exponential order and that ![]() is piecewise continuous on
is piecewise continuous on ![]() and of exponential order. Then
and of exponential order. Then
![]() (4)
(4)
We obtain ![]() with initial condition
with initial condition![]() . Each initial value is considered as left-hand limit at the origin. Suppose that
. Each initial value is considered as left-hand limit at the origin. Suppose that ![]() exists. Consider
exists. Consider ![]() . From the left-hand side, we have
. From the left-hand side, we have
![]()
Then, it follows that
![]() (5)
(5)
with initial condition![]() . This is called the final value theorem.
. This is called the final value theorem.
Let us consider the Laplace transform of integrals. Let ![]() be piecewise continuous on
be piecewise continuous on ![]() and of exponential order. Putting
and of exponential order. Putting![]() , we have
, we have
![]() (6)
(6)
We obtain the Laplace transform of constants as follows:
![]() (7)
(7)
We define a transfer function of economic variables. Let economic variables ![]() and
and ![]() be of exponential order. Consider the following linear ordinary differential equation with constant coefficients:
be of exponential order. Consider the following linear ordinary differential equation with constant coefficients:
![]() (8)
(8)
Suppose that ![]() and
and ![]() are continuous on
are continuous on ![]() and of exponential order and that
and of exponential order and that ![]() and
and ![]() are piecewise continuous on
are piecewise continuous on ![]() and of exponential order. It follows from (4) that
and of exponential order. It follows from (4) that
![]() (9)
(9)
with initial conditions ![]() and
and![]() . The ratio of the Laplace transforms
. The ratio of the Laplace transforms ![]() is called the transfer function. We assume that all the economic variables are of exponential order and that the above continuities and initial conditions hold to obtain the form of (9).
is called the transfer function. We assume that all the economic variables are of exponential order and that the above continuities and initial conditions hold to obtain the form of (9).
3. The Model
The Phillips’s multiplier-accelerator model is described by
![]() (10)
(10)
where aggregate economic variables![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() denote demand, production, consumption, investment, autonomous demand, and government spending, respectively. These values can be negative on
denote demand, production, consumption, investment, autonomous demand, and government spending, respectively. These values can be negative on ![]() because they represent the deviations from the levels at
because they represent the deviations from the levels at![]() . l is a positive constant representing the marginal leakage. The positive constants
. l is a positive constant representing the marginal leakage. The positive constants ![]() denote the response speeds in production lag and investment lag, respectively. Since the time unit can be taken arbitrarily, we suppose
denote the response speeds in production lag and investment lag, respectively. Since the time unit can be taken arbitrarily, we suppose![]() .
.
The desired production level is taken as a reference, ![]() , and hence
, and hence ![]() denotes the deviation between current and desired level of aggregate production. We suppose that the same equilibrium level is held in
denotes the deviation between current and desired level of aggregate production. We suppose that the same equilibrium level is held in![]() , i.e.,
, i.e.,
![]() (11)
(11)
The exogenous constant deviation in autonomous demand ![]() over
over ![]() is written as
is written as
![]() (12)
(12)
where A is a bounded constant. Clearly the initial values are 0, i.e.,![]() .
.
If such an exogenous change in autonomous demand occurs, the equilibrium level of aggregate production will shift to another level, involving cyclical fluctuations. Thus, Phillips proposed a policy function ![]() for government spending as follows:
for government spending as follows:
![]() (13)
(13)
where ![]() are positive constants. The target of stabilization policy is to achieve the asymptotic stability
are positive constants. The target of stabilization policy is to achieve the asymptotic stability![]() . In this process, cyclical fluctuations are preferably suppressed.
. In this process, cyclical fluctuations are preferably suppressed.
The policy lag until demand is affected is supposed as
![]() (14)
(14)
where ![]() is a positive constant representing the response speed of policy lag.
is a positive constant representing the response speed of policy lag.
Taking the Laplace transform of (10), (13), (14), we obtain3
![]() (16)
(16)
Thus, the transfer function of ![]() and
and ![]() is given by
is given by
![]() (17)
(17)
We assumed that ![]() and
and ![]() are continuous on
are continuous on ![]() and of exponential order and that
and of exponential order and that ![]() and
and ![]() are piecewise continuous on
are piecewise continuous on ![]() and of exponential order4. Here, all the initial values are 0.
and of exponential order4. Here, all the initial values are 0.
4. Shift of Equilibrium Level
We should qualitatively verify the capability of Phillips-type policy to achieve the asymptotic stability of original equilibrium level. First, we see the effect of exogenous change in ![]() without policy.
without policy.
Theorem 1. An exogenous change in ![]() shifts the equilibrium level of production from 0 to A/l.
shifts the equilibrium level of production from 0 to A/l.
Proof. Put ![]() in (16). We have
in (16). We have
![]() (19)
(19)
Thus, it follows from (5), (7), (19) that
![]() (20)
(20)
W
Next, we analyze the effects of both the proportional and derivative policies![]() ,
,![]() .
.
Theorem 2. For![]() , the proportional policy can recover the equilibrium level to
, the proportional policy can recover the equilibrium level to![]() . The derivative policy does not affect the equilibrium level.
. The derivative policy does not affect the equilibrium level.
Proof. Put ![]() in (17). We have
in (17). We have
![]() (21)
(21)
Thus, it follows from (5), (7), (21) that
![]() (22)
(22)
The terms ![]() originate from the derivative policy. Since they converge to 0 as
originate from the derivative policy. Since they converge to 0 as![]() , the derivative policy does not affect the equilibrium level. The derivative policy is used in order only to suppress cyclical fluctuations. W
, the derivative policy does not affect the equilibrium level. The derivative policy is used in order only to suppress cyclical fluctuations. W
Finally, we confirm the asymptotic stability by using the integral policy![]() .
.
Theorem 3. For![]() , the Phillips-type policy (13) can recover the equilibrium level to 0.
, the Phillips-type policy (13) can recover the equilibrium level to 0.
Proof. It follows from (5), (7), (17) that
![]() (23)
(23)
W
5. Stability Condition
Notice that since the final value theorem can be used when ![]() exists, the time path is not ensured to be stable. Various combinations of policy parameters can be taken to achieve the stability, but the parameter constraints are not clear. We therefore focus on the condition on policy parameters to ensure the stability. As is well-known in control theory, the necessary and sufficient condition of asymptotic stability is that all roots of the denominator of transfer function have negative real parts5.
exists, the time path is not ensured to be stable. Various combinations of policy parameters can be taken to achieve the stability, but the parameter constraints are not clear. We therefore focus on the condition on policy parameters to ensure the stability. As is well-known in control theory, the necessary and sufficient condition of asymptotic stability is that all roots of the denominator of transfer function have negative real parts5.
Theorem 4. The necessary and sufficient condition for asymptotic stability of the multiplier-accelerator economy with policy (16) is as follows:
![]() (24)
(24)
and all the leading principal minors of a matrix
![]() (25)
(25)
are positive.
Proof. The Routh-Hurwitz theorem6 gives the necessary and sufficient condition for all the roots of a nth- degree polynomial
![]() (26)
(26)
with real coefficients to have negative real parts. The condition is as follows: the coefficients ![]() exist and have the same sign. In addition, all the leading principal minors of the Hurwitz matrix
exist and have the same sign. In addition, all the leading principal minors of the Hurwitz matrix
![]() (27)
(27)
are positive. We can apply the Routh-Hurwitz theorem to the denominator polynomial of (17). From definition, we obtain![]() . Similarly, the coefficients
. Similarly, the coefficients ![]() must have the same sign. Namely,
must have the same sign. Namely, ![]() and
and ![]() must be satisfied. Moreover, the matrix (25) is the corresponding Hurwitz matrix. W
must be satisfied. Moreover, the matrix (25) is the corresponding Hurwitz matrix. W
6. Conclusion
We have established a novel analytic framework on Phillips’s stabilization problem by using the Laplace transform method. On the basis of this formulation, the effects of Phillips-type policy on equilibrium level have been analyzed rigorously and qualitatively. Furthermore, we have derived the stability condition of the model by using the Hurwitz theorem. The present study has shown that the Laplace transform approach is powerful to analyze the stabilization problem. This method will give a fresh insight into the problem on stabilization policy design.
NOTES
1Some later work used the Laplace transform only to solve the differential equations of the Phillips model [5] [6] .
2See e.g., [5] [7] .
3As shown in (16), the Phillips’s notation with differential operator D is justified by the Laplace transform. For instance, Phillips wrote the production lag as
![]() (15)
(15)
4It is easy to see that (16) corresponds to the following differential equation:
![]() (18)
(18)
5See e.g., [8] .
6See e.g., [9] and mathematical appendix B in [10] .