Computer Simulation of Transition Regimes of Solitons in Stimulated Raman Scattering with Excitation of Polar Optical Phonons ()
1. Introduction
A fast progress in producing ultrashort pulses stimulates the constantly growing interest in obtaining the additional information on both the optical characteristics of matter (the longitudinal and transverse relaxation times, the constants of the transition, etc.) and the possibility of creation of super short pulses propagating in a medium without energy losses [1] [2] . One of the effects that results in solitons is SRS under the conditions of the interaction of ultrashort pulses of exciting and Stokes radiation in a medium [3] - [5] . The effect of SRS is modeled by the system of abbreviated Maxwell’s equations for the amplitudes of the electromagnetic fields and the equations of motion for the averaged polarization [6] . In many cases due to the complexity only the asymptotic behavior of those systems can be found [7] . However, to make clear, whether the SRS pulses go over to the soliton regime, it is necessary to solve the complete set of nonstationary equations which describes the temporal evolution of all interacting waves from the boundary of the medium. It is also important to consider the stability of the SRS solitons [8] . Using different numerical methods in computer simulation of space-time evolution of the interacting waves is the effective approach in analysis of the equations analytical solutions of which could not be found [9] - [11] . In this paper we use the assumption that solitons can exist if, at least, three conditions are satisfied: 1) the asymptotical solution in form of solitons is found; 2) the results of transition regime are consistent with the ones found in the previous part; 3) the obtained results are stable with respect to small (weak) perturbations. In our previous paper we established the possibility of existence of the solitons in nonstationary SRS with excitation of polar optical phonons [12] . In the present work it has been shown that the results of the computer simulation of the system of nonlinear equations (see [12] ) are consistent with the asymptotic solutions. The computer simulation was provided in Sections 3 and 4. The stability of soliton propagation was studied in Section 5.
2. Basic Equations
Let us assume that the pump laser wave with frequency  and Stokes wave
and Stokes wave  excite both the polariton radiation
excite both the polariton radiation  and the polar optical phonon
and the polar optical phonon , in the vicinity of which falls
, in the vicinity of which falls  ( the vibration
( the vibration  is supposed to be dipole-active and solitary). The two optical impulses with
is supposed to be dipole-active and solitary). The two optical impulses with  propagate in noncentrosymmetric crystal at the angles
propagate in noncentrosymmetric crystal at the angles  with respect to z-axis (perpendicular to the crystal plane). The vibration
with respect to z-axis (perpendicular to the crystal plane). The vibration , due to its combinational activity, is excited by the cubic nonlinear polarization and electric field on
, due to its combinational activity, is excited by the cubic nonlinear polarization and electric field on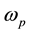 . The electric strengths are:
. The electric strengths are:
 (1)
(1)
 (2)
(2)
where: 
 are the wave vectors in linear theory;
are the wave vectors in linear theory;  are the unit vectors ( we assume that only waves of certain fixed polarization are effectively involved into interaction);
are the unit vectors ( we assume that only waves of certain fixed polarization are effectively involved into interaction); 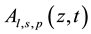 are the amplitudes of interacting waves. The phonon vibration is:
are the amplitudes of interacting waves. The phonon vibration is:
![]() (3)
(3)
where ![]() is collinear with
is collinear with![]() . We neglect the pumping of energy into the anti-Stokes and higher Stokes components, since we consider the case in which the intense fields of the exciting (laser) and first Stokes waves are present at the input of the medium. The basic system of nonlinear equations was found in [7] (the first three equations are abbreviated Maxwell’s whereas the fourth one is the equation that simulates the behavior of the nonlinear medium):
. We neglect the pumping of energy into the anti-Stokes and higher Stokes components, since we consider the case in which the intense fields of the exciting (laser) and first Stokes waves are present at the input of the medium. The basic system of nonlinear equations was found in [7] (the first three equations are abbreviated Maxwell’s whereas the fourth one is the equation that simulates the behavior of the nonlinear medium):
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
where: ![]() and
and ![]() are the corresponding tensor contractions of nonresonance quadratic and cubic nonlinear
are the corresponding tensor contractions of nonresonance quadratic and cubic nonlinear
polarizabilities with unit vectors of polarization of interacting waves;![]() ;
; ![]() is the oscillator
is the oscillator
strength of the oscillation![]() ;
; ![]() is the ratio of effective charge to effective mass for given vibration;
is the ratio of effective charge to effective mass for given vibration; ![]()
is the nonresonance part of dielectric permeability on frequency![]() ;
;![]() ;
;![]() ;
; ![]()
is the tensor of combinational scattering per one elementary cell ;![]() ;
;![]() ;
; ![]() is constant of phonon attenuation;
is constant of phonon attenuation; ![]() -z-components of velocities of waves on
-z-components of velocities of waves on![]() .
.
The asymptotic solution of the system (4)-(7) in form of solitons was found in [12] . Soliton amplitudes ![]() and phases
and phases ![]() were related with
were related with ![]() as follows
as follows
![]() , (8)
, (8)
![]() , (9)
, (9)
where the real amplitudes ![]() and phases
and phases ![]() are considered to be functions of only
are considered to be functions of only ![]() v is the soliton velocity;
v is the soliton velocity; ![]() are the indexes of refraction in linear theory. The soliton solution was found to be of Lorentzian shape:
are the indexes of refraction in linear theory. The soliton solution was found to be of Lorentzian shape:
![]() (10)
(10)
![]() (11)
(11)
where:
![]()
![]()
or
![]()
![]()
![]()
![]() ,
,
![]()
![]()
3. Finite-Difference Equivalent of Basic System of Equations
In this paper, we apply the method of finite differences to show that space-time evolution of impulses is consistent with asymptotic behaviour in form of solitons. For the time derivative the forward difference was applied [11] :
![]() (12)
(12)
For the space derivative the backward difference was applied:
![]() (13)
(13)
The system (4)-(7) can be rewritten as follows
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
where:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The chosen mesh was
![]()
4. Transition Regime of the Stimulated Raman Scattering Solitons
The pulses on laser and Stokes frequencies were chosen to be of Gaussian shape (their amplitudes were proportional to ![]() (the coefficient
(the coefficient ![]() was 0.159155; this was done in order to minimize the transition re-
was 0.159155; this was done in order to minimize the transition re-
gime and to get the area of each pulse close to![]() ). The two-dimensional arrays A for the amplitudes of waves were A [10] [1000] which resulted in 10,000 points for each wave. The conservation of energy (in our case the area under the pulse shape) was monitored by calculating the time integrals for each cross-sectional area in a medium. Since we suggested that the normalized areas of incoming waves (area divided by the amplitude) were equal to
). The two-dimensional arrays A for the amplitudes of waves were A [10] [1000] which resulted in 10,000 points for each wave. The conservation of energy (in our case the area under the pulse shape) was monitored by calculating the time integrals for each cross-sectional area in a medium. Since we suggested that the normalized areas of incoming waves (area divided by the amplitude) were equal to![]() , all those integrals showed the evolution of pulses of Gaussian shape to those of Lorentzian shape with normalized area of
, all those integrals showed the evolution of pulses of Gaussian shape to those of Lorentzian shape with normalized area of ![]() (
(![]() [13] ). The results are shown in Figure 1.
[13] ). The results are shown in Figure 1.
![]()
Figure 1. The space-time evolution of the normalized intensities![]() of laser, Stokes, and polariton pulses.
of laser, Stokes, and polariton pulses.
5. Stability of the Stimulated Raman Scattering Solitons
Let the new amplitudes (amplitudes with disturbances) in unitless form be
![]() (22)
(22)
![]() (23)
(23)
where: ![]() are the unitless amplitudes of waves in presence of disturbance (
are the unitless amplitudes of waves in presence of disturbance (![]() );
);
![]() are the small disturbances;
are the small disturbances; ![]() -is the peak amplitude of the incoming laser pulse;
-is the peak amplitude of the incoming laser pulse;
![]() ;
;![]() ;
;![]() ;
;![]() ; c is the speed of light in vacuum;
; c is the speed of light in vacuum; ![]() is the characteristic time (
is the characteristic time (![]() =
=
1 fs). When we substitute (22) and (23) into the system (4)-(7) we get the system of equations that can be significantly simplified if we consider the evolution of disturbances ![]() in the vicinity of the maximum value of soliton amplitude that is in the case when
in the vicinity of the maximum value of soliton amplitude that is in the case when![]() . In that case the simplified system of equations (the disturbances
. In that case the simplified system of equations (the disturbances ![]() are considered to be small compared to the amplitudes of solitons) becomes that of four linear equations of second order:
are considered to be small compared to the amplitudes of solitons) becomes that of four linear equations of second order:
![]() (24)
(24)
where:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (25)
(25)
where:
![]()
![]()
![]()
![]()
![]() (26)
(26)
where:
![]()
![]()
![]()
![]()
![]() (27)
(27)
where:
![]()
![]()
![]()
![]()
![]()
The system of equations (24)-(27) was solved numerically. The results are presented in Figure 2.
6. Conclusion
The system of eight nonlinear equations describing the SRS with excitation of polar optical phonons was numerically solved. The results of the computer simulation are completely consistent with the asymptotical solutions in form of solitons. It is numerically shown that with SRS on dipole-active phonons the process of propagation of pulses of Gaussian shape on laser and Stokes frequencies results in formation of solitons of Lorentzian shape at all frequencies of interacting waves. Those solitons are stable in wide range of parameters that characterize both the electromagnetic waves and medium.