Alternating Group Explicit Iterative Methods for One-Dimensional Advection-Diffusion Equation

Ning Chen, Haiming Gu^*

College of Mathematics and Physics, Qingdao University of Science and Technology, Qingdao, China.

DOI: 10.4236/ajcm.2015.53025                

Abstract

The finite difference method such as alternating group iterative methods is useful in numerical method for evolutionary equations and this is the standard approach taken in this paper. Alternating group explicit (AGE) iterative methods for one-dimensional convection diffusion equations problems are given. The stability and convergence are analyzed by the linear method. Numerical results of the model problem are taken. Known test problems have been studied to demonstrate the accuracy of the method. Numerical results show that the behavior of the method with emphasis on treatment of boundary conditions is valuable.

Keywords

One-Dimensional Advection-Diffusion Equations, Alternating Group Explicit Iterative Methods, Stability, Convergence, Finite Difference Method

1. Introduction

In this paper, we consider the one-dimensional time-dependent advection-diffusion equations

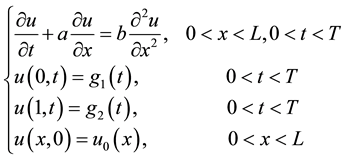(1)

where are known functions while the function is unknown; 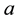and 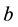are positive constants quantifying the diffusion and advection processes, respectively. Equation (1) describes advection-dif- fusion of quantities such as heat, energy, mass, etc. They find their application in water transfer in soils, heat transfer in draining film, spread of pollutants in rivers and dispersion of tracers in porous media. They are also widely used in studying the spread of solute in a liquid flowing through a tube, long-range transport of pollutants in the atmosphere, flow in porous media and many others (see [1] [2] ). This method has been applied and analyzed for the Timoshenko beam problem, the Reissner-Mindlin plate, the arch problem and the ax symmetric shell problem. As a major contribution for these mixed formulations, this method has overcome the difficulties concerning the usual stability conditions allowing combinations of simple finite element polynomials of almost any order including the attractive equal-order interpolations.

They are also important in many branches of engineering and applied science. These equations are characterized by a non-dissipative (hyperbolic) advective transport component and a dissipative (parabolic) diffusive component. All numerical profiles go well when diffusion is the dominant factor. On the contrary, when advection is dominant transport process, most numerical results exhibit some combination of spurious oscillations and excessive numerical diffusion. These behaviors can be easily explained using a general Fourier analysis. Little progress has been made to overcome such difficulties effectively. Using extremely fine mesh is one alternative but is not prudent to apply it as it is computationally costlier. So a great effort has been made on developing the efficient and stable numerical techniques.

The numerical methods that have been applied to advection-diffusion equation include finite difference methods, Galerkin methods, spectral methods, wavelet based finite elements and several others. The AGE method is an iterative method employing the fractional splitting strategy which is applied alternately at each intermediate step on tridiagonal system of difference schemes. Its rate of convergence is governed by the acceleration parameter. The AGE iterative method is applied to a variety of problems involving parabolic and hyperbolic partial differential equations (see [3] - [6] ). In [7] , Sahimi and Evans reformulated the AGE method to solve the Navier-Stokes equations in the stream function-vorticity form. In this paper we apply the AGE iterative method to the one-dimensional advection diffusion equation. We put forward a new iterative method by numerical differentiation and also extend the original method. The AGE method is shown to be extremely powerful and flexible and affords its users many advantages. Computational results are obtained to demonstrate the applicability of the method on some problems with known solutions.

2. Finite Difference Discretization

Let us divide the domain 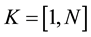into 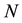equal sized elements of length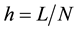. The 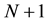nodes have coordinates 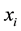with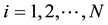. The discrete solution consists of nodal values of the function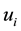, which approximate the exact solution at the nodes. We denote 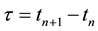be time interval, 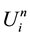be approximation solution, where;,. Let to be a ratio of mesh sizes. In this paper, we special discuss the AGE methods for.

Introduce the following fourth order difference form as

(2)

(3)

Applying the second class Saul’yev asymmetric difference schemes (see [8] ), this leads to the following eight difference form based eight internal grid points as

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

3. AGE Iterative Methods

Now, we can construct AGE iterative forms based on (4)-(11). Let. For the time level, if can be odds, the grid points will be divided into parts. Know that there are eight grid points in each part, and then, we will apply the form (4), (5), …, (11) to find the solution one by one. If can be evens, the grid points will be divided into three sections. At left boundary section, there are four grid points. We can apply the form (8), (9), (10), (11) to find the solution. At middle section, the grid points will be divided into parts. There are eight grid points in each parts, and we will apply the form (4), (5), …, (11) to find the solution one by one. At right boundary section, there are four grid points. We can apply the form (4), (5), (6), (7) to find the solution.

Find, , , , the AGE iterative methods by use (4)-(11) can be written as

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

This may be written in matrix form as

,

where

, ,

where

, ,

and

, , ,

, , , ,

where

, ,

where

,

,.

We know that is nonnegative symmetric matrix and is a skew symmetric matrix.

Let

,

Then the AGE iterative methods in matrix form can be written as

,

,

Similarly, for, we obtain

.

Finally, we will obtain the AGE methods (note to be I) when

(20)

In a similar manner, we can write the AGE algorithm, when is odd.

4. Analysis for the Stability and Convergence

Theorem 4.1. The AGE iterative methods for eight grid points (I) are stable absolutely.

Proof. It is easily to see that the matrix, , are nonnegative.

,

Since, we find that, are nonnegative too.

From (20), we have.

where

,

Note.

Since, are nonnegative matrix, from Kellog’s lemma (see [9] ), we have

we can obtain. The proof of Theorem 4.1 is completed.

Now, we will discuss the convergence for the AGE methods (I).

For (4), (5), …, (11), we can note to be the operator of. Defining, , to be discretization operator corresponding to (4)-(11):

(21)

We have:

(22)

In a similar manner, we can obtain the truncation error as

(23)

(24)

(25)

(26)

(27)

(28)

(29)

Computing by, we can use (4), (6) and (7), (9) alternatively when i = 1, 3. Considering (4) and (27), (6) and (28)

(30)

(31)

Comparing (30) and (26), (31) and (28), we can obtain obviously the truncation error is. Computing by, we can use (4), (6) and (7), (9) alternatively too when i = 2, 4. Considering (6) and (24), (8) and (26)

(32)

(33)

Comparing (32) and (27), (33) and (26), we can obtain obviously the truncation error is too. In the same manner, we can deduce the truncation error for i = 5, 6, 7, 8.

5. Illustrative Examples

To illustrate the proposed AGE and Newton-AGE iterative methods and to demonstrate their convergence computationally, we have solved the following four problems whose exact solutions are known. The right-hand-side functions, initial and boundary conditions may be obtained using the exact solutions. We also have compared the proposed AGE and AGE-4P (see [10] ) iterative methods. We have considered

Its exact solution is,.

Let, , , ,. is approximation solution, and is exact solution.

Define the norm of and,

The rate of the method is

where is the numerical solution with space step size and time step, and is the exact solution. In Table 1, the convergence rates are displayed. In Table 2, the absolute errors are obtained.

We have:

The errors and rate of iterations both for the AGE and AGE-4P methods are tabulated. The errors for the AGE-4P are second order and the new AGE iterative methods (I) are fourth order method. In this paper, we have discussed the AGE and AGE-4P iterative methods for the numerical solution of one-space dimensional advection

Table 1. The comparison of the rate of the convergence by the scheme (I) and AGE-4P.

Table 2. The result of the scheme (I) and AGE-4P.

diffusion equations. The methods are accurate and applicable to problems in both Cartesian and polar coordinates. The proposed AGE and AGE-4P methods show superiority. The development of the AGE group methods implies that parallelism can be easily applied advantageously.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Celia, M.A., Russell, T.F., Herrera, I. and Ewing, R.E. (1990) An Eulerian-Langrangian Localized Adjoint Method for the Advection-Diffusion Equation. Advances in Water Resources, 13, 187-206. http://dx.doi.org/10.1016/0309-1708(90)90041-2
[2]	Dehgan, M. (2004) Weighted Finite Difference Techniques for the One-Dimensional Advection Diffusion Equation. Applied Mathematics and Computation, 147, 307-319. http://dx.doi.org/10.1016/0309-1708(90)90041-2
[3]	Evans, D.J. and Sahimi, M.S. (1988) The Alternating Group Explicit (AGE) Iterative Method for Solving Parabolic Equations. I: Two-Dimensional Problems. International Journal of Computer Mathematics, 24, 311-341. http://dx.doi.org/10.1080/00207168808803651
[4]	Evans, D.J. and Sahimi, M.S. (1989) The Alternating Group Explicit (AGE) Iterative Method to Solve Parabolic and Hyperbolic Partial Differential Equations. Annual Review of Numerical Fluid Mechanics and Heat Transfer, 2, 283-389. http://dx.doi.org/10.1615/AnnualRevHeatTransfer.v2.100
[5]	Evans, D.J. and Sahimi, M.S. (1990) The Solution of Nonlinear Parabolic Partial Differential Equations by the Alternating Group Explicit (AGE) Method. Computer Methods in Applied Mechanics and Engineering, 84, 15-42. http://dx.doi.org/10.1016/0045-7825(90)90087-3
[6]	Evans, D.J. and Sahimi, M.S. (1992) The AGE Solution of the Bi-Harmonic Equation for the Deflection of Uniformly Loaded Square Plate. Report 748, Department of Computer Studies, Loughborough University, Loughborough.
[7]	Sahimi, M.S. and Evans, D.J. (1994) The Numerical Solution of a Coupled System of Elliptic Equations Using the AGE Fractional Scheme. International Journal of Computer Mathematics, 50, 65-87. http://dx.doi.org/10.1080/00207169408804243
[8]	Saul. yev V K. (1998) Integration of Techniques for Fluid Dynamics. Springer-Verlag, Berlin.
[9]	Kellog, G.R.B. (1964) An Alternating Direction Method for Operator Equations. SIAM Journal on Numerical Analysis, 12, 848-854. http://dx.doi.org/10.1137/0112072
[10]	Wang, W.Q. (2002) A Class Alternating Segment Method for Solving Convection-Diffusion Equation. Numerical Mathematics, A Journal of Chinese Universities, 4, 289-297.