Optimal Generalized Biased Estimator in Linear Regression Model ()
1. Introduction
To overcome the multicollinearity problem in the linear regression model, several biased estimators were defined in the place of Ordinary Least Squares Estimator (OLSE) to estimate the regression coefficients, and the properties of these were discussed in the literature. Some of these estimators are based on only sample information such as Ridge Estimator (RE) [1] , Almost Unbiased Ridge Estimator (AURE) [2] , Liu Estimator (LE) [3] and Almost Unbiased Liu Estimator (AULE) [4] . However for each case, the researcher has to obtain their properties and to compare the superiority of one estimator over another estimator when selecting a suitable estimator for a practical situation. Therefore [5] proposed a Generalized Unrestricted Estimator (GURE)  to represent the RE, AURE, LE and AULE, where
to represent the RE, AURE, LE and AULE, where  is the OLSE, and A is a positive definite matrix which depends on the corresponding estimators of RE, AURE, LE and AULE.
is the OLSE, and A is a positive definite matrix which depends on the corresponding estimators of RE, AURE, LE and AULE.
However, the researchers are still trying to find the best estimator by changing the matrix A compared to the already proposed estimators based on sample information. Instead of changing A, in this research we introduce a more efficient new biased estimator based on optimal choice of A.
The rest of the paper is organized as follows. The model specification and estimation is given in Section 2. In Section 3, we propose a biased estimator namely Generalized Optimal Estimator (GOE), and we obtain its stochastic properties. In Section 4 we compare the proposed estimator with some biased estimators in the Scalar Mean Square Error criterion by using a real data set and a Monte Carlo simulation. Finally some conclusion remarks are given in Section 5.
2. Model Specification and Estimation
First we consider the multiple linear regression model
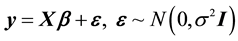 (1)
(1)
where y is an 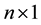 observable random vector, X is an
observable random vector, X is an  known design matrix of rank p,
known design matrix of rank p, 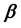 is a
is a 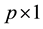 vector of unknown parameters and ε is an
vector of unknown parameters and ε is an 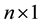 vector of disturbances.
vector of disturbances.
The Ordinary Least Square Estimator of  and
and  are given by
are given by
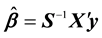 (2)
(2)
and
 (3)
(3)
respectively, where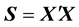 .
.
The Ridge Estimator (RE), Almost Unbiased Ridge Estimator (AURE), Liu Estimator (LE) and Almost Unbiased Liu Estimator (AULE) are some of the biased estimators proposed to solve the multicollinearity problem which are based only on sample information. The estimators are given below:
RE:  where
where  for
for 
LE: ![]() where
where ![]() for
for ![]()
AURE: ![]() where
where ![]() for
for ![]()
AULE: ![]() where
where ![]() for
for ![]()
Since RE, LE, AURE and AULE are based on OLSE, [5] proposed a generalized form to represent these four estimators, the Generalized Unrestricted Estimator (GURE) which is given as
![]() (4)
(4)
where ![]() is a positive definite matrix and
is a positive definite matrix and ![]() stands for w,
stands for w, ![]() ,
, ![]() and
and ![]() .
.
The bias vector, dispersion matrix and MSE matrix of ![]() are given as
are given as
![]() (5)
(5)
![]() (6)
(6)
and
![]() (7)
(7)
respectively.
Instead of changing the matrix ![]() to introduce a new biased estimator, in this research we obtain the optimal choice of
to introduce a new biased estimator, in this research we obtain the optimal choice of ![]() by minimizing the Mean Square Error Matrix (MSEM) of GURE with respect to
by minimizing the Mean Square Error Matrix (MSEM) of GURE with respect to![]() .
.
3. The Proposed Estimator
From (7) the following equation can be obtained by taking trace operator as
![]() (8)
(8)
By minimizing (8) with respect to![]() , the optimum
, the optimum ![]() can be obtained.
can be obtained.
![]() (9)
(9)
where ![]()
Now we can simplify the matrix B as
![]()
Therefore
![]() (10)
(10)
Now we will use the following three results (see [6] , p. 521, 522) to obtain the ![]() and
and![]() .
.
(a) Let M and X be any two matrixes with proper order. Then
![]()
(b) If x is an n-vector, y is an m-vector, and C an ![]() matrix, then
matrix, then
![]()
(c) Let x be a K vector, M a symmetric ![]() matrix, and C a
matrix, and C a ![]() matrix. Then
matrix. Then
![]()
By applying (a) we can obtain
![]() (11)
(11)
Now we consider
![]() (12)
(12)
By using (b) and (c) we can obtain
![]() (13)
(13)
and
![]() (14)
(14)
respectively.
Hence
![]() (15)
(15)
Substituting (11) and (15) to (9), we can derive that
![]() (16)
(16)
Equating (16) to a null matrix, we can obtain the optimal matrix ![]() as
as
![]() (17)
(17)
Note that ![]() exists since
exists since ![]() (see [6] , p. 494).
(see [6] , p. 494).
Now we are ready to propose a biased estimator namely Generalized Optimal Estimator (GOE) as
![]() (18)
(18)
The bias vector, dispersion matrix, mean square error matrix and scalar mean square error of ![]() can be obtained as
can be obtained as
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
and
![]() (22)
(22)
respectively.
Note that since ![]() is symmetric and
is symmetric and ![]() where
where ![]() it can be defined
it can be defined![]() . Then
. Then ![]() and
and![]() . Therefore r is symmetric and idempotent
. Therefore r is symmetric and idempotent
matrix. Now we write the optimal matrix ![]() as
as![]() .
.
Now the bias vector, dispersion matrix, mean square error matrix and scalar mean square error of ![]() can be rewritten as
can be rewritten as
![]() , (23)
, (23)
![]() , (24)
, (24)
![]() (25)
(25)
and
![]() (26)
(26)
respectively.
For practical situations we have to replace the unknown parameters ![]() and
and![]() . For an estimated value for
. For an estimated value for ![]() the OLSE, RE, LE, AURE or AULE can be used. For the estimated value for
the OLSE, RE, LE, AURE or AULE can be used. For the estimated value for ![]() we can use either (2) or replace
we can use either (2) or replace ![]() in (2) by RE, LE, AURE or AULE accordingly. In the next section we will discuss the superiority of estimators when replacing each of these estimated values by using a simulation study, and then we use numerical examples for further illustration.
in (2) by RE, LE, AURE or AULE accordingly. In the next section we will discuss the superiority of estimators when replacing each of these estimated values by using a simulation study, and then we use numerical examples for further illustration.
4. Numerical Illustration
4.1. Monte Carlo Simulation
To study the behavior of our proposed estimator, we perform the Monte Carlo Simulation study by considering different levels of multicollinearity. Following [7] we generate explanatory variables as follows:
![]()
where ![]() is an independent standard normal pseudo random number, and
is an independent standard normal pseudo random number, and ![]() is specified so that the theoretical correlation between any two explanatory variables is given by
is specified so that the theoretical correlation between any two explanatory variables is given by![]() . A dependent variable is generated by using the equation.
. A dependent variable is generated by using the equation.
![]()
where ![]() is a normal pseudo random number with mean zero and variance
is a normal pseudo random number with mean zero and variance![]() . [8] have noted that if the MSE is a function of
. [8] have noted that if the MSE is a function of ![]() and
and![]() , and if the explanatory variables are fixed, then subject to the constraint
, and if the explanatory variables are fixed, then subject to the constraint![]() , the MSE is minimized when
, the MSE is minimized when ![]() is the normalized eigenvector corresponding to the largest eigenvalue of the
is the normalized eigenvector corresponding to the largest eigenvalue of the ![]() matrix. In this study we choose the normalized eigenvector corresponding to the largest eigenvalue of
matrix. In this study we choose the normalized eigenvector corresponding to the largest eigenvalue of ![]() as the coefficient vector
as the coefficient vector![]() ,
, ![]() ,
, ![]() and
and![]() . Four different sets of correlations are considered by selecting the values as
. Four different sets of correlations are considered by selecting the values as![]() , 0.9, 0.99 and 0.999.
, 0.9, 0.99 and 0.999.
Table 1 can be obtained by using estimated SMSE values obtained by using equations (7) and (21) for different shrinkage parameter d or k values selected from the interval (0, 1). The SMSE of GOE-OLSE, GOE-RE, GOE-LE, GOE-AURE and GOE-AULE are obtained by substituting OLSE, RE, LE, AURE and AULE in equation (21) respectively instead of ![]() and
and![]() .
.
According to Table 1, we can say that the GOE-OLSE has the smallest scalar mean square error values with compared to RE, LE, AURE, AULE, GOE-RE, GOE-LE, GOE-AURE and GOE-AULE when γ = 0.8, 0.9, 0.99 and 0.999.
4.2. Numerical Example
To further illustrate the behavior of our proposed estimator we consider two data sets. First we consider the data set on Portland cement originally due to [9] . This data set has since then been widely used by many researchers such as [10] - [13] . This data set came from an experimental investigation of the heat evolved during the setting and hardening of Portland cements of varied composition and the dependence of this heat on the percentages of four compounds in the clinkers from which the cement was produced. The four compounds considered by [9] are tricalium aluminate: 3CaO∙Al2O3, tricalcium silicate: 3CaO∙SiO2, tetracalcium aluminaferrite: 4CaO∙Al2O3∙Fe2O3, and beta-dicalcium silicate: 2CaO∙SiO2, which we will denote by![]() ,
, ![]() ,
, ![]() and
and![]() , respectively. The dependent variable y is the heat evolved in calories per gram of cement after 180 days of curing.
, respectively. The dependent variable y is the heat evolved in calories per gram of cement after 180 days of curing.
![]()
Table 1. Estimated SMSE values of the RE, LE, AURE, AULE, GOE-OLSE, GOE-RE, GOE-LE, GOE-AURE and GOE- AULE when γ = 0.8, 0.9, 0.99 and 0.999.
We assemble our data set in the matrix form as follows:
![]() .
.
For this particular data set, we obtain the following results:
a) The eigen values of![]() : 105, 810, 5965, 44663
: 105, 810, 5965, 44663
b) The condition number = 20.58464
c) The OLSE of ![]() is
is![]() :
: ![]()
d) The OLSE of![]() :
:![]() .
.
Table 2 can be obtained by using estimated SMSE values obtained by using Equations (7) and (21) for different shrinkage parameter d or k values selected from the interval (0, 1). The SMSE of GOE-OLSE, GOE-RE, GOE-LE, GOE-AURE and GOE-AULE are obtained by substituting OLSE, RE, LE, AURE and AULE in Equation (21) respectively instead of ![]() and
and![]() .
.
From Table 2 we can notice that the GOE-OLSE, GOE-RE, GOE-LE, GOE-AURE and GOE-AULE have the smallest scalar mean square error value with compared to RE, LE, AURE, AULE. Therefore we can suggest the GOE to estimate the regression coefficients. When k is large, GOE-OLSE has smallest SMSE than GOE-RE. When d is small, GOE-OLSE has smallest SMSE than GOE-LE.
Now we consider the second data set on Total National Research and Development Expenditures as a Percent of Gross National product originally due to [14] , and later considered by [15] - [17] .
![]()
Table 2. Estimated SMSE values of RE, LE, AURE, AULE, GOE-OLSE, GOE-RE, GOE-LE, GOE-AURE and GOE- AULE the data set on Portland Cement.
The data set is given below:
![]()
The four column of the 10 × 4 matrix ![]() comprise the data on
comprise the data on![]() ,
, ![]() ,
, ![]() and
and ![]() respectively, and y is the predictor variable.
respectively, and y is the predictor variable.
For this particular data set, we obtain the following results:
a) The eigen values of![]() : 302.9626, 0.7283, 0.7283 and 0.00345
: 302.9626, 0.7283, 0.7283 and 0.00345
b) The condition number = 93.68
c) The OLSE of ![]() is
is ![]()
d) The OLSE of![]() :
:![]() .
.
Table 3 can also be obtained by using estimated SMSE values obtained by using Equations (7) and (21) for different shrinkage parameter d or k values selected from the interval (0, 1). The SMSE of GOE-OLSE, GOE-RE, GOE-LE, GOE-AURE and GOE-AULE are obtained by substituting OLSE, RE, LE, AURE and AULE in Equation (21) respectively instead of ![]() and
and![]() .
.
From Table 3, we can say that our proposed estimator is superior to RE, LE, AURE and AULE, GOE-RE, GOE-LE, GOE-AURE and GOE-AULE.
5. Conclusions
In this paper we proposed a new biased estimator namely Generalized Optimal Estimator (GOE) in a multiple linear regression when there exists multicollinearity problem in the independent variables. The proposed estimator is superior to biased estimators which are based on sample information and takes the form![]() . Based on Tables 1-3, it can be concluded that the proposed estimator has smallest scalar mean square error values com- pared with RE, LE, AURE and AULE. We can also suggest that GOE-OLSE is the best estimator with compared to GOE-RE, GOE-LE, GOE-AURE and GOE-AULE.
. Based on Tables 1-3, it can be concluded that the proposed estimator has smallest scalar mean square error values com- pared with RE, LE, AURE and AULE. We can also suggest that GOE-OLSE is the best estimator with compared to GOE-RE, GOE-LE, GOE-AURE and GOE-AULE.
![]()
Table 3. Estimated SMSE values of RE, LE, AURE, AULE, GOE-OLSE, GOE-RE, GOE-LE, GOE-AURE and GOE-AULE the data set on total national research and development expenditures.
Acknowledgements
We thank the Postgraduate Institute of Science, University of Peradeniya, Sri Lanka for providing all facilities to do this research.