On the Signed Domination Number of the Cartesian Product of Two Directed Cycles ()
1. Introduction
Throughout this paper, a digraph 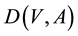 always means a finite directed graph without loops and multiple arcs, where
always means a finite directed graph without loops and multiple arcs, where  is the vertex set and
is the vertex set and 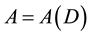 is the arc set. If uv is an arc of D, then say that v is an out-neighbor of u and u is an in-neighbor of v. For a vertex
is the arc set. If uv is an arc of D, then say that v is an out-neighbor of u and u is an in-neighbor of v. For a vertex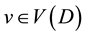 , let
, let 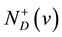 and
and  denote the set of out-neighbors and in-neighbors of v, respectively. We write
denote the set of out-neighbors and in-neighbors of v, respectively. We write 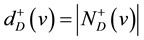 and
and 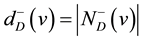 for the out-degree and in-degree of v in D, respectively (shortly
for the out-degree and in-degree of v in D, respectively (shortly ,
,![]() ). A digraph D is r-regular if
). A digraph D is r-regular if ![]() for any vertex
for any vertex![]() . Let
. Let ![]() and
and![]() . The maximum out-degree and in-degree of D are denoted by
. The maximum out-degree and in-degree of D are denoted by ![]() and
and![]() , respectively (shortly D+, D−). The minimum out-degree and in-degree of D are denoted by
, respectively (shortly D+, D−). The minimum out-degree and in-degree of D are denoted by ![]() and
and![]() , respectively (shortly
, respectively (shortly![]() ,
,![]() ). A signed dominating function of D is defined in [1] as function
). A signed dominating function of D is defined in [1] as function ![]() such that
such that ![]() for every vertex
for every vertex![]() . The signed domination number of a directed graph D is
. The signed domination number of a directed graph D is ![]() . Also, a signed k-dominating function (SKDF) of D is a function
. Also, a signed k-dominating function (SKDF) of D is a function
![]() such that
such that ![]() for every vertex
for every vertex![]() . The k-signed domination number of a di-
. The k-signed domination number of a di-
graph D is![]() . Consult [2] for the notation and terminology which are not defined here.
. Consult [2] for the notation and terminology which are not defined here.
The Cartesian product ![]() of two digraphs D1 and D2 is the digraph with vertex set
of two digraphs D1 and D2 is the digraph with vertex set ![]()
![]() and
and ![]() if and only if either
if and only if either ![]() and
and ![]() or
or ![]() and
and![]() .
.
In the past few years, several types of domination problems in graphs had been studied [3] -[7] , most of those belonging to the vertex domination. In 1995, Dunbar et al. [3] , had introduced the concept of signed domination number of an undirected graph. Haas and Wexler in [1] , established a sharp lower bound on the signed domination number of a general graph with a given minimum and maximum degree and also of some simple grid graph. Zelinka [8] initiated the study of the signed domination numbers of digraphs. He studied the signed domination number of digraphs for which the in-degrees did not exceed 1, as well as for acyclic tournaments and the circulant tournaments. Karami et al. [9] established lower and upper bounds for the signed domination number of digraphs. Atapour et al. [10] presented some sharp lower bounds on the signed k-domination number of digraphs. Shaheen and Salim in [11] , were studied the signed domination number of two directed cycles Cm ´ Cn when m = 3, 4, 5, 6, 7 and arbitrary n. In this paper, we study the Cartesian product of two directed cycles Cm and Cn for mn ≥ 8n. We mainly determine the exact values of![]() ,
, ![]() ,
, ![]() and for some values of m and n. Some previous results:
and for some values of m and n. Some previous results:
Theorem 1.1 (Zelinka [8] ). Let D be a directed cycle or path with n vertices. Then![]() .
.
Lemma 1.2 (Zelinka [8] ). Let D be a directed graph with n vertices. Then![]() .
.
Corollary 1.3 (Karami et al. [9] ). Let D be a directed of order n in which ![]() for each
for each
![]() , where k is a nonnegative integer. Then
, where k is a nonnegative integer. Then![]() .
.
In [11] , the following results are proved.
Theorem 1.4 [11] :
![]() , otherwise
, otherwise![]() .
.![]() .
.
![]() , ,
, ,
![]() ,.
,.
![]() , otherwise
, otherwise![]() .
.![]() .
.
2. Main Results
In this section we calculate the signed domination number of the Cartesian product of two directed cycles Cm and Cn for m = 8, 9, 10 and ![]() and arbitrary n.
and arbitrary n.
The vertices of a directed cycle Cn are always denoted by theintegers ![]() considered modulo n. The ith row of
considered modulo n. The ith row of ![]() is
is ![]() and the jth column
and the jth column![]() . For any vertex
. For any vertex![]() , always we have the indices i and j are reduced modulo m and n, respectively.
, always we have the indices i and j are reduced modulo m and n, respectively.
Let us introduce a definition. Suppose that f is a signed dominating function for Cm ´ Cn, and assume that![]() . We say that the hth column of
. We say that the hth column of ![]() is a t-shift of the jth column if
is a t-shift of the jth column if ![]() for each vertex
for each vertex![]() , where the indices i, t, i + t are reduced modulo m and j, h are reduced modulo n.
, where the indices i, t, i + t are reduced modulo m and j, h are reduced modulo n.
Remark 2.1: Let f is a ![]() -function. Then
-function. Then ![]() for each
for each ![]() and each
and each![]() .
.
Since Cm × Cn is 2-regular, it follows from ![]() that
that ![]() because
because ![]() ,
, ![]() because
because ![]() and
and ![]() because
because
![]() . On the other hand, if
. On the other hand, if![]() ,
, ![]() and
and
![]() , then we must have
, then we must have ![]() since f is a minimum signed dominating function.
since f is a minimum signed dominating function.
Remark 2.2. Since the case ![]() is not possible, we get sj ≥ 0. Furthermore, sj is odd if m is odd and even when m is even.
is not possible, we get sj ≥ 0. Furthermore, sj is odd if m is odd and even when m is even.
Let f be a signed dominating function for Cm ´ Cn, then we denote ![]() of the weight of a
of the weight of a
column Kj and put![]() . The sequence
. The sequence ![]() is called a signed dominating sequence corresponding to f. We define
is called a signed dominating sequence corresponding to f. We define
![]()
Then we have
![]()
![]()
For the remainder of this section, let f be a signed domination function of Cm × Cn with signed dominating sequence![]() . We need the following Lemma:
. We need the following Lemma:
Lemma 2.3. If ![]() then
then![]() . Furthermore,
. Furthermore, ![]() and
and![]() .
.
Proof. Let![]() , then there are
, then there are ![]() of vertices in Kj which get value −1. By Remark 2.1,
of vertices in Kj which get value −1. By Remark 2.1, ![]() include at least
include at least ![]() of vertices which get the value 1 and at most
of vertices which get the value 1 and at most ![]() of vertices which has value −1. Hence,
of vertices which has value −1. Hence,![]() . Furthermore,
. Furthermore,![]() . By the same argument, we get
. By the same argument, we get ![]() and
and![]() . □
. □
Theorem 2.4.
![]()
Proof. We define a signed dominating function f as follows:
![]() for and,
for and,
![]() for
for ![]() and
and![]() , and
, and
![]() otherwise. Also we define
otherwise. Also we define ![]() for
for![]() .
.
By the definition of f, we have sj = 2 for j is odd and sj = 4 for j is even. Notice, f is a SDF for C8 × Cn when![]() . Therefore, there is a problem with the vertices of K1 when
. Therefore, there is a problem with the vertices of K1 when![]() .
.
Now, let us define the following functions:
![]() ,
,
![]() ,
,
We note:
f1 is a SDF of C8 × Cn when![]() .
.
f2 is a SDF of C8 × Cn when![]() .
.
f3 is a SDF of C8 × Cn when![]() .
.
f4 is a SDF of C8 × Cn when![]() .
.
Hence,
![]() (1)
(1)
For example, f1 is a SDF of C8 × C12, where![]() , see Figure 1.
, see Figure 1.
{Here, we must note that, for simplicity of drawing the Cartesian products of two directed cycles Cm × Cn, we do not draw the arcs from vertices in last column to vertices in first column and the arcs from vertices in last row to vertices in first row. Also for each figure of Cm × Cn, we replace it by a corresponding matrix by signs − and + which descriptions −1 and +1 on figure of![]() , respectively}.
, respectively}.
By Remark 2.2, for any minimum signed dominating function f of C8 × Cn with signed dominating sequence![]() , we have sj = 0, 2, 4, 6 or 8 for
, we have sj = 0, 2, 4, 6 or 8 for![]() . By Lemma 2.3, if sj = 0 then
. By Lemma 2.3, if sj = 0 then![]() , and if sj = 2 then
, and if sj = 2 then![]() . This implies that
. This implies that
![]() (2)
(2)
![]() (3)
(3)
Hence, by (1), (2) and (3) we get
![]() .
.
![]() .
.
Assume that![]() .
.
Let f' ba a signed dominating function with signed dominating sequence![]() .
.
If m, n ≤ 7, then by Theorem 1.4 is the required (because![]() ). Let m, n ≥ 8. We prove the following claim:
). Let m, n ≥ 8. We prove the following claim:
Claim 2.1. For k ≥ 2, we have ![]() if k is even and
if k is even and ![]() when k is odd.
when k is odd.
![]() (a) (b)
(a) (b)
Figure 1. (a) A signed dominating function of C8 × C12; (b) A corresponding matrix of a signed dominating function of C8 × C12.
Proof of Claim 2.1. We have the subsequence ![]() is including at least two terms. Then, immediately from Remark 2.2 and Lemma 2.3, gets the required. The proof of Claim 2.1 is complete. □
is including at least two terms. Then, immediately from Remark 2.2 and Lemma 2.3, gets the required. The proof of Claim 2.1 is complete. □
Now, if ![]() for some j, then
for some j, then![]() . Without loss of generality, we can assume that
. Without loss of generality, we can assume that![]() . Then Claim 2.1, imply that
. Then Claim 2.1, imply that
![]() (4)
(4)
Assume that ![]() for all
for all![]() . We have three cases:
. We have three cases:
Case 1. If ![]() for some j. Let
for some j. Let![]() . Then from Claim 2.1, we get
. Then from Claim 2.1, we get
![]() (5)
(5)
![]() (6)
(6)
Case 2. Let![]() . If
. If ![]() include at least two terms which are equals 6, then
include at least two terms which are equals 6, then
![]() (7)
(7)
For![]() , then 8n is even. By Lemma 1.2,
, then 8n is even. By Lemma 1.2, ![]() must be even number. Hence, from (7) is
must be even number. Hence, from (7) is
![]() (8)
(8)
Assume that ![]() for all
for all ![]() except once which equals 6. Thus,
except once which equals 6. Thus,
![]() (9)
(9)
![]() (10)
(10)
For the case 3, we need the following claim:
Claim 2.2. Let f' be a minimum signed dominating function of C8 × Cn with signed dominating sequence![]() .Then for
.Then for![]() , and up to isomorphism, there is only one possible configuration for f", it is shown in Figure 2. The prove is immediately by drawing. □
, and up to isomorphism, there is only one possible configuration for f", it is shown in Figure 2. The prove is immediately by drawing. □
Case 3. Let ![]() for all
for all![]() . We define
. We define
![]()
Then we have
![]()
![]()
Since the case ![]() is not possible, we have
is not possible, we have![]() .
.
If![]() . Then
. Then![]() . Thus
. Thus
![]() (11)
(11)
![]() (12)
(12)
If![]() . Then
. Then![]() . Hence
. Hence
![]() (13)
(13)
![]() (14)
(14)
Let ![]() and
and![]() .
.
Then we have one possible is as the form![]() . This implies that
. This implies that ![]() for
for ![]() and
and ![]() for
for![]() . By Claim 2.2, we have f' is as the function f, which defined in forefront of Theorem 2.4. However, f is not be a signed dominating function for C8 × Cn when
. By Claim 2.2, we have f' is as the function f, which defined in forefront of Theorem 2.4. However, f is not be a signed dominating function for C8 × Cn when![]() . Thus
. Thus
![]()
![]()
By Lemma 1.2, and above arguments, we conclude that
![]() (15)
(15)
![]() (16)
(16)
Hence, from (1), (15) and (16), deduce that
![]()
![]()
![]()
![]()
Finally, we result that:
![]()
![]()
![]()
![]()
![]()
![]() □
□
Theorem 2.5.
![]()
Proof. We define a signed dominating function f as follows: ![]() for
for ![]() and
and![]() , and
, and ![]() otherwise. Also, let us define the following function:
otherwise. Also, let us define the following function:
![]()
By define f, we have sj = 3 for![]() . Notice, f is a SDF for C9 × Cn for
. Notice, f is a SDF for C9 × Cn for![]() . And f1 is a SDF of C9 × Cn for
. And f1 is a SDF of C9 × Cn for![]() . For an illustration
. For an illustration![]() , see Figure 3. Hence,
, see Figure 3. Hence,
![]() (17)
(17)
![]() (18)
(18)
From Corollary 1.3 is![]() . Then by (17),
. Then by (17), ![]() for
for![]() .
.
For![]() .
.
If![]() , then by Theorems 1.4 and 2.4, gets the required. Assume that n ≥ 9.
, then by Theorems 1.4 and 2.4, gets the required. Assume that n ≥ 9.
By Remark 2.2, we have sj = 1, 3, 5, 7 or 9. By Lemma 2.3, if sj = 1 then![]() , sj = 3 then
, sj = 3 then ![]() and sj = 5 then
and sj = 5 then ![]() (because if
(because if![]() , then we need sj ≥ 7). By Lemma 2.3, the
, then we need sj ≥ 7). By Lemma 2.3, the
cases ![]() are not possible. Hence,
are not possible. Hence, ![]() , for k ≥ 2. This implies that,
, for k ≥ 2. This implies that,
![]() (19)
(19)
We define
![]()
Then we have
![]()
Figure 3. A corresponding matrix of a signed dominating function of C9 × C6.
![]()
![]()
If we have one case from the cases X9 ≥ 1, X7 ≥ 2, X5 + X7 ≥ 2 or X5 ≥ 3. Then by (19) is![]() .
.
Assume the contrary, i.e., (X9 = 0, X7 < 2, X5 + X7 < 2 and X5 < 3).
Hence,![]() . We consider the cases X7 < 2 and X5 < 3, which are including the remained cases, i.e., X7 = 1 and X5 = 2. First, we give the following Claim:
. We consider the cases X7 < 2 and X5 < 3, which are including the remained cases, i.e., X7 = 1 and X5 = 2. First, we give the following Claim:
Claim 2.3. There is only one possible for ![]() is
is
![]() and
and
![]() , otherwise for
, otherwise for![]() .
.
The proof comes immediately by the drawing. □
Case 1. X7 = 1 and X5 = X9 = 0. Without loss of generality, we can assume sn = 7. Then we have the form![]() . By Claim 2.3, for
. By Claim 2.3, for![]() , each column
, each column ![]() is 1-shift of Kj,
is 1-shift of Kj, ![]() is 2-shift of Kj and
is 2-shift of Kj and ![]() is 3-shift = (0-shift) of Kj. Without loss of generality, we can assume
is 3-shift = (0-shift) of Kj. Without loss of generality, we can assume ![]() and
and ![]() otherwise. We consider two subcases:
otherwise. We consider two subcases:
Subcase 1.1. For![]() . Then
. Then ![]() is (n − 2)-shift = (2-shift) of K1. This implies that
is (n − 2)-shift = (2-shift) of K1. This implies that ![]() . Hence, we need
. Hence, we need ![]() for all
for all![]() . This is a contradiction with
. This is a contradiction with![]() . Thus,
. Thus,![]() .
.
Subcase 1.2. For![]() . Then
. Then ![]() is (n − 2)-shift = (0-shift) of K1. This implies that
is (n − 2)-shift = (0-shift) of K1. This implies that ![]() . So, we need
. So, we need ![]() for all
for all![]() . Again, we get a contradiction with
. Again, we get a contradiction with![]() . Thus,
. Thus,![]() .
.
Case 2. X5 = 2 and![]() . Here we have
. Here we have ![]() and sj = 3 otherwise. By the same argument similar to the Case 1, we have Kj is (j − 1)-shift of K1. Thus, if
and sj = 3 otherwise. By the same argument similar to the Case 1, we have Kj is (j − 1)-shift of K1. Thus, if![]() , then
, then ![]() and for
and for ![]() is
is![]() . Also, for position the vertices of K1, we always have
. Also, for position the vertices of K1, we always have ![]() . We consider four Subcases:
. We consider four Subcases:
Subcase 2.1. d = 1, without loss of generality, we can assume![]() .
.
For![]() ,
,![]() . Then
. Then ![]() . The three remaining vertices from each
. The three remaining vertices from each ![]() and Kn, most including two values −1, and this is impossible. The same arguments is for
and Kn, most including two values −1, and this is impossible. The same arguments is for![]() .
.
Subcase 2.2. d = 2, let![]() . Then we have the form
. Then we have the form![]() .
.
If n º 1(mod 3), then![]() . This implies that
. This implies that ![]() is 0-shift of K1. Therefore,
is 0-shift of K1. Therefore, ![]() . Hence, the three columns
. Hence, the three columns ![]() must be including seven values of −1, two in
must be including seven values of −1, two in![]() , three in
, three in ![]() and two in Kn and this impossible. The same argument is for n º 2(mod 3).
and two in Kn and this impossible. The same argument is for n º 2(mod 3).
Subcase 2.3. d = 3, let![]() . We have the form
. We have the form![]() . Then for
. Then for![]() ,
, ![]() is 2-shift of K1. Therefore
is 2-shift of K1. Therefore![]() . Also,
. Also, ![]() . Therefore, two vertices of
. Therefore, two vertices of ![]() must has value −1. By symmetry, let
must has value −1. By symmetry, let![]() . Then by Claim 2.3, there is one case for
. Then by Claim 2.3, there is one case for![]() . Hence,
. Hence, ![]() . Therefore, we need two vertices from Kn with value −1. This is a contradiction, (because the vertices of the first column must be a signed dominates by the vertices of the last column). The same argument is for
. Therefore, we need two vertices from Kn with value −1. This is a contradiction, (because the vertices of the first column must be a signed dominates by the vertices of the last column). The same argument is for![]() .
.
Subcase 2.4. d ≥ 4, let ![]() (by symmetry is
(by symmetry is![]() ).
).
We have the form![]() . By Claim 2.3, if
. By Claim 2.3, if ![]() then for each two vertices
then for each two vertices ![]() we must have
we must have ![]() and so for
and so for![]() . Since
. Since ![]() and
and![]() , then
, then ![]() including two vertices with value −1 by 1-shift of two vertices in
including two vertices with value −1 by 1-shift of two vertices in![]() . Also,
. Also, ![]() including two vertices with value −1 by 1-shift of vertices in
including two vertices with value −1 by 1-shift of vertices in ![]() and the third ver- tex must be distance 3 from any one has value −1 (Since
and the third ver- tex must be distance 3 from any one has value −1 (Since![]() , Claim 2.3). Thus, the order of the values −1 or 1 of the vertices
, Claim 2.3). Thus, the order of the values −1 or 1 of the vertices ![]() does not change. Hence the vertices of
does not change. Hence the vertices of ![]() has the same order of
has the same order of ![]() when we have the signed dominating sequence
when we have the signed dominating sequence ![]() and this impossible is signed dominating sequence of C9 × Cn for
and this impossible is signed dominating sequence of C9 × Cn for![]() . In Subcases 2.1, 2.2, 2.3 and 2.4 there are many details, we will be omitted it.
. In Subcases 2.1, 2.2, 2.3 and 2.4 there are many details, we will be omitted it.
Finally, we deduce that does not exist a signed dominating function f of C9 × Cn for ![]() with
with![]() . Hence,
. Hence,
![]() (20)
(20)
From (18) and (20) is![]() . □
. □
Theorem 2.6.![]() .
.
Proof. We define a signed dominating function f as follows:
![]() for
for ![]() and i º j(mod 10), and
and i º j(mod 10), and ![]() otherwise. Also, we define
otherwise. Also, we define
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
and ![]() otherwise for
otherwise for![]() .
.
By define f and ![]() we have sj = 4 for all
we have sj = 4 for all![]() . Notice that: f is a SDF for C10 × Cn when
. Notice that: f is a SDF for C10 × Cn when![]() .
.
![]()
is a SDF for C10 × Cn when![]() .
.
![]()
is a SDF for C10 × Cn when![]() .
.
![]()
is a SDF for C10 × Cn when![]() .
.
![]()
is a SDF for C10 × Cn when![]() .
.
![]()
is a SDF for C10 × Cn when![]() .
.
![]()
is a SDF for C10 × Cn when![]() .
.
![]()
is a SDF for C10 × Cn when![]() .
.
![]()
is a SDF for C10 × Cn when![]() .
.
For an illustration ![]() see Figure 4, (here for
see Figure 4, (here for![]() , we are changing the functions of the columns:
, we are changing the functions of the columns:![]() ). In all the cases we have
). In all the cases we have![]() .
.
By Remark 2.2, we have sj = 0, 2, 4, 6, 8 or 10. Also by Lemma 2.3, if sj = 0, then ![]() and when sj = 2, is
and when sj = 2, is ![]() and sj = 4 is
and sj = 4 is ![]() (because if
(because if ![]() or
or![]() , then sj ≥ 6). This implies that
, then sj ≥ 6). This implies that
![]()
So, we get![]() . □
. □
Corollary 2.7. For![]() , we have
, we have
![]()
![]()
Proof. By Corollary 1.3 we have
![]() (21)
(21)
Let us a signed dominating function f as follows: ![]() for
for![]() ,
, ![]() ,
, ![]() for
for![]() ,
, ![]() , and
, and ![]() for
for![]() ,
,![]() .
.
By define f, we have sj = m/3 for![]() . Notice, f is a SDF for Cm × Cn for
. Notice, f is a SDF for Cm × Cn for![]() . Hence,
. Hence,![]() . Then from (21), is
. Then from (21), is ![]() for
for![]() .
.
For n º 1, 2(mod 3).
Let ![]() for
for![]() . Notice,
. Notice, ![]() is a SDF for Cm × Cn for
is a SDF for Cm × Cn for![]() .
.
Thus,![]() . Hence, by (21) is
. Hence, by (21) is ![]() if
if![]() . □
. □
![]()
Figure 4. A corresponding matrix of a signed dominating function of C10 × C11.
3. Conclusions
This paper determined that exact value of the signed domination number of Cm × Cn for m = 8, 9, 10 and arbitrary n. By using same technique methods, our hope eventually lead to determination ![]() for general m and n.
for general m and n.
Based on the above (Lemma 2.3 and Theorems 1.4, 2.4, 2.5 and 2.6), also by the technique which used in this paper, we again rewritten the following conjecture (This conjecture was mention in [11] ):
Conjecture 3.1.
![]()