Phase-Field Modeling for the Three-Dimensional Space-Filling Structure of Metal Foam Materials ()
1. Introduction
Porous materials are some of the most prospective advanced materials and have begun to be widely used in various engineering fields, utilizing their advantageous properties such as the light weight, heat adiabaticity, and sound and vibration insulation properties. In particular, metal foam materials are expected to make a great contribution to reducing the weight of parts and conserve energy to run machines [1] [2] . Therefore, the development of metal foam materials has been actively pursued. The properties of this type of material are determined not only by the selection of the base material but also by the structure of the internal pores; microscopic characteristics, such as the morphology of each pore and arrangement of multiple pores, affect the macroscopic material properties. Therefore, the control of the microscopic structure is one of the key factors used in designing the material.
Porous materials are divided into two types: open and closed cells. The latter, which is focused in this study, consists of many small cells separated by a wall made of the base material, and the cells are usually polyhedral with rounded corners. These structures are approximated by foam structures, typical examples of which are found in soap and beer, even though the wall of the foam is usually liquid. Neglecting the fluidity of the wall, the geometrical characteristics have many similarities, and hence, the analysis of such foam structures is expected to make a great contribution to the design of porous materials.
The analysis of foam structures dates back to the historical works of Plateau in the 1870s, and his insight on the cell boundary remains used with his name, the Plateau boundary. Lord Kelvin also leaves his name in the Kelvin cell, which is known as a preferable candidate of the foam model and was long considered the best solution for the so-called Kelvin problem, “which shape of cells have the least surface area when the space is divided into cells having the same volume?,” before Weaire and Phelan found a better solution in 1994 [3] . In any case, these divisions are geometrically ideal cell divisions under equal volume restriction, and realistic foam is more complicated. Even allowing that the structure can be simplified and approximated by these models as the equilibrium state, the dynamic processes of formation and destruction are more complicated. The mechanism of these processes has also long been investigated; however, it remains a controversial topic, and no clear theoretical solution has been found [4] . Therefore, computer simulations are expected to provide a promising tool to determine the stable structure and clarify the formation mechanism. The author proposed the application of the phase field model to this problem and presented a two-dimensional simulation showing its availability [5] based on the volume constraint model, which was previously proposed in [6] [7] . In this study, the model is extended to a three-dimensional description, and the reproducibility of the stable structures is discussed.
2. Fundamental Equations
In our previous study [5] , the fundamental equations for the two-dimensional simulation were presented. The phase field model is based on the multi-phase field model developed by Steinbach et al. [8] [9] and modified to constrain the grain growth by controlling the driving force. Similar modification was also proposed by Nestler et al. [10] , in which the volume fraction of each domain is assumed to be preserved from the initial state. In our model, in contrast, the adjacent domains interact with each other and adjust their volume to equalize the cell size. In this study, our previous model is revised to the three-dimensional form by reformulating the corresponding term to control the cell size. In addition, all the equations and parameters are standardized, and the final phase field equation used in this study is as follows:
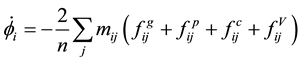 (1)
(1)
where,
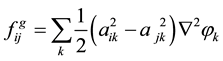 (2)
(2)
 (3)
(3)
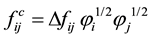 (4)
(4)
and
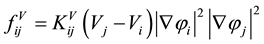 (5)
(5)
Here, φi (i = 1 − N) represents the multi-phase field variable, where N is the number of phases considered; mij, aij, wij, and Δfij are the parameters depending on the combination of i and j; and n is the number of phases for which φi is non-zero. The last term 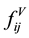 is the revised term corresponding to the expansion from the two-dimen- sional to the three-dimensional model, where Vi is the volume of the i-th cell and
is the revised term corresponding to the expansion from the two-dimen- sional to the three-dimensional model, where Vi is the volume of the i-th cell and 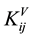 is an adjusting coefficient. The values for the simulation are listed in Table 1. Note that these values are standardized to be dimensionless values.
is an adjusting coefficient. The values for the simulation are listed in Table 1. Note that these values are standardized to be dimensionless values.
3. Model and Conditions
The phase field Equation (1) is numerically solved using the finite difference method (FDM). A cubic domain is divided into 100 × 100 × 100 isotropic lattices, and periodic boundary conditions are imposed in all directions. The differential terms in the right-hand side are discretized on the FDM grids by central difference scheme, and the time derivative is explicitly solved. Independent phase field variables φi (i = 1 − N) are assigned to every cell such that φi = 1 represents the inside region of the i-th cell. This value shifts to 0 in a thin domain surrounding the cell; two different phase-field variables have non-zero values in the cell wall region, and three or more variables have a certain value at edge domains. Note that in any case, the summation of the phase field variables is always maintained to be 1 , and the original bulk metal phase is represented by i = 0. The cell struc-
, and the original bulk metal phase is represented by i = 0. The cell struc-
ture is formed by growing the cells from the nuclei, which is disposed as the initial condition. In this study, the nuclei are set on the regular body-centered cubic (bcc) or face-centered cubic (fcc) lattice points in Section 4.1 and Section 4.2, and random assignment is performed in Section 4.3. The computational parameters Δx and Δt are also listed in Table 1, where Δx is the lattice interval for the finite-difference calculation and Δt is the time increase for numerical integration.
4. Results and Discussion
4.1. Perfect Nuclei Arrangement―Standard Results
Figure 1 presents the simulation results obtained by the regularly arranged nuclei, which are set on (a) bcc and (b) fcc lattice points. The total number of nuclei is 16 for bcc and 32 for fcc, both of which correspond to 2 × 2 × 2 unit cells. In these figures, grids for FDM are plotted with the color identifying the major phase field variable, and only those in the cell boundary region are depicted. One of the typical cells is also selected and shown alongside the figure. In the figures of the selected cells, the color indicates the value of Σφi2; the cell face and edge are represented mostly by green and blue, respectively.
![]() (a) (b)
(a) (b)
Figure 1. Regular space-filling structure and individual cell shape obtained by nuclei set on complete points of bcc or fcc lattices. (a) Bcc-type arrangement; (b) Fcc-type arrangement.
![]()
Table 1. Parameters used for simulations in this study.
Because all the nuclei are set on a completely regular interval, the final cell distribution is also completely regular; these structures actually correspond to the Voronoi tessellations of bcc or fcc lattices. For the bcc arrangement, as shown in Figure 1(a), each cell forms a truncated octahedron, which consists of 6 square faces and 8 hexagons, as shown in Figure 1(a)(ii). This structure is considered stable and is known as a Kelvin cell. For the fcc arrangement, rhombic dodecahedra, each of which consists of 12 rhombic faces, form the space- filling structure, as shown in Figure 1(b). This structure also exhibits high regularity but has a slight disadvantage compared with the Kelvin cell as all the vertices are not equivalent. There are two types of vertices, as observed in Figure 1(b)(ii), one of which is the intersection of three faces (indicated by the black circle), and the other of which has four faces (yellow circle). This asymmetric feature leads to the destruction of the structure because of the natural tendency of the phase field model; however, the perfection of the structure prevents destruction from being initiated. The destructive process is simulated in the following section.
4.2. Deviation from Perfect Arrangement―Stability of the Structure
In the previous section, the nuclei were set on the perfect lattice points of a bcc or fcc arrangement, resulting in a completely regular structure. In this section, the initial nuclei are displaced from the perfect lattice points to demonstrate the stability of the structure. The deviation of each nucleus is determined using a random number within a sphere of radius Δrd.
Figure 2(a) shows the variation of the maximum and minimum cell sizes Gmax and Gmin for Δrd = 0.12 and 0.25 for the bcc arrangement, where the cell size is measured by the number of grids in each cell. In the early stage, every cell grows freely without any interruption, and all the cells have an identical volume. Some of the cells then collide with each other. In this duration, the growth rate is affected; some cells are accelerated, and others are delayed. Therefore, a deviation in the cell size is generated, and the difference between Gmax and Gmin becomes apparent. The difference in the cell size becomes larger as Δrd increases because the irregularity in the initial nuclei enhances the instability of the colliding cells. This type of instability is intensified in the usual phase-field model; small cells become smaller and absorbed by larger cells. In the present model, however, the volumetric balancing term f V in Equation (3) works efficiently, and all the cells converge to an average size.
Simultaneously, in this stage, the shape of each cell is relaxed such that every face is flattened, and sharp corners are blunted. Figure 2(b) shows the cell distribution for Δrd = 0.25, and two of the cells are selected and depicted in Figure 2(c). The cells are not complete truncated hexagons, as observed in Figure 1(a); however, the shape is mostly similar to them. In fact, the relaxation of the shape continues even though the volumetric growth is stopped, and the more complete shape will be obtained afterward.
Figure 3 presents the results for Δrd = 0.12 and 0.25 for the fcc arrangement. Similar to the case for bcc, a difference in the cell size is generated during the growth from the nuclei. The deviation is relatively larger, and the maximum cell size exceeds the average size given later. However, the overshoot is observed only temporarily, and all the cells settle shortly into an average size. Figure 3(b) and Figure 3(c) show the cell distribution and two individual selected cells, respectively. As observed in these figures, the cell shapes change drastically compared with the perfect rhombic dodecahedra presented in Figure 1(b), and the cells are more like truncated
![]() (a) (b) (c)
(a) (b) (c)
Figure 2. Variation of the maximum and minimum cell sizes, cell distribution in the whole simulation domain, and two typical cells selected from the model in the case that nuclei are set on deviated sites from complete bcc lattice points. (a) Variation of max. and min. cell size; (b) Cell distribution; (c) Typical cells.
hexagonal, as observed in Figure 2(c). The overshoot observed in the cell size variation in Figure 3(a) is then considered to be caused by the change in the morphology of the cells, and the extra time is needed for converging. The rhombic dodecahedra is considered a less stable structure than the truncated hexagonal; detailed analysis will be performed in future work.
4.3. Random Arrangement
Finally, nuclei are set on random sites to simulate cell growth under a more natural condition. The number of nuclei N is varied, and the cases for N = 16, 24, and 40 are presented in Figure 4.
Figure 4(a) shows the variation of the cell size for N = 24 and 40. In both cases, the variations are similar to those for the previous conditions shown in Figure 2 and Figure 3; the difference in cell size appears once but converges to a certain value because of the effect of the volumetric balancing term, and the deviation in cell size
![]() (a) (b) (c)
(a) (b) (c)
Figure 3. Variation of the maximum and minimum cell sizes, cell distribution in the whole simulation domain, and two typical cells selected from the model in the case that nuclei are set on deviated sites from complete fcc lattice points. (a) Variation of max. and min. cell size; (b) Cell distribution; (c) Typical cells.
![]()
Figure 4. Variation of the maximum and minimum cell sizes, evolution of the shape of a specific cell, and cell distribution of the whole domain at the 10000-th time step for the case where nuclei are set on random sites. (a) Variation of maximum and minimum cell size; (b) Varization of cell shape; (c) Cell distribution.
is more apparent in this case. Overshoots in the variation of cell size is more apparent for N = 40 because the spatial dispersion of the initial nuclei are more evident. A shoulder in Gmax curve for N = 24 is due to the largest cell is shifted. Figure 4(b) represents the variation of the shape of a specific cell after all the cells settle in a constant volume state for N = 16. The shape of the cell is distorted first; some faces are concave, and some vertices have sharp angles, as observed in Figure 4(b)(i). As time progresses, the faces are flattened, and vertices are blunted, resulting in a convex polyhedron by the 10,000-th time step, as observed in Figure 4(b)(iv). Figure 4(c)(i) and Figure 4(c)(ii) show the cell distribution for N = 24 and 40, respectively. In both cases, every cell is a convex polyhedron even though they are not completely identical. Further analysis on the cell shape and distribution will be presented in our future work.
5. Concluding Remarks
A phase field model for investigating the three-dimensional space-filling structures that were typically observed in metal foam materials was presented. An additional term to balance the volume of every cell was introduced to the conventional multi-phase field model, and the stability of the obtained structures was investigated. The truncated hexagonal structure, which is obtained by cell growth from nuclei arrangement on a bcc lattice, is more stable than the rhombic dodecahedron structure obtained from an fcc arrangement. In addition, when the nuclei are set on random sites, distorted cells are first generated; however, they settle into certain convex regular shapes of some type of polyhedron.
Further modeling is required for the detailed evaluation of the stability of the structures, such as physical interpretation of the volume constraint term introduced in the model. Presumably, this term can be explained by the consideration of the gaseous pressure in the cells. Fluidity during the cell growth process should strongly affect the morphology of the formed structure. These points will be addressed in our future work; however, it can be concluded that the availability of the model presented in this study is fairly validated.