Identification of Modal Loss Factor of a Sandwich Composite Structure with Polyethylene Terephthalate Core in the Aspect of Core Properties Determination ()
1. Introduction
Polyethylene terephthalate (PET) (C10H8O4)n is a thermoplastic polymer having various industrial applications. Due to the high mechanical strength and resistance to both low and high temperatures, PET films are often used in various structures as damping elements. To identify dynamic properties of thin film materials, a composite layered configuration is taken into investigations.
Scientific studies in the layered composite field are carried out for a long time. In the fifties of the twentieth century a method of damping of flexural vibration of the plate by means of viscoelastic laminate layers was presented by Ross et al. (1959). In sandwich configuration, the damping of the plate is caused by elongation and shear of viscoelastic layers. Theoretical and experimental analysis of the effectiveness of different configurations of viscoelastic damping layers was presented. The presented method, known in the literature as the RKU method was verified and used later in the works of many researchers (e.g. Jones, 2001 [2] ; Rao 2003 [3] , Martinez-Agirre and Elejabarrieta, 2010 [4] ).
The appearance at the end of the last century many new laminates caused interest in dynamics of layered composites with viscoelastic cores. To describe the viscoelastic properties of the core, both classical rheological models and fractional rheological models were used. For example in the study by Bagley and Torvik (1985) [5] three-layer beam with fractional internal damping is analyzed by using both a continuum formulation and a finite element formulation. In the later study by Cupiał and Nizioł (1995) [6] , three-layer plate with a viscoelastic middle layer is analyzed. To describe the viscoelastic properties of the core, a complex shear modulus determined from classical rheological models is used in this study. However, as shown in later studies in this field (e.g. Pritz (1996) [7] , Jones (2001) [2] , Marynowski (2012) [8] ), to describe the viscoelastic properties of laminated material it is necessary to introduce more accurate tool than the widely used classical rheological models.
The inaccuracy of the classical rheological models can be observed in the frequency domain, where the slope of the experimental amplitude curves is always smaller than that of the curves predicted by these models. The reason for this inaccuracy can be found in the stress-strain relationship defined in the time-domain by a linear differential equation of integer order. By replacing the integer order derivatives in the Zener rheological model with fractional order ones, the four-parameter rheological model with fractional derivatives was introduced in the studies by Pritz (1996, 2003) [7] [9] . The effect of the parameters on the frequency curves was demonstrated in these studies. It is shown that there is a strict relation between the dispersion of the dynamic modules, the loss peak and the slope of the frequency curves of the viscoelastic material. Since that time, the fractional model was used in many works (e.g. Beda and Chevalier 2004 [10] ; Cortes and Elejabarrieta 2006, 2007 [11] [12] ; De Espindola et al. 2008 [13] ; Monje et al. 2010 [14] ; Ghanbari and Haeri, 2011 [15] ). Overview of publications in this field, together with a critical analysis of, applications of fractional derivatives in modeling of mechanical systems, can be found, at the study of Rossikhin and Shitikova (2010) [16] .
A great variety of PET films, and also a trade secret hiding the full results of the research carried out by the manufacturers, make it necessary to conduct fundamental research in this field. In this study the authors focus attention on an important issue that arises in the identification of viscoelastic properties of thin polyethylene film. The three-layer sandwich structure consisting of a metal covers and the polyurethane core, is tested in the identification process. A method of determining of the loss factor of such composite object has a significant influence on the identification results of the polyethylene core. In the numerous papers many methods of the modal loss factor determination of viscoelastic structures may be found. These are mainly methods based on frequency bandwidth of the experimental resonant plot, but also methods based on other physical parameters. The latter categorizes the resonant amplitude method and the fit method of the response of a one degree of freedom model system to the measured response near a particular resonance peak. Authors determinated the impact of each method on the final identification results of polyethylene terephthalate (PET) material. The results in a quantitative manner set the applied methods and their practical utility in order.
2. The Effects of Temperature and Frequency
When a viscoelastic material is subjected to periodic load, the induced deformation is also periodic out of phase. Then the stress-strain relationship can be characterized by complex modulus given in the frequency domain, described in [2] , by
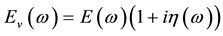 , (1)
, (1)
where 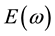 is the Young’s modulus, and
is the Young’s modulus, and 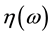 is the loss factor.
is the loss factor.
Assuming that Poisson ratio of the viscoelastic material is constant in frequency, the complex shear modules, yields
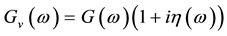 (2)
(2)
It is well known that most polymeric materials exhibit dynamic behavior which depends strongly on frequency and temperature. Polymers are composed of long intertwined and cross-linked molecular chains, each containing very many atoms. The internal molecular interactions which occur during vibration leads to energy dissipation and damping. If the polymers are homogenous and isotropic, the stiffness and damping characteristics vary with temperature and frequency. The shear, extensional and bulk moduli are closely related to each other for homogenous and isotropic polymers (Jones, 2001 [2] ).
The complex modules properties of polymers vary strongly with temperature, in ways particular to each polymer composition. Figure 1 illustrates nonlinear behavior of some typical polymers
Figure 1 shows that above softening temperature Ts in the transition region, the shear modulus decreases rapidly and the loss factor rises to a maximum in the temperature Tm and then falls again. In temperatures above the transition region, the modulus is low, and as the temperature continues to rise, the material disintegrates.
While the effects of frequency are small for typical metal solid materials, the effects of frequency is much stronger for many polymers. The effect of frequency is the inverse of the effect of temperature, increasing frequency is similar to the effect of decreasing temperature, but at much different rates, as Figure 2 illustrates. The difference is very significant. While the temperature may vary by a few hundred degrees to reach the transition region, the corresponding change of frequency encompass many orders of magnitude. In this range the frequency can vary from 10−8 Hz to 108 Hz or more. For low frequencies the loss factor and shear modulus increase slightly. In transition region one can observe strong increase of loss factor, which takes maximal value and then significantly decreases. In this region the shear modulus increases. Above the transient region one can notice further decrease of loss factor and slight increase of the shear modulus, which takes maximal value.
3. Fractional Rheological Model of Viscoelastic Material
It is known that fractional derivative rheological models constitute a powerful tool in describing the dynamic behavior of viscoelastic materials in the frequency and time domains (Pritz 1996 [7] , Jones 2001 [2] ). In order to reduce the number of terms required by the multiple-element models, the constitutive relation is represented in terms of non-integer order derivatives. The four-parameter fractional derivative model (generalized Zener model) is given by the formula presented in [2] :
![]()
Figure 1. Effect of temperature of complex modules behavior.
![]()
Figure 2. Effect of frequency of complex modules behavior.
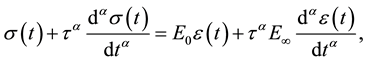 (3)
(3)
where: s―stress, e―strain, E0―static modulus, ―asymptotic modulus, t―relaxation time, α―fractional parameter (0 < α < 1).
―asymptotic modulus, t―relaxation time, α―fractional parameter (0 < α < 1).
On the base of the Fourier transform of Equation (3), the complex modulus is given by:
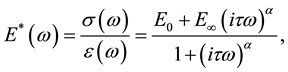 (4)
(4)
where: s(w)―the Fourier transform of s(t), e(w)―the Fourier transform of e(t), w―frequency, .
.
If the Poisson ratio of material is assumed to be constant in the considered frequency range, the complex shear modulus yields
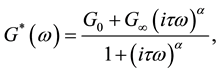 (5)
(5)
where: G0―static shear modulus,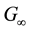 ―asymptotic shear modulus.
―asymptotic shear modulus.
Most often to identify the properties of viscoelastic material the sandwich composite structure with viscoelastic core is taken into experimental investigations. An experimental technique that allows identification of the complex modulus of the composite structure and the complex shear modulus of the viscoelastic core is utilized in this study.
4. Identification Method
A sandwich beam of the width b and the thickness (2h1 + h2) is considered. The top and bottom layers are made of the same elastic material and the core is of thin, soft polymeric material. The geometry and configuration of the layers are shown in Figure 3.
To identify and model the composite structure the Ross-Kerwin-Unger (RKU) equations are used (Ross et al., 1959 [17] ). The effect of bending of the viscoelastic core is neglected. Then the flexural rigidity of the composite cantilever beam according to [2] is given by
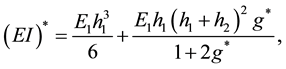 (6)
(6)
where:
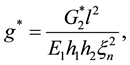 (7)
(7)
and: E1―Young’s modulus of the outer layer,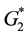 ―complex shear modulus of the core,
―complex shear modulus of the core,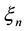 ―the n-th eigenvalue of the cantilever beam.
―the n-th eigenvalue of the cantilever beam.
In experimental way by applying a seismic excitation the flexural rigidity of the composite beam is determined. From the measured resonant frequencies and loss factors of the composite beam, and also from the response of outer beams taken separately, the modal flexural rigidity is given by the formula presented in [2] [4]
![]() , (8)
, (8)
![]()
Figure 3. Geometry and configuration of layers.
where: fn―the n-th resonant frequency of the composite beam, f0n―the n-th natural frequency of each individual outer beam, hn―the modal loss factor.
To measure the modal loss factor the standard ASTM E 746-2005 recommends the half-power bandwidth (HPB) method [1] . In this method from the experimental transmissibility function, the resonant frequency and the frequencies both above and below the resonant frequency are evaluated for each mode. These two frequencies are determined at points, where the value of the transmissibility function is 3.01 dB less than the value at resonance. Then the modal loss factor h is defined as the ratio of the half-power bandwidth ![]() to the resonant frequency f given by
to the resonant frequency f given by
![]() (9)
(9)
The HPB method is not the only method for determining the modal loss factor, described in the literature. In the same standard ASTM E 746-2005 the “n dB” bandwidth method is considered [1] . Then the modal loss factor is calculated by
![]() (10)
(10)
where![]() , and n the “n dB” value chosen from the range 0.5 - 3 dB.
, and n the “n dB” value chosen from the range 0.5 - 3 dB.
Is worth noting that the HPB method is the “n dB” bandwidth method when n = 3.01 dB. As in the HPB method, the frequencies above and below the resonant frequency are measured where the value of the experimental transmissibility function is n dB less than the value at resonance. In this study both the “2 dB” bandwidth method, and the “1 dB” bandwidth method are taken into considerations.
In addition to the methods of determining the loss factor utilizing the frequency bandwidth, in the literature can be found two other methods. One of them is a method in which to determine the loss factor is only necessary to measure the amplitudes of both the exciter and the test sample at resonance [7] . In the resonant amplitude method the loss factor is, according to [2] , given by
![]() (11)
(11)
where Xr is the measured amplitude ratio at resonance.
The second method, which does not use the frequency bandwidth, is the fit method of the response of a one degree of freedom model system to the measured response near to a particular resonance. In this method, the function of square error e, derived in [2] , determines the following expression:
![]() (12)
(12)
where: Xn―the nth measured displacement response amplitude at the frequency fn; fr―the resonant frequency; F―amplitude of the excitation force; k, h―stiffness and loss factors respectively of one degree of freedom model system.
On the base of the measured resonant frequencies and modal loss factors of the composite beam the identification of the core is possible. Comparing Equation (8) and Equation (6) the shear parameter![]() , closely related with the complex modal shear modulus of the core, according to [2] , can be determined
, closely related with the complex modal shear modulus of the core, according to [2] , can be determined
![]() . (13)
. (13)
From Equation (13) and Equation (7) the complex modal shear modulus of the core, shown in [2] , is given by
![]() , (14)
, (14)
where h2 is the modal loss factor of the core.
According to the standard ASTM E756-2005 [1] the shear modulus and the loss factor of the material of the core are derived by
![]() (15)
(15)
![]() (16)
(16)
where:
![]() ; (17)
; (17)
Cn―coefficient for the n mode of clamped―free beam.
5. Experimental Investigations
In order to determine loss factor of sandwich composite beam with viscoelastic core experimental investigations were carried out. Investigations were performed according to the standard ASTM E756-2005 [1] . A seismic excitation was generated by electrodynamic shaker Ling Dynamic System V780. For shaker signals parameters modification the signal generator HMF2525 was used. In Figure 4 the experimental configuration scheme is presented.
Specimens were mounted in the fixture on the shaker. Two laser streams from HSV-700 sensor head were directed respectively to fixture and free end of the beam in order to determine input and response signal. Signal was transmitted by optical fibers to two HSV-800 units and to HSV-2002 laser unit. Afterwards signal was transmitted via Brüel & Kjær Pulse to PC unit. In order to verify correctness of the signal oscilloscope was placed parallel to PC. Data was elaborated in LabShop software using Fast Fourier Transform. Furthermore as signal was measured as velocity it was necessary to perform integration in order to obtain displacement.
![]()
Figure 4. Test stand for investigation the loss factor of sandwich composite. 1―Arbitrary Generator HMF2525 Hameg Instruments, 2―Brüel & Kjær LDS HPA K amplifier, 3―LDS V780 shaker, 4―HSV-700 sensor head, 5―HSV-800, 6― HSV-2002 laser unit PC, 7―Brüel & Kjær Pulse, 8―oscilloscope, 9―PC, 10―specimen, 11―fixture.
In experimental studies the specimens in the form of the symmetric beams composed of two aluminum alloy PA38 with polyester-based adhesive core TESA4965 ware analyzed. In Figure 5 geometry of two specimens taken into investigations is shown. Properties of the core and layers materials are presented respectively in tables Table 1 and Table 2.
During the tests investigations single base beams and composite beams were tested as was mentioned in [4] . Six specimens were subjected to the pink noise input signal. In order to determine the resonant plot the Fast Fourier Transformation (FFT) of the response signal was used. Afterwards the specimens (length of the beams l = 180 mm and l = 250 mm) were subjected to sinusoidal excitations with frequencies in the vicinity of each resonant frequency. In this way the five resonant frequencies of the single base beams and the composite beams were identified. The value of the loss factor of sandwich composite beam with viscoelastic core was determined according to the “3 dB”, “2 dB”, “1 dB” bandwidth methods, the resonant amplitude method and the fit method.
Investigation Results
Investigation results for samples for the free length of the beam l = 250 mm and l = 180 mm were presented respectively in Table 3 and Table 4.
Samples of the length l = 180 mm (corresponding to the shortest length recommended by the standard) was subjected investigation to more accurately determine the position of the high frequency asymptote of the core material characteristic. The calculation results of the sandwich beams loss factor presented in tables Table 3 and Table 4 are shown respectively on plots in Figure 6 and Figure 7.
![]()
Table 1. Properties of the material TESA4965.
![]()
Table 2. Material properties of the alloy PA38/6060.
![]()
Table 3. Sandwich composite beam loss factor comparison for the free length of the beam l = 250 mm.
![]()
Table 4. Sandwich composite beam loss factor comparison for free length of the beam l = 180 mm.
![]()
Figure 6. Graphical comparison of the loss factor values for the sandwich composite beam for the free length of the beam l = 250 mm.
![]()
Figure 7. Graphical comparison of the loss factor values for the sandwich composite beam for the free length of the beam l = 180 mm.
6. Core Properties Identification
Data obtained according to the particular methods of the sandwich beam loss factor determination was used in further calculations. According to the standard ASTM E756-2005 [1] shear modulus and loss factor of the core material are described by the formulas (15) and (16). It shows that both shear modulus and loss factor of viscoelastic core material depends on the loss factor of whole composite structure. Using loss factor calculations results, presented in the previous section, the identification of rheological parameters of fractional model of the core material was carried out. To determine the function of the complex shear modulus of the core material, the Nelder-Mead method was applied. Formulas for the different methods of loss factor determination of the composite material were obtained. Identification results are shown in Figures 8-12.
The results presented in Figures 8-12 show that the “3 dB”, “2 dB”, “1 dB” methods and the fit method provides similar results for the core material rheological parameters identification. Identification results by mean of the resonant amplitude method significantly differ from the others. The plot of shear modulus is characterized by the greatest value of the slope for the transition region (α = 0.834). The values of fractional parameter α obtained from other methods are within range: α = 0.626 (“3 dB” method) to α = 0.7 (“1 dB” method). Also the maximal loss factor value for the resonance amplitude method is twice as high as results obtained according to other four methods.
In Figure 13 identification results comparison is presented. Shear modulus and the loss factor as a function of frequency are shown. Shear modulus low frequency asymptote values are close to each other for the bandwidth methods and the fit method (range from G0 = 1.947 MPa for the fit method to G0 = 2.01 MPa―for “1 dB” method). Shear modulus high frequency asymptote values are within range from G∞ = 4.9 MPa (“3 dB” method) to G∞ = 4.97 MPa (“1 dB” method). Loss factor maximal value for “n dB” and fit methods is observed for the range from η = 0.819 (the “3 dB” method) to η = 0.977 (the “1 dB” method). The relaxation time τ is related to the frequency at which the loss factor is maximum, is the lowest value for the ’’3 dB” method (τ = 0.18 × 10−4), and minimum for the “1 dB” method (τ = 0.24 × 10−4).
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 8. Rheological parameters identification for the “3 dB” method.
![]() (a)
(a) ![]() (b)
(b)![]() (c)
(c)
Figure 9. Rheological parameters identification for the “2 dB” method.
![]() (a)
(a) ![]() (b)
(b)![]() (c)
(c)
Figure 10. Rheological parameters identification for the “1 dB” method.
![]() (a)
(a) ![]() (b)
(b)![]() (c)
(c)
Figure 11. Rheological parameters identification for the fit method.
![]() (a)
(a) ![]() (b)
(b)![]() (c)
(c)
Figure 12. Rheological parameters identification for the resonant amplitude method.
![]()
Figure 13. Comparison of identification results.
7. Conclusions
Comparison of the loss factor determination of the sandwich composite methods with polyethylene core results in the identification of the fractional rheological model of the core material is presented in this study. Five methods of the loss factor determination of the three layer composite with viscoelastic core were compared. Three of the compared methods are bandwidth methods, and the other two the resonant amplitude method and the fit method. Identified material was polyethylene terephthalate (PET) used as a thin film placed between two covers made of an aluminum alloy. Applied identification procedure in accordance with ASTM E756-2005 [17] , is based on experimental studies of forced vibrations of such composite structure. The paper becomes convenient practical guide describing the main advantages and disadvantages and detailed methodology for composite loss factor determination.
For the bandwidth methods and the fit method, convergence of identified values of rheological parameters is obtained. The obtained results by means of the resonance amplitude method differ significantly from the others. Different physical nature of the data, used to determine the loss factor of the sandwich beam, causes the difference. For the amplitude method, only the amplitude of the exciter and the beam at resonance peak is measured. The methods of the loss factor determination by means of the frequency bandwidth, are determined by the graph of the function in close proximity to the resonance peak. Similar features present the fit method: experimental data are matched to the response of a one degree of freedom system. Taking into account the graph of the function in the vicinity of resonance peak the modal loss factor can be determined more precisely. According to received results one can conclude that only the bandwidth methods and the fit method in the identification procedure allow obtaining correct results of identification of polyethylene material.
Identification results obtained by means of the “3 dB” method and the fit method are close to each other. Due to the fact that the “3 dB” method is easier and more convenient to use than the fit method, it is common recommended in engineer practice, and is the most frequently used method for the loss factor determination of viscoelastic layer composites. However, due to the flattening of the resonance peaks appearing at the higher modes of vibration, often the “3 dB” method cannot be used. Then the “n dB” bandwidth methods may be used. The results of identification by mean of the “2 dB” and “1 dB” bandwidth methods have proved the correctness of such proceedings.
NOTES
*Corresponding author.