Extended Diagonal Exponent Symmetry Model and Its Orthogonal Decomposition in Square Contingency Tables with Ordered Categories ()
1. Introduction
Consider an 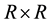 square contingency table with the same row and column classifications. Let
square contingency table with the same row and column classifications. Let  denote the probability that an observation will fall in the ith row and jth column of the table
denote the probability that an observation will fall in the ith row and jth column of the table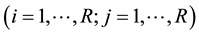 . The symmetry (S) model is defined by
. The symmetry (S) model is defined by

where 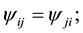 see Bowker [2] . Caussinus [3] considered the quasi-symmetry (QS) model defined by
see Bowker [2] . Caussinus [3] considered the quasi-symmetry (QS) model defined by

where  The marginal homogeneity (MH) model is defined by
The marginal homogeneity (MH) model is defined by

where 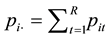 and
and 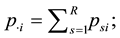 see Stuart [4] . Caussinus [3] gave the theorem that the S model holds if and only if both the QS and MH models hold.
see Stuart [4] . Caussinus [3] gave the theorem that the S model holds if and only if both the QS and MH models hold.
Tomizawa [1] considered the diagonal exponent symmetry (DES) model defined by
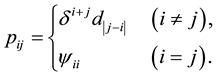
By putting  and
and 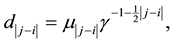 this model is also expressed as
this model is also expressed as
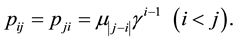
Note that the DES model implies the S model; thus the DES model implies the QS (MH) model. The DES model states that 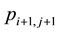
 is
is ![]() times higher than
times higher than![]() ; in other words, for fixed distance k
; in other words, for fixed distance k ![]() from the main diagonal of the table,
from the main diagonal of the table, ![]() increase (decrease) exponentially along every subdiagonal of the table as the value i increase
increase (decrease) exponentially along every subdiagonal of the table as the value i increase![]() .
.
Iki, Yamamoto and Tomizawa [5] considered the quasi-diagonal exponent symmetry (QDES) model defined by
![]()
A special case of the QDES model obtained by putting ![]() is the DES model. Note that the QDES model implies the QS model. Let X and Y denote the row and column variables, respectively. We define the mean equality (ME) model as
is the DES model. Note that the QDES model implies the QS model. Let X and Y denote the row and column variables, respectively. We define the mean equality (ME) model as![]() . Iki et al. [5] gave the theorem that the DES model holds if and only if both the QDES and ME models hold.
. Iki et al. [5] gave the theorem that the DES model holds if and only if both the QDES and ME models hold.
Iki et al. [5] described the relationship between the QDES model and a joint bivariate normal distribution, and showed that the QDES model may be appropriate for a square ordinal table if it is reasonable to assume an underlying bivariate normal distribution with equal marginal variances. We are interested in considering the new model which is appropriate for a square ordinal table if it is reasonable to assume an underlying bivariate normal distribution without equal marginal variances, and a decomposition using the proposed models.
The present paper proposes two models, and gives the decomposition using the proposed models. Also it shows the orthogonality of the test statistics for decomposed model.
2. New Models
Consider a model defined by
![]()
A special case of this model obtained by putting ![]() is the DES model. Thus we shall refer to this model as the extended diagonal exponent symmetry (EDES) model. The EDES model states that
is the DES model. Thus we shall refer to this model as the extended diagonal exponent symmetry (EDES) model. The EDES model states that ![]()
![]() is
is ![]() times higher than
times higher than![]() ; in other words, for fixed distance from the main diagonal of the table, the ratio of
; in other words, for fixed distance from the main diagonal of the table, the ratio of ![]() to
to ![]() increases (decreases) exponentially along every subdiagonal of the table. Note that the EDES model implies the S model.
increases (decreases) exponentially along every subdiagonal of the table. Note that the EDES model implies the S model.
Next, consider a model defined by
![]()
A special case of this model obtained by putting ![]() is the QDES model. Thus we shall refer to this model as the extended quasi-diagonal exponent symmetry (EQDES) model. A special case of the EQDES model obtained by putting
is the QDES model. Thus we shall refer to this model as the extended quasi-diagonal exponent symmetry (EQDES) model. A special case of the EQDES model obtained by putting ![]() and
and ![]() is the EDES model. The EQDES model states that
is the EDES model. The EQDES model states that ![]()
![]() is
is ![]() times higher than
times higher than![]() ; in other words, for fixed distance from the main diagonal of the table, the ratio of
; in other words, for fixed distance from the main diagonal of the table, the ratio of ![]() to
to ![]() increases (decreases) exponentially along every subdiagonal of the table. Note that the EQDES model implies the QS model.
increases (decreases) exponentially along every subdiagonal of the table. Note that the EQDES model implies the QS model.
Under the EQDES model, we can see
![]()
where![]() . This indicates that the odds that an observation will fall in the
. This indicates that the odds that an observation will fall in the ![]() th cell, instead of the
th cell, instead of the ![]() th cell is
th cell is ![]() times higher than the odds that the observation will fall in the
times higher than the odds that the observation will fall in the ![]() th cell, instead of the
th cell, instead of the ![]() th cell. Also we can see
th cell. Also we can see
![]()
where ![]() and
and![]() . If
. If![]() , for corresponding i and j, the structure of
, for corresponding i and j, the structure of ![]() holds. Also if
holds. Also if![]() , the structure of
, the structure of ![]() holds.
holds.
In Figure 1, we show the relationships among models. In figure, ![]() indicates that model A implies model B.
indicates that model A implies model B.
3. Decomposition
Refer to model of equality of marginal means and variances, i.e., ![]() and
and ![]() as the MVE model. This model is also expressed as
as the MVE model. This model is also expressed as ![]() and
and ![]() We obtain the decomposition of the EDES model as follows:
We obtain the decomposition of the EDES model as follows:
Theorem 1. The EDES model holds if and only if the EQDES and MVE models hold.
Proof. If the EDES model holds, then the EQDES and MVE models hold. Assuming that both the EQDES and MVE models hold, then we shall show that the EDES model holds. Let ![]() denote the cell probabilities which satisfy both the EQDES and MVE models. Since the EQDES model holds, we see
denote the cell probabilities which satisfy both the EQDES and MVE models. Since the EQDES model holds, we see
![]() (1)
(1)
Let ![]() with
with ![]() We denote that
We denote that ![]() with
with ![]() Then, since
Then, since ![]() satisfy the EQDES and MVE models, we see
satisfy the EQDES and MVE models, we see
![]() (2)
(2)
and
![]() (3)
(3)
where ![]()
![]()
![]()
![]() with
with ![]() and
and![]() .
.
Then, we denote ![]() by
by ![]() and
and ![]() by
by ![]()
Consider the arbitrary cell probabilities ![]() satisfying
satisfying
![]() (4)
(4)
where ![]()
![]()
![]() and
and ![]()
From (2), (3) and (4), we see
![]() (5)
(5)
Using the Equation (5), we obtain
![]()
where
![]()
and ![]() is the Kullback-Leibler information between
is the Kullback-Leibler information between ![]() and
and![]() . Since
. Since ![]() being a func-
being a func-
tion of ![]() is fixed, we see
is fixed, we see
![]()
and then ![]() uniquely minimizes
uniquely minimizes ![]() (see Bhapkar and Darroch [6] ).
(see Bhapkar and Darroch [6] ).
Let ![]() for
for ![]() Then
Then
![]() (6)
(6)
Noting that ![]() the Equation (6) is also expressed as
the Equation (6) is also expressed as
![]() (7)
(7)
From (3), (4) and (7), we see
![]() (8)
(8)
Using the Equation (8), we obtain
![]()
Since ![]() being a function of
being a function of ![]() is fixed, we see
is fixed, we see
![]()
and then ![]() uniquely minimizes
uniquely minimizes ![]() Therefore, we see
Therefore, we see ![]() Thus,
Thus, ![]()
From (1) and (6), for![]() , we see
, we see
![]()
Thus, we obtain ![]() and
and ![]() Namely, the EDES model holds. The proof is completed.
Namely, the EDES model holds. The proof is completed.
4. Orthogonality of Test Statistics
Let nij denote the observed frequency in the (i, j)th cell of the table ![]() with
with![]() , and let
, and let ![]() denote the corresponding expected frequency. Assume that
denote the corresponding expected frequency. Assume that ![]() have a multinomial distribution. The maximum likelihood estimates (MLEs) of
have a multinomial distribution. The maximum likelihood estimates (MLEs) of ![]() under the EDES and EQDES models could be obtained using iterative procedures; for example, see Darroch and Ratcliff [7] . The MLEs of
under the EDES and EQDES models could be obtained using iterative procedures; for example, see Darroch and Ratcliff [7] . The MLEs of ![]() under the MVE model could be obtained using Newton-Raphson method to the log-likelihood equations.
under the MVE model could be obtained using Newton-Raphson method to the log-likelihood equations.
Let ![]() denote the likelihood ratio chi-squared statistic for testing goodness-of-fit model M. The numbers of degrees of freedom (df) for the EDES and EQDES models are
denote the likelihood ratio chi-squared statistic for testing goodness-of-fit model M. The numbers of degrees of freedom (df) for the EDES and EQDES models are ![]() and
and![]() , respectively.
, respectively.
The orthogonality (asymptotic separability or independence) of the test statistics for goodness-of-fit of two models is discussed by, e.g., Darroch and Silvey [8] and Read [9] . We obtain as follow:
Theorem 2. The test statistic ![]() is asymptotically equivalent to the sum of
is asymptotically equivalent to the sum of ![]() and
and![]() .
.
Proof. The EQDES model is expressed as
![]() (9)
(9)
where ![]() Let
Let
![]()
where “t” denotes the transpose, and
![]()
is the ![]() vector. The EQDES model is expressed as
vector. The EQDES model is expressed as
![]()
where X is the ![]() matrix with
matrix with ![]()
![]() (the R2 × 1 vector),
(the R2 × 1 vector), ![]() (the R2 × 1 vector),
(the R2 × 1 vector), ![]() (the R2 × 1 vector),
(the R2 × 1 vector), ![]() (the R2 × 1 vector), and
(the R2 × 1 vector), and ![]() is the
is the ![]() matrix of 1 or 0 elements determined from (9),
matrix of 1 or 0 elements determined from (9), ![]() is the
is the ![]() vector of 1 elements,
vector of 1 elements, ![]()
![]() and
and ![]() denotes the Kronecker product. The matrix X is full column rank which is K. In a similar manner to Haber [10] , we denote the linear space spanned by the columns of the matrix X by
denotes the Kronecker product. The matrix X is full column rank which is K. In a similar manner to Haber [10] , we denote the linear space spanned by the columns of the matrix X by ![]() with the dimension K.
with the dimension K.
Let U be an![]() , where
, where![]() , full column rank matrix such that
, full column rank matrix such that ![]() is the orthogonal complement of
is the orthogonal complement of![]() . Thus,
. Thus, ![]() , where
, where ![]() is the s × t zero matrix. Therefore the EQDES model is expressed as
is the s × t zero matrix. Therefore the EQDES model is expressed as
![]()
where ![]() is the
is the ![]() zero vector, and
zero vector, and![]() . The MVE model is expressed as
. The MVE model is expressed as
![]()
where![]() , and
, and![]() , with
, with ![]() being the
being the ![]() matrix. Namely,
matrix. Namely,![]() . Thus
. Thus ![]() belongs to
belongs to ![]() Hence
Hence ![]() From Theorem 1, the EDES model is expressed as
From Theorem 1, the EDES model is expressed as
![]()
where ![]() and
and![]() .
.
Let ![]() denote the
denote the ![]() matrix of partial derivative of
matrix of partial derivative of ![]() with respect to p, i.e.,
with respect to p, i.e., ![]() Let
Let![]() , where
, where ![]() denotes a diagonal matrix with ith component of p as ith diagonal component. Let
denotes a diagonal matrix with ith component of p as ith diagonal component. Let ![]() denote p with
denote p with ![]() replaced by
replaced by![]() . Then
. Then ![]() has asymptotically a normal distribution with mean
has asymptotically a normal distribution with mean ![]() and covariance matrix
and covariance matrix![]() . Using the delta method,
. Using the delta method, ![]() has asymptotically a normal distribution with mean
has asymptotically a normal distribution with mean ![]() and covariance matrix
and covariance matrix
![]()
Note that ![]() belongs to
belongs to ![]() because
because![]() . Thus
. Thus![]() . Since
. Since
![]() and
and![]() , we see
, we see
![]()
Thus, we obtain ![]() where
where
![]() (10)
(10)
Under each![]() , the Wald statistic
, the Wald statistic ![]() has asymptotically a chi-squared distribution with
has asymptotically a chi-squared distribution with ![]() degrees of freedom. From (10), we see that
degrees of freedom. From (10), we see that ![]() From the asymptotic equivalence of the Wald statistic and likelihood ratio statistic, we obtain Theorem 2.
From the asymptotic equivalence of the Wald statistic and likelihood ratio statistic, we obtain Theorem 2.
5. Examples
Example 1. Consider the data in Table 1, taken from Bishop, Fienberg and Holland [11] , which describe the cross-classification of father’s and son’s occupational status categories in Denmark. The row is the father’s status category and column is the son’s status category. The categories are ordered from (1) to (5) (high to low). These data have also been analyzed by some statisticians; see for example, Kullback [12] , Haberman [13] , Goodman [14] , and Yamamoto, Tahata and Tomizawa [15] .
![]()
Table 1. Occupational status for Danish father-son pairs; from Bishop et al. [11] . (The parenthesized values are MLEs of expected frequencies under the EQDES model.)
Note: Status (1) is high professionals, (2) white-collar employees of higher education, (3) white-collar employees of less high education, (4) upper working class, and (5) unskilled workers.
We see from Table 3 that the EQDES and QS models fit these data well, although the other models fit poorly. The EQDES model is a special case of the QS model. We shall test the hypothesis that the EQDES model holds assuming that the QS model holds for these data. Since ![]() with 6 df being the difference between the numbers of df for the EQDES and the QS models, this hypothesis is accepted at the 0.05 significance level. Therefore, the EQDES model would be preferable to the QS model.
with 6 df being the difference between the numbers of df for the EQDES and the QS models, this hypothesis is accepted at the 0.05 significance level. Therefore, the EQDES model would be preferable to the QS model.
Under the EQDES model, the MLEs of ![]()
![]()
![]() and
and ![]() are
are ![]()
![]()
![]() and
and ![]() respectively. Therefore the probability that a father’s and his son’s status categories are
respectively. Therefore the probability that a father’s and his son’s status categories are ![]() and
and![]() , respectively, is estimated to be
, respectively, is estimated to be ![]() times higher than the probability that those are i and j, respectively
times higher than the probability that those are i and j, respectively![]() . Since the values of
. Since the values of ![]() for
for ![]() and
and ![]() are greater than 1 and it for
are greater than 1 and it for ![]() is less than 1 (see Table 2), the probability that a father’s and his son’s status categories are
is less than 1 (see Table 2), the probability that a father’s and his son’s status categories are ![]() and
and![]() , respectively, is estimated to be greater than the probability that those are i and j, respectively
, respectively, is estimated to be greater than the probability that those are i and j, respectively![]() .
.
Also the MLEs of ![]()
![]() are
are![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
and![]() , respectively. Therefore, it is estimated that there is the structure of
, respectively. Therefore, it is estimated that there is the structure of ![]() for
for ![]() with
with ![]() and
and ![]() for
for ![]() with
with ![]() and 4.
and 4.
We see from Table 3 that the poor fit of the EDES model is caused by the influence of the lack of structure of the MVE model rather than the EQDES model.
Example 2. Consider the data in Table 4 taken from Tomizawa [16] . These data are an unaided distance vision of 3168 pupils comprising nearly equal number of boys and girls aged 6 - 12 at elementary schools in Tokyo, Japan, examined in June 1984. These data have also been analyzed by Tomizawa [1] , Tahata and Tomizawa [17] , and Iki et al. [5] . The row is the right eye grade and column is the left eye grade.
We see from Table 3 that the EDES and EQDES models fit these data well, although the MVE model fits poorly. The EDES model is a special case of the EQDES model. We shall test the hypothesis that the EDES
![]()
Table 2. Values of![]() ,
, ![]() , under the EQDES model applied to Table 1.
, under the EQDES model applied to Table 1.
![]()
Table 3. Likelihood ratio chi-squared values ![]() for models applied to Table 1 and Table 4.
for models applied to Table 1 and Table 4.
*means significant at the 0.05 level.
model holds assuming that the EQDES model holds for these data. Since
![]()
with 2 df being the difference between the numbers of df for the EDES and the EQDES models, this hypothesis is rejected at the 0.05 significance level. Therefore, the EQDES model would be preferable to the EDES model.
Under the EQDES model, the MLEs of ![]()
![]()
![]() and
and ![]() are
are ![]()
![]()
![]() and
and ![]() respectively. Therefore the probability that a pupil’s right eye grade and his or her left eye grade are
respectively. Therefore the probability that a pupil’s right eye grade and his or her left eye grade are ![]() and
and![]() , respectively, is estimated to be
, respectively, is estimated to be ![]() times higher than the probability that those are i and j, respectively
times higher than the probability that those are i and j, respectively![]() . Since all values of
. Since all values of![]() ,
, ![]() , are less than 1 (see Table 5), the probability that a pupil’s right eye grade and his or her left eye grade are
, are less than 1 (see Table 5), the probability that a pupil’s right eye grade and his or her left eye grade are ![]() and
and![]() , respectively, is estimated to be less than the probability that those are i and j, respectively
, respectively, is estimated to be less than the probability that those are i and j, respectively![]() .
.
Also the MLEs of ![]()
![]() are
are![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() , respectively. Therefore, it is estimated that there is the structure of
, respectively. Therefore, it is estimated that there is the structure of ![]() for
for ![]() with
with ![]() and 4 and
and 4 and ![]() for
for ![]() with
with ![]() and 7.
and 7.
6. Simulation Studies
Under the QDES model, we see the structure of ![]() which is the structure of Agresti’s [18]
which is the structure of Agresti’s [18]
![]()
Table 4. Unaided distance vision of 3168 pupils comprising nearly equal number of boys and girls aged 6 - 12 at elementary schools in Tokyo, Japan, examined in June 1984; from Tomizawa [16] . (Upper and lower parenthesized values are MLEs of expected frequencies under the EDES and EQDES models, respectively.)
![]()
Table 5. Values of![]() ,
, ![]() , under the EQDES model applied to Table 4.
, under the EQDES model applied to Table 4.
linear diagonals-parameter symmetry model, and under the EQDES model, we see the structure of ![]() which is the structure of Tomizawa’s [19] extended linear diagonals-parameter symmetry model. Also under the DES and EDES models, we see the structure of
which is the structure of Tomizawa’s [19] extended linear diagonals-parameter symmetry model. Also under the DES and EDES models, we see the structure of ![]() for
for![]() .
.
Consider now random variables U and V having a joint bivariate normal distribution with means ![]() and
and ![]() variances
variances ![]() and
and ![]() and correlation
and correlation ![]() Then the joint bivariate normal density function
Then the joint bivariate normal density function ![]() satisfies
satisfies
![]()
Namely, ![]() has the form
has the form ![]() for constant
for constant ![]() and
and![]() . Agresti [18] described relationship between the linear diagonals-parameter symmetry model and the joint bivariate normal distribution (see also Tomizawa [19] ). We now consider the relationship between the QDES (DES) and EQDES (EDES) models and the joint bivariate normal distribution in terms of simulation studies.
. Agresti [18] described relationship between the linear diagonals-parameter symmetry model and the joint bivariate normal distribution (see also Tomizawa [19] ). We now consider the relationship between the QDES (DES) and EQDES (EDES) models and the joint bivariate normal distribution in terms of simulation studies.
Table 6 gives the ![]() tables of sample size 5000 formed by using cut points for each variable at
tables of sample size 5000 formed by using cut points for each variable at![]() ,
, ![]() , for underlying bivariate normal distribution with the conditions
, for underlying bivariate normal distribution with the conditions![]() , and
, and ![]() and
and![]() (Table 6(a)),
(Table 6(a)), ![]() and
and ![]() (Table 6(b)),
(Table 6(b)), ![]() and
and ![]() (Table 6(c)) and
(Table 6(c)) and ![]() and
and ![]() (Table 6(d)).
(Table 6(d)).
(c) ![]()
(d) ![]()
![]()
Table 7. Likelihood ratio chi-squared values ![]() for models applied to Tables 6(a)-6(d).
for models applied to Tables 6(a)-6(d).
*means significant at the 0.05 level.
We see from Table 7 that the EQDES model fits well for each of Tables 6(a)-6(d), although the QDES model fits well for each of Table 6(a) and Table 6(b), and fits poorly for each of Table 6(c) and Table 6(d). The DES and EDES models fit well for Table 6(a) and fit poorly for each of Tables 6(b)-6(d). Thus the EQDES model may be appropriate for a square ordinal table if it is reasonable to assume an underlying bivariate normal distribution (without the equality of marginal variances), although the QDES model may be appropriate if it is reasonable to assume it with equal marginal variances, and the DES and EDES models may be appropriate if it is reasonable to assume it with both equal marginal means and equal marginal variances.
7. Concluding Remarks
Theorem 1 may be useful for seeing the reason for the poor fit when the EDES model fits the data poorly; in fact, see from Example 1, a poor fit of the EDES model would be caused by a poor fit of the MVE model rather than the EQDES model.
From Theorem 2, we point out that the ![]() can be easily calculated using the
can be easily calculated using the ![]() and
and![]() ; in fact, see from Table 3, the value of
; in fact, see from Table 3, the value of ![]() is very close to the value of the sum of
is very close to the value of the sum of ![]() and
and ![]()
From Simulation studies, the EQDES model may be appropriate for a square ordinal table if it is reasonable to assume an underlying bivariate normal distribution without equal marginal means and equal marginal variances; although the QDES model may be appropriate if it is reasonable to assume it with equal marginal variances.
Acknowledgements
The authors would like to thank the editor and the referee for theirhelpful comments.