Nonlinear Free Vibrations of C-C-SS-SS Symmetrically Laminated Carbon Fiber Reinforced Plastic (CFRP) Rectangular Composite Plates ()
1. Introduction
The geometrically nonlinear vibration of structures is of continuing interest, due to the tendency to build more reliable structures, with high strength, high stiffness, and low weight such as composites. Such new materials have a more accentuated nonlinear behavior [1] - [6] . It is then necessary to develop new design concepts, taking into account the nonlinear behavior induced by large vibration amplitudes, which may occur for example in severe environments. The large displacement amplitudes induce geometrical nonlinearity that is mainly caused by the development of in-plane membrane stresses. In such cases, one of the basic assumptions of the linear vibration theory, i.e. small displacement amplitudes compared to the plate thickness is violated. Therefore, it is of crucial theoretical and practical interest, to develop new approaches which take into account the membrane stress effect, neglected in the classical treatment of plate vibrations. Even though the vibration of plates overall has interested researchers for a long time, the exact linear solutions are known only for the six cases having two opposite edges simply supported corresponding to a square plate or a rectangular plate [7] [8] . Also, as has been mentioned in the study made by Leissa in 1973 [7] , it was pointed out that until 1954, when Warburton derived his formulae based on a single-term representation of the deflection shapes for the natural frequencies of plates with various boundary conditions, no solution, even approximate, was known for six boundary condition cases. The general accuracy of Warburton’s formulae is discussed in references [7] [8] .
A great deal of studies and a wide program of experimental work carried out by White and his co-workers [9] - [18] has been developed in order to understand the dynamic behavior of homogeneous and CFRP beams and plates. In Chia’s book [19] , an extensive information is given on the nonlinear analysis of plates, with presentation of a variety of geometrically nonlinear static and dynamic problems. Also, a survey was presented of the literature on the geometrical nonlinear analysis of laminated composite elastic plates in reference [20] . In Sathyamoorthy’s work [21] , a review was presented which deals with analytical, numerical and experimental methods used in the geometrically nonlinear dynamic analysis of plates.
In recent works carried out by F. Alijani and M. Amabili [22] [23] in 2013, nonlinear vibrations of completely free laminated and sandwich rectangular plates are investigated using a multi-modal energy approach based on Lagrange equations and by using classical and higher-order shear deformation theories [24] with von Karman type nonlinearities [25] .
In several engineering applications, large vibration amplitudes of plate-type structures are encountered especially in the aerospace sector. The plates are assumed to be whether fully or partially free, simply supported, or clamped. The clamped boundary conditions assume that both displacements and rotations are prevented. In exchange, the simply supported boundary conditions assume that displacements are allowed, but rotations are not. In practice, it is extremely hard to achieve both cases [26] , because the real plate boundaries are neither completely clamped nor simply supported. So, in most cases, the real boundary conditions are a combination of clamped, simply supported, or free conditions. As a real illustrative example of the combination of the boundary conditions, aircraft wing panels may be mentioned [27] .
The purpose of this paper is to apply the theoretical model developed in references [1] - [3] in order to analyze the geometrically nonlinear free dynamic response of C-C-SS-SS rectangular CFRP symmetrically laminated plates so as to investigate the effect of nonlinearity on the nonlinear resonance frequencies, the nonlinear funda- mental mode shape and associated bending stress patterns at large vibration amplitudes. Various values of the plate aspect ratio and the amplitude of vibration will be considered, and useful numerical data will be provided.
2. General Formulation of the Geometrically Nonlinear Free Vibration of C-C-SS-SS Symmetrically Laminated Rectangular Composite Plates
2.1. Constitutive Equation at Large Deflections
Consider the transverse vibration W of the plate of dimensions a, b and H shown in Figure 1 with a coordinate system taken such that the xy plane coincides with the mid-plane of the plate.
The strain-displacement relationships for large deflections, considering the classical plate laminated theory [28] , are given by the expressions taken from reference [29] which assume that (a) the plate is thin (the thickness H is much smaller than the typical plate dimension, H << a, b), (b) the magnitude of the transverse deflection
W is of the same order as the thickness of the plate, and (c) the in-plane displacements U and V are linear functions of the z-coordinate:
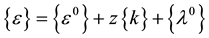 . (1)
. (1)
where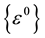 ,
, 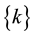 and
and 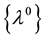 are given by [1] -[5] :
are given by [1] -[5] :
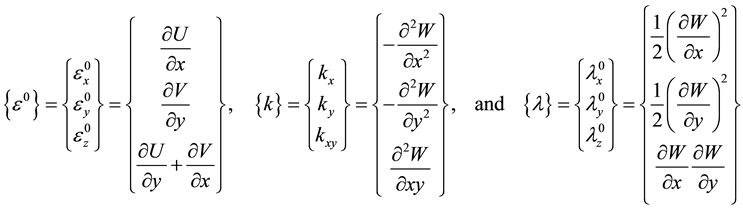 (2)(3)(4)
(2)(3)(4)
where U, V, and W are the displacements of the plate mid-plane, in the x, y and z directions respectively. In the development of the nonlinear energy expression, the transverse displacement W of the plate mid-plane has been taken into consideration while the in-plane displacements U and V have been neglected. Therefore, the strain energy (5, 6) of an elastic solid is written in Cartesian coordinates as follows [1] - [5] :
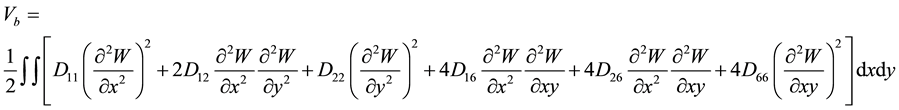 (5)
(5)
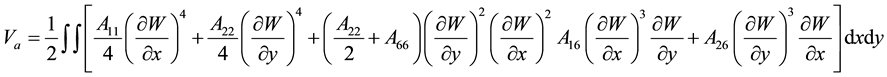 (6)
(6)
The kinetic energy of the plate may be written as [1] - [5] :
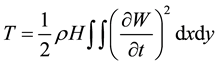 (7)
(7)
In which the in-plane and rotary inertia terms are neglected.
2.2. Numerical Model for the Nonlinear Mode Shapes and Resonance Frequencies of C-C-SS-SS Rectangular CFRP Symmetrically Laminated Plates
The transverse displacement function W may be written as in references [29] [30] in the form of a double series as follows:
 (8)
(8)
where ij is the contribution coefficient of the function obtained as product of the ith clamped simply-supported beam mode shape in the x-direction, with the jth clamped simply-supported beam mode shape in the y-direction for the case of C-C-SS-SS rectangular plates, and vice versa.
The discretization of the strain and kinetic energy expressions (5)-(7) can be carried out leading to [1] - [5] :
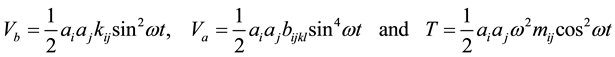 (9)(10)(11)
(9)(10)(11)
where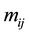 ,
, 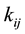 , and
, and 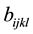 are respectively the mass tensor, the rigidity tensor and the geometrical nonlinearity tensor. These tensors are related to the corresponding nondimensional ones by:
are respectively the mass tensor, the rigidity tensor and the geometrical nonlinearity tensor. These tensors are related to the corresponding nondimensional ones by:
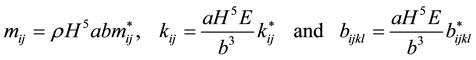 (12)(13)(14)
(12)(13)(14)
where the nondimensional tensors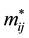 ,
, ![]() , and
, and ![]() have the below form:
have the below form:
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
Applying Hamilton’s principle to the vibration problem gives:
![]() (18)
(18)
In matrix form, the above expression (18) may be rewritten as:
![]() (19)
(19)
where ![]() is the nondimensional nonlinear frequency parameter, the expression of which can be obtained by pre-multiplying Equation (18) by
is the nondimensional nonlinear frequency parameter, the expression of which can be obtained by pre-multiplying Equation (18) by ![]() from the left-hand side, which leads to the following equation:
from the left-hand side, which leads to the following equation:
![]() (20)
(20)
The set of nonlinear algebraic Equations (20), in which the parameters![]() ,
, ![]() and
and ![]() were computed numerically by using Simpson’s rule, has been solved numerically by using the Harwell library routine NS01A. This routine is based on a hybrid method combining the steepest descent and Newton’s methods, to obtain the numerical results presented for the first nonlinear mode of a C-C-SS-SS anisotropic rectangular plate.
were computed numerically by using Simpson’s rule, has been solved numerically by using the Harwell library routine NS01A. This routine is based on a hybrid method combining the steepest descent and Newton’s methods, to obtain the numerical results presented for the first nonlinear mode of a C-C-SS-SS anisotropic rectangular plate.
3. Applications to C-C-SS-SS Rectangular Laminated CFRP Composite Panels
Table 1, given below, shows the geometrical and material characteristics of the CFRP rectangular composite plates examined in the present work, taken from Reference [31] .
![]()
Table 1. Geometric and material properties of the rectangular plate.
In the present work, the set of admissible functions concerning C-C-SS-SS composite rectangular plates are obtained as products of linear clamped simply-supported beam mode shapes in the x- and y-directions. Such beam functions have been used previously to build plate functions and shown to be appropriate in both linear and nonlinear vibration studies [2] [5] .
The beam functions, whose analytical expressions are given in Appendix, used in the present work lead to plate-functions which satisfy all of the C-C-SS-SS theoretical boundary conditions, i.e. zero displacement along the four edges, zero slope along the two clamped edges, and zero moment with respect to x and y along the two simply supported edges.
3.1. Linear Analysis
In order to verify the accuracy of the results obtained in the present work corresponding to the C-C-SS-SS rec- tangular plate, we will compare the solution of Equation (21), that is considered as an eigen problem which will be solved by using MATLAB software, with the previous published results.
![]() (21)
(21)
The calculation was made by using 36 basic functions obtained as products of the first six clamped simply- supported beam functions, leading to square mass and rigidity matrices of dimension 25.
In Table 2, the nonlinear frequency parameters obtained from the nonlinear analysis at very small vibration amplitudes (a11 = 0.001 and 0.15) corresponding to various values of the plate aspect ratio, are compared with results obtained from linear analysis. Consequently, the results show the convergence of the nonlinear model to the linear approach at very small vibration amplitudes.
3.2. Nonlinear Analysis
Table 3 gives a summary of the first nonlinear mode shape of C-C-SS-SS rectangular plate results, corresponding to ![]() for a11 = 0.001 and 0.15, which are calculated here using 25 basic functions.
for a11 = 0.001 and 0.15, which are calculated here using 25 basic functions.
The qualitative comparison that is done in Figure 2 for the nonlinear frequency parameters of the first
![]()
Table 2. Comparison of nondimensional frequency parameters.
![]()
Figure 2. Comparison of the nonlinear frequency parameters of the first nonlinear mode of C-C-SS-SS rectangular plate. -: present work, ---: value taken from [31] corresponding to![]() .
.
![]()
Table 3. Comparison of nondimensional frequency parameters.
(a) Linear results calculated here; (b) present results obtained from nonlinear analysis for a11 = 0.001; (c) present results obtained from nonlinear analysis for a11 = 0.15.
nonlinear mode, between the results obtained here and those obtained in Reference [31] for an isotropic square plate with similar boundary conditions showed that the curve (continuous line) obtained in Bikri’s work in- creases more than the curve (dashed) corresponding to the present work. On the other hand, the comparison done with the work of B. Harras et al. in Figure 3 shows that the fully clamped anisotropic rectangular plate exhibits less nonlinearity than that examined in the present work.
In Figure 4 are plotted the nonlinear frequency versus the maximum nondimensional amplitude for the first non-linear mode shape of C-C-SS-SS rectangular plate for various values of the plate aspect ratio. All curves are similar to those mentioned in References [5] [31] .
The curves in Figure 5 and Figure 6, obtained via the present model, are plotted respectively for the values of the maximum nondimensional amplitudes![]() , and
, and
![]()
Figure 3. Comparison of the nonlinear frequency parameters of the first nonlinear mode of anisotropic C-C-SS-SS rectangular plate (present work) with anisotropic fully clamped rectangular plate (work of B. Harras et al. values taken from [5] ) corresponding to![]() .
.
![]()
Figure 4. Comparison of the change frequency of the first mode for![]() , 0.5, 0.667, and 1.5.
, 0.5, 0.667, and 1.5.
![]() , along the y-direction of the nonlinear fundamental mode shape of a rectangular plate (
, along the y-direction of the nonlinear fundamental mode shape of a rectangular plate (![]() and 0.5) corresponding to
and 0.5) corresponding to![]() . They show the amplitude dependence of the nonlinear mode shape and an increase of curvatures near to the clamped edges. On the other hand, no changes are noticed close to the simply supported ones, thereby, we suppose that the flexural stresses will increase nonlinearly near to the clamped edges accompanying increase of the vibration amplitudes.
. They show the amplitude dependence of the nonlinear mode shape and an increase of curvatures near to the clamped edges. On the other hand, no changes are noticed close to the simply supported ones, thereby, we suppose that the flexural stresses will increase nonlinearly near to the clamped edges accompanying increase of the vibration amplitudes.
Figure 7 and Figure 8 represent the nondimensional flexural stress distributions associated to the first non linear mode shape of a C-C-SS-SS rectangular plate, which show the effect of large vibration amplitudes along the x and y directions, corresponding to ![]() and
and ![]() for
for![]() . Besides, all curves show that the flexural stress is equal to zero close to the edge where the rectangular plate is simply supported, but on the other side the flexural stress exhibit a higher increase which has been proved in the linear vibration ap- proach.
. Besides, all curves show that the flexural stress is equal to zero close to the edge where the rectangular plate is simply supported, but on the other side the flexural stress exhibit a higher increase which has been proved in the linear vibration ap- proach.
4. Conclusions
The nonlinear free vibrations of C-C-SS-SS rectangular symmetrically laminated plates are studied in this paper
![]()
Figure 5. Normalized first nonlinear mode of a C-C-SS-SS rectangular plate corresponding to ![]() and
and![]() . Curve 1, lowest amplitude; Curve 3, highest amplitude.
. Curve 1, lowest amplitude; Curve 3, highest amplitude.
![]()
Figure 6. Normalized first nonlinear mode of a C-C-SS-SS rectangular plate for ![]() and
and![]() . Curve 1, lowest ampli- tude; Curve 3, highest amplitude.
. Curve 1, lowest ampli- tude; Curve 3, highest amplitude.
using a theoretical model developed previously in References [4] - [6] for geometrically nonlinear free vibrations of thin elastic structures. The objective was to determine the effects of large vibration amplitudes on the first nonlinear mode shape, the fundamental natural frequency, and the associated flexural stress distribution. The model, based on Hamilton’s principle, reduces the nonlinear free vibration problem to solution of a set of nonlinear algebraic equations involving the classical rigidity and mass tensors and a fourth order tensor due to the geometrical nonlinearity.
The study of the first nonlinear mode shape for the CFRP plates considered has shown that the curvature near the edge increases very rapidly with increase of the vibration amplitude. In addition, the mode shape close to the center of the plate becomes flatter when the amplitude increases. It was also noticed that the deformation of the mode shape, for a given value of the normalized amplitude of vibration, increases as the aspect ratio α increases. The nondimensional bending stress distribution associated with the CFRP rectangular plate first nonlinear mode shows an increase with increasing a11 which is much higher than that obtained for CFRP plates of identical aspect ratio. As a consequence of the deformation of the mode shape, a higher rate of increase was noticed in the induced bending stresses in a region close to the clamped edges. Furthermore, the nondimensional bending stress distribution associated with the CFRP rectangular plate first nonlinear mode for different amplitudes-
![]()
Figure 7. Nondimensional bending stress distribution asso- ciated with C-C-SS-SS rectangular plate first nonlinear mode along ![]() for
for![]() . Curve 1, lowest amplitude; Curve 4 highest amplitude.
. Curve 1, lowest amplitude; Curve 4 highest amplitude.
![]()
Figure 8. Nondimensional bending stress distribution associated with C-C-SS-SS rectangular plate first nonlinear mode along ![]() for
for![]() . Curve 1, lowest amplitude; Curve 4 highest amplitude.
. Curve 1, lowest amplitude; Curve 4 highest amplitude.
of vibration show a nonsymmetry along the length of the section considered because of the influence of the fiber orientation. It is worth noting here that further investigations are needed in order to check the distribution of the nonlinear bending stresses obtained at very high amplitudes of vibration.
At last, this present work enabled us to find out how the thin elastic structures behave at the large vibration amplitude by plotting different nonlinear dynamic characteristics. In addition, the qualitative comparison done with the results of an isotropic rectangular plate with similar boundary conditions obtained in reference [31] , and whith an anisotropic rectangular plate examined in reference [5] showed good and satisfactory results.
Nomenclature
![]() column matrix of total strains;
column matrix of total strains;
![]() column matrix of strains due to the in-plane displacements U, V, W;
column matrix of strains due to the in-plane displacements U, V, W;
x, y, z point co-ordinates;
![]() column matrix of bending or twisting;
column matrix of bending or twisting;
![]() column matrix of strains induced by large displacements W;
column matrix of strains induced by large displacements W;
![]() strain tensor components;
strain tensor components;
![]() stresses in the kth layer;
stresses in the kth layer;
![]() 6 × 6 matrix of transformed stiffness;
6 × 6 matrix of transformed stiffness;
![]() 6 × 6 matrix of transformed stiffness for the kth layer;
6 × 6 matrix of transformed stiffness for the kth layer;
![]() force resultant for the kth layer;
force resultant for the kth layer;
![]() moment resultant for the kth layer;
moment resultant for the kth layer;
![]() distance from the mid-plane to the layer surface of the kth layer;
distance from the mid-plane to the layer surface of the kth layer;
![]() extensional, coupling and bending stiffness coefficients for the laminated plate;
extensional, coupling and bending stiffness coefficients for the laminated plate;
![]() nondimensional extensional and bending stiffness coefficients;
nondimensional extensional and bending stiffness coefficients;
![]() matrix of coefficients corresponding to the kth harmonic;
matrix of coefficients corresponding to the kth harmonic;
![]() basic spatial functions matrix;
basic spatial functions matrix;
![]() contribution coefficient of the plate deflection function obtained as a product of the ith and jth beam mode shapes in the x and y directions respectively;
contribution coefficient of the plate deflection function obtained as a product of the ith and jth beam mode shapes in the x and y directions respectively;
a, b length, width of the plate;
E Young’s modulus;
H plate thickness;
![]() general term of the rigidity tensor, the mass tensor and the nonlinearity tensor respectively;
general term of the rigidity tensor, the mass tensor and the nonlinearity tensor respectively;
![]() general term of the nondimensional rigidity tensor, the mass tensor and the nonlinearity tensor respectively;
general term of the nondimensional rigidity tensor, the mass tensor and the nonlinearity tensor respectively;
![]() ,
,![]() in-plane displacements at point
in-plane displacements at point ![]() of the plate;
of the plate;
![]() ,
, ![]() and V bending, axial and total strain energy respectively;
and V bending, axial and total strain energy respectively;
T kinetic energy;
![]() transverse displacement at point
transverse displacement at point ![]() of the plate midplane;
of the plate midplane;
![]() nondimensional transverse displacement at point
nondimensional transverse displacement at point ![]() of the plate midplane;
of the plate midplane;
![]() maximum of the nondimensional transverse displacement;
maximum of the nondimensional transverse displacement;
![]() nondimensional parameter (plate aspect ratio) given by
nondimensional parameter (plate aspect ratio) given by![]() ;
;
![]() major Poisson’s ratio;
major Poisson’s ratio;
![]() longitudinal modulus of elasticity;
longitudinal modulus of elasticity;
![]() transverse modulus of elasticity;
transverse modulus of elasticity;
![]() shear modulus;
shear modulus;
![]() mass density per unit volume of the plate;
mass density per unit volume of the plate;
![]() ,
,![]() Frequency and nondimensional frequency parameter respectively;
Frequency and nondimensional frequency parameter respectively;
![]() ,
,![]() linear frequency and nonlinear frequency respectively;
linear frequency and nonlinear frequency respectively;
![]() dimensional bending stresses;
dimensional bending stresses;
![]() nondimensional bending stresses.
nondimensional bending stresses.
Appendix
The clamped simply-supported beam functions ![]() are defined as follows (Table 4 and Figure 9):
are defined as follows (Table 4 and Figure 9):
![]() (22)
(22)
where
![]() (23)
(23)
![]()
Table 4. The eigenvalue parameters for a C-C-SS-SS beam.
![]()
Figure 9. Clamped simply-supported beam functions for i = 1, 2, 3, 4, 5, and 6.
In which ![]() for
for ![]() are the eigen value parameters for a clamped simply-supported beam. Besides the values of the parameters
are the eigen value parameters for a clamped simply-supported beam. Besides the values of the parameters ![]() were computed solving numerically the transcendental equation
were computed solving numerically the transcendental equation ![]() by using Newton’s method.
by using Newton’s method.
![]() (24)
(24)
where
![]() (25)
(25)
G is a normalization scaling factor given by:
![]()
(26)