Moderated PEF from Transitioning between the Micro and Macroscopic Usage of Coulomb’s Law ()
1. Introduction
The dielectric effect [1] -[10] is taught in many fields including chemistry, physics, and electrical engineering. While much of the material is similar, close examination reveals differences. The textbooks are internally con- sistent, particularly when the dielectric constant is measured in circumstances similar to those where it is used.
The dielectric effect is the macroscopic manifestation of induced charge. Electrostatic interactions (and the associated dielectric effect) are foundational in all areas of chemistry including organic, physical, inorganic, biochemistry and electrochemistry. They are broadly used in molecular modeling including models for force fields, reactions, molecular structure, and ions in solution. Accompanying software is used in a wide variety of applications including the development of materials (material science), biotech, nanotech, and pharmaceuticals. Specific applications range from circuit board design to gas chromatography.
Many textbooks [6] - [9] give a dielectric version of Coulomb’s Law which incorporates the effect of induced polarization in the media.
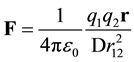 (1)
(1)
where F is the force, the dielectric constant, D, is experimentally determined, r is a unit vector pointing from q1 to q2, ε0 is the vacuum permittivity, and the electrostatic field, E, was defined as the force acting on a probe charge.
Two interpretations of Equation (1) are common in the literature. The “force between two charges” interpretation, depicted in Figure 1(a), is in ubiquitous use in molecular modeling literature. The abstract “total force acting on an individual charge” interpretation, depicted in Figure 1(b), is in Levine [10] and is consistent with textbooks on macroscopic electromagnetism [1] -[4] .
These two interpretations represent two traditions that have been used in parallel for decades. They roughly correlate with scale where researchers working with interactions within induced charge layers (computational chemistry) tend to use the interpretation of Figure 1(a). Textbooks on macroscopic electromagnetism assume the induced charge layer is infinitely thin and are consistent with the interpretation of Figure 1(b).
This paper proposes a function to transition between these two traditions. The transition function improves computational stability for many systems. Section 2 contains background material for a wide range of researchers. It also shows how the parallel traditions are consistent with distinct interpretations of the term “probe charge” used in mid-20th century textbooks. Section 3 derives the potential energy equation (PEF) for the two traditions and shows how they differ by a factor of the dielectric constant. Section 4 examines the distinguishability of the traditions. Section 5 introduces a function to transition between the traditions. Section 6 describes an analysis tool, the radial PEF, which quantifies the effect of transitioning between the traditions. Section 7 shows applica- tions in chemistry and Section 8 is the discussion.
2. Background
Coulomb’s Law [1] - [3] [11] - [13] quantifies the force between point charges in vacuum.
![]() (a) (b)
(a) (b)
Figure 1. (a) F is the total force between the two sets of charges. The dielectric constant, D, is frequently set to the permittivity, εr; (b) F is the total force acting on an individual charge, q1. The force from the induced charge surrounding q1 cancels and the force stems from the total charge due to q2 (initial and induced),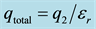 .
.
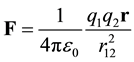 (2)
(2)
When charges are not in vacuum, the surrounding medium polarizes, forming induced charge. The macroscopic manifestation of this induced charge is the dielectric effect. It has been shown that this induced charge can be handled like any other charge ( [11] , p. 105).
2.1. A Molecular Scale Description of the Dielectric Effect
The dielectric effect is due to induced polarization including electronic polarization, field-induced rotation of molecules having permanent dipole moments, and internal rotations and vibrations that produce net dipoles, all of which oppose and reduce the imposed field. The sources of permittivity can be divided into two groups: 1) polarization stemming from rotations of dipoles, εν (i.e. due to movement of atoms), and 2) polarization stemming from electronic polarization and intra-molecular vibrations, ε∞ (primarily due to movement of electrons). Experimentally, ε∞ and εν can be distinguished, as reviewed in Gilson and Honig [14] .
In a molecular simulation, the induced charge can be determined by summing all charges within a sphere centered about the ion and averaging over time. As the radius of the sphere increases, the magnitude of the induced charge reaches a constant value, qinduced. The total charge is qtotal = q + qinduced. Electrostatic analysis of simulation results is exemplified in Warshel and Levitt [15] .
2.2. A Historical Development of Permittivity Models Based on Induced Polarization
Quantitative models relating macroscopic permittivity to microscopic polarization were developed by Debye, Onsager, Kirkwood, and Fröhlich among others. Debye developed models relating macroscopic permittivity with the polarizability of a molecule, its permanent dipole moment, and the energy of thermal agitation [16] . The model is in good agreement with experiment for gases and non-polar solvents; however it is only qualitatively correct for polar solvents.
Onsager introduced the concept of a reaction field [17] , which extended Debye’s work to polar solvents. The molecule is treated as a polarizable point dipole at the center of a spherical cavity of molecular dimensions in a continuous medium of permittivity, εr. The internal field in the cavity consists of the field that would be produced by the applied external field and the reaction field set up in the cavity by the polarization which the dipole induces in its surroundings [8] .
Debye and Onsager used macroscopic arguments for calculating the local field which limited method applicability to fluids. Kirkwood and Fröhlich used statistical methods for calculating the local field that extended method applicability. A review is provided by Hill, Vaughan, Price, and Davies [8] .
2.3. Permittivity
Relative permittivity, εr, quantizes the linear reduction in electrostatic field when charge is immersed in media. It can be experimentally measured from the change in capacitance when dielectric material is introduced [3] [10] [11] [18] - [20] and at a specific frequency the permittivity for that frequency can be determined from the refractive index [3] [20] [21] .
More formally, permittivity, ε, is the ratio of the electric flux density, D, to the electrostatic field, E. It is separated into two factors, the vacuum permittivity, ε0, which incorporates units and conventions and the relative permittivity, εr, which is unit-less.
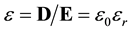 (3)
(3)
Intuitively, D is the electrostatic field due to initial charge; D has the relation to initial charge that E has to total charge. That is, just as the divergence of E is the total charge, the divergence of D is the initial charge ( [3] , p. 134).
In many cases the relation between D and E may be considered to be linear, which is the first term when D is expanded in powers of the electrostatic field. This linearity results from the normally small size of external electrostatic fields compared to internal molecular fields ( [1] , p. 36). As the electrostatic field increases, nonlinear behavior is seen ( [2] , pp. 14-16). The equations in this paper are for media that is homogeneous, isotropic, and linear.
2.4. Quantizing Induced Charge
It is often possible to determine the magnitude of induced charge. The electrostatic field stems from both initial and induced charge. When the initial charge is known, the induced charge can be back calculated. For example, for a point charge in dielectric media the electrostatic field is linearly reduced by εr. This must be equal to the field stemming from all charges, initial and induced.
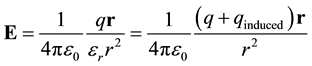 (4)
(4)
This equality shows the relation between the total charge and the initial charge ( [11] , pp. 111-113; [3] , p. 141).
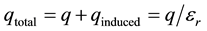 (5)
(5)
In the case of electronic polarization with permittivity of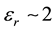 , the induced charge is half as large as the initial charge. For water with permittivity of εr = 80, the induced charge is 98.75% as large.
, the induced charge is half as large as the initial charge. For water with permittivity of εr = 80, the induced charge is 98.75% as large.
2.5. Linear Reduction of the Potential Energy Function (PEF)
The PEF is the potential energy as a function of the position of the charges. The potential energy is the integral of the negative force between charges as the charges are brought in from infinity to the position, r12. For two point charges in infinite dielectric the potential energy is given by VPEF.
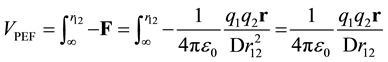 (6)
(6)
In the literature, D is frequently used to quantize the reduction of potential energy. The dielectric media is assumed to be infinite, the charges are point charges that are fully formed at infinity, these charges are surrounded by induced charge at all positions (including infinity), and the zero point energy is defined as the state where the point charges are an infinite distance apart from each other.
In practice, D is set to a constant or a function (e.g. Gelin and Karplus [22] ). Empirical and simulation techniques are employed to ascertain the best value or function for D where the long distance term is set to the macroscopic result. In electrostatic literature, there are three distinct definitions of D as the dielectric constant, as electric flux density, and as a function denoting the reduction of potential energy.
2.6. The Work Equation and the PEF
On the face of it, the work equation has the same permittivity dependence as the PEF. However, examination of the derivation of the work equation shows that a bare charge is brought in from infinity. In the PEF, all charges are surrounded by induced charge at all positions. The permittivity dependence of the work equation and the PEF are not the same.
2.7. A Probe Charge and Two Interpretations of Coulomb’s Law
Many textbooks use the dielectric version of Coulomb’s Law, Equation (1), where the electrostatic field is defined as the force acting on a probe charge, see Smythe ( [6] , pp. 2-5), Davies ( [8] , pp. 7-8), Alberty & Silbey ( [9] , p. 237), and Newman & Thomas-Alyea ( [7] , pp. 85-87). Fried [23] and Atkins [20] teach Equation (1) with- out mention of a probe charge.
Two interpretations of the dielectric Coulomb’s Law are depicted in Figure 1. Figure 1(a) shows the force between charges where the dielectric constant, D, is determined empirically. Some textbooks (e.g. Fried, [23] , p. 836) set this empirical constant to the permittivity, D = εr. Figure 1(b) shows the total force acting on an individual charge as seen in Levine ([10] , pp. 433-434).
Since Equation (1) holds for a probe charge, the definition of “probe charge” reflects on the intended interpretation of Equation (1). The probe charge can be interpreted either as a small charge with surrounding induced charge, or as an individual charge exclusive of induced charge. That is, while one of the charges in Equation (1) has surrounding induced charge, the other charge does or does not, depending on the interpretation of “probe charge”. Two definitions for “probe charge” are depicted in Figure 2.
Smythe defines a probe charge to be a charge so minute that no redistribution of charge takes place due to its
![]() (a) (b)
(a) (b)
Figure 2. The electrostatic field is the force acting on a probe charge. A probe charge can be defined as (a) a small charge with induced charge or (b) a hypothetical charge independent of induced charge.
presence ( [6] , pp. 2-5). It is not clear if the charge simply does not perturb the field due to the other charges, or if, in addition, the charge does not induce a charge about itself.
Classically, a charge always induces charge about itself, regardless of size: The magnitude of induced charge is proportional to the magnitude of the initial charge. As the initial charge becomes smaller, the induced charge becomes proportionally smaller. This interpretation of “small charge” maps onto Figure 1(a) and Fig- ure 2(a).
Alternately, one can imagine an abstract, hypothetical charge that does not induce charge about itself. This hypothetical charge interpretation is consistent with Figure 1(b) and Figure 2(b).
These different interpretations of the probe charge are consistent with the different usages of Equation (1) that are seen in the literature. The “small charge with surrounding induced charge” definition is consistent with a “total force between two charges” interpretation. The “small charge without surrounding induced charge” is consistent with the “total force acting on an individual charge” interpretation.
Probe charges are no longer used in textbooks on electromagnetism [1] -[5] removing this ambiguity. Several chapters are used to develop electrostatic theory ([1] , pp. 34-85; [2] , pp. 2-173; [3] , pp. 33-163; [4] ) where approximations, assumptions, and definitions are used to develop a robust description of macroscopic electrostatic theory. This theory is consistent with the “total force acting on an individual charge” interpretation of Equation (1) and the interpretation depicted in Figure 1(b), Figure 2(b), and Figure 3(b).
At the molecular scale, some of the approximations and assumptions used in macroscopic analysis do not hold. In particular, at the macroscopic scale the induced charge layer is assumed to be infinitely thin, whereas in chemistry much of the data is based on interactions within the induced charge layer of multiple charges.
3. The PEF for the Two Traditions
In the derivation of the PEF, the force is the total force between charges. The two traditions use different equations for this force as depicted in Figure 3.
In Figure 3(a), the total force between charges q1 and q2 is given by Equation (1). In molecular modeling, D is generally set to εr, D = εr.
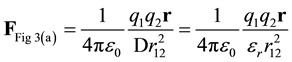 (7)
(7)
The potential energy, VFig 3(a), is found by integration.
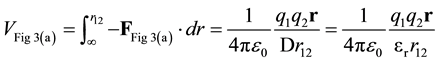 (8)
(8)
In Figure 3(b), the total force between q1 and q2 is determined by substituting the total charge (initial and induced) into Coulomb’s Law, i.e. substitute total charge from Equation (5) in for both charges in Equation (2).
![]() (a) (b)
(a) (b)
Figure 3. (a) Force is reduced by a factor of D, frequently D is set to the permittivity, D = εr; (b) The total charge for a point charge (initial and induced) is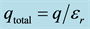 . Substituting into Coulomb’s Law results in permittivity squared in the denominator.
. Substituting into Coulomb’s Law results in permittivity squared in the denominator.
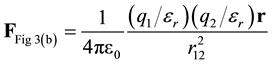 (9)
(9)
Again, the potential energy is found by integration.
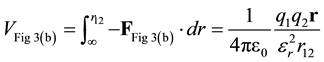 (10)
(10)
The two traditions in Figure 3 result in potential energies, Equations (8) and (10), which differ by a factor of εr.
4. Distinguishability of Traditions
When permittivity is large, the two traditions are empirically similar. For example, in water the permittivity is about 80, ![]() , and the potential energy is linearly reduced by D = 80 or D = 6400 (Equations (8) and (10) respectively, D taken from Equation (6)). Experimentally, the reciprocals of 80 and 6400 are both small and only a sensitive measurement would distinguish them.
, and the potential energy is linearly reduced by D = 80 or D = 6400 (Equations (8) and (10) respectively, D taken from Equation (6)). Experimentally, the reciprocals of 80 and 6400 are both small and only a sensitive measurement would distinguish them.
The two traditions can be distinguished in cases where εr is small resulting in terms that are sufficiently large to be measured. That is, for electronic polarization where εr = ~2, the PEFs are reduced by a factor of 2 and 4 (Equations (8) and (10) respectively) and this difference can be experimentally measured.
The traditions can also be distinguished in cases where, even though εr is large, there are a large number of interactions and the sum of the interactions is measureable as discussed below in the section on the radial PEF.
When the dielectric constant is measured in circumstances similar to those where it is used, then the two traditions are similar. For example, Figure 4 shows a model for an effective dielectric which transitions between the two traditions. For an application with charges at distance, r, measuring the dielectric constant at that distance results in a value that is correct for that distance. That is, use of Coulomb’s Law as interpreted in Figure 1(a) enables the use of a distance-appropriate dielectric constant for interactions inside the induced charge layer.
5. Incorporating the Classical Result into the PEF with an Effective Dielectric, Deff
When polarization is approximated to be pairwise separable, a pairwise function can be used to describe the dielectric effect. Then force field models can incorporate classical electrostatic theory with an effective dielectric, Deff.
Deff is the effective dielectric constant at distance, r (See Figure 4). At short distances where there is little induced charge, the effective dielectric is close to unity. As distance increases, induced charge inside that distance
![]()
Figure 4. An effective dielectric function rationalizes the two traditions. Inside the induced charge layer, the dielectric effect is reduced. As distance increases, the effective dielectric increases until it reaches the macroscopic value of![]() .
.
increases and the effective dielectric increases as the induced charge layer is traversed. At distances outside the induced charge layer, the macroscopic value is used,![]() . At very short distances, local features dominate and the effective dielectric approximation may not be accurate. This transition function assumes the dielectric effect is pairwise separable and it is an extension of pairwise functions used in the literature (e.g. Lazaridis [24] and Zoebisch [25] ).
. At very short distances, local features dominate and the effective dielectric approximation may not be accurate. This transition function assumes the dielectric effect is pairwise separable and it is an extension of pairwise functions used in the literature (e.g. Lazaridis [24] and Zoebisch [25] ).
Many molecular simulations have terms spanning the range between molecular and classical distances. The effective dielectric handles interactions at all distances and enables the utilization of both traditions. For example a simulation of substrate in condensed phase typically has media that extends to infinity. In this simulation some terms are for interactions within induced charge layers and others are for interactions beyond the induced charge layer.
The question remains, under what circumstances is it important to transition between the traditions?
6. The Radial PEF Function; Evaluating the Effect of Transitioning between the Traditions
The magnitude of the potential energy between two charges decreases with distance and long distance terms are very small. However, the number of terms at this distance is large. Is the number of terms large enough for long distance terms to be important? The radial PEF quantifies the net effect of these terms. The radial PEF is related to the radial distribution function. It is independent of approximation and can be applied to an exact wavefunc- tion as well as to a trajectory from a force field model.
For a charge, q, and a distance, r, the radial PEF at r is the sum of potential energy terms for all charges at distance r from q. The integrated radial PEF is the sum over r of the radial PEFs. Examination of the PEF shows that it is equal to the sum of all integrated radial PEF’s divided by 2 since every interaction is counted twice.
In the radial PEF, the magnitude of each charge-charge interaction decreases linearly with inverse distance, but the number of interactions increases by r2, i.e. for a constant density of charges, the number of charges at distance, r, increases in proportion to the surface area of a sphere of radius r centered at q, 4πr2. As a result, the radial PEF increases linearly with distance. The sum over all distances is the integral over r resulting in an inte- grated radial PEF that depends on r2. Ostensibly this means that the PEF also depends on r2 and extending to in- finity produces an infinite PEF.
For a neutral system, there are equal numbers of positive and negative charges. In most chemical systems, counter-ions are associated with each other and the terms in a region approximately cancel. That is, for large dis- tances the PEF is the sum of a very large number of positive and negative numbers which can affect computa- tional stability. Algorithmic methods can be used to improve computational stability.
Any charge distribution can be represented as an infinite series consisting of the net charge, a dipole, a qua- drapole, and higher order multipoles ( [11] , p. 66). For determining the radial PEF, interactions with charges at a distant region can be approximated as interaction with this infinite series, creating terms for the net charge, the dipole, and higher order multi-poles.
The net charge in a region depends on the characteristics of the system; while it tends toward zero, there may be a net charge in a region (e.g. in a dilute salt solution). The dipole moment is significant within the induced charge layer; indeed the induced charge layer frequently consists of induced dipoles. Outside the induced charge layer, dipole moments return to bulk structure.
The potential energy between two charges varies as ![]() as noted above. The potential energy between a charge and a dipole varies as
as noted above. The potential energy between a charge and a dipole varies as![]() , and the quadrapole term varies as
, and the quadrapole term varies as![]() . In the radial PEF, these are multip- lied by the number of charges at distance, r. Then the charge portion of the radial PEF is linear with distance as discussed above. The dipole radial PEF is independent of distance and the quadrapole radial PEF varies with
. In the radial PEF, these are multip- lied by the number of charges at distance, r. Then the charge portion of the radial PEF is linear with distance as discussed above. The dipole radial PEF is independent of distance and the quadrapole radial PEF varies with![]() . Higher order terms decrease faster than
. Higher order terms decrease faster than ![]() and drop out.
and drop out.
Deff can be modeled as linear with distance. When this Deff is incorporated into the radial PEF, it reduces distance dependence by a factor of r for interactions within the induced charge layer. Then the charge term is independent of distance and the dipole term varies as![]() . The average value of the dipole moment at distance r may decrease with distance, with further reduction in distance dependence. The quadrapole term varies as
. The average value of the dipole moment at distance r may decrease with distance, with further reduction in distance dependence. The quadrapole term varies as ![]() and drops out for large r. Outside the induced charge layer, Deff levels out to the macroscopic value further mod- erating the PEF as compared with the PEF produced using the tradition of Figure 1(a).
and drops out for large r. Outside the induced charge layer, Deff levels out to the macroscopic value further mod- erating the PEF as compared with the PEF produced using the tradition of Figure 1(a).
7. Applications in Chemistry
When the induced charge layer is thin, then the transfer between traditions occurs within a short distance. An example is electronic polarization. Outside the induced charge layer, macroscopic equations hold and![]() . At van der Waals distances, the force field models are parameterized for D = 1. The dielectric effect transitions between D = 1 and D = 4. For the carboxylic acid dimer, when a force field is parameterized to produce a bonding energy of 6 kcal/mole for D = 1, then when the acids are separated by media the electronic polarization of the media becomes important and can be incorporated by setting D = 4. If the D = 4 result is used when the acids are directly bonded, then the carboxylic acid dimer will be calculated to have a 1.5 kcal/mole bonding energy in- stead of the intended 6 kcal/mole.
. At van der Waals distances, the force field models are parameterized for D = 1. The dielectric effect transitions between D = 1 and D = 4. For the carboxylic acid dimer, when a force field is parameterized to produce a bonding energy of 6 kcal/mole for D = 1, then when the acids are separated by media the electronic polarization of the media becomes important and can be incorporated by setting D = 4. If the D = 4 result is used when the acids are directly bonded, then the carboxylic acid dimer will be calculated to have a 1.5 kcal/mole bonding energy in- stead of the intended 6 kcal/mole.
When the induced charge layer is thick, the number of electrostatic interactions at a given distance becomes important as seen in Table 1 showing the distance dependence of the radial PEF.
The charge term is significant when the sum of charges in a region is not zero (for example, when charges are not closely associated with their counter charges as seen in dilute salt solutions).
The dipole term is a significant portion of the radial PEF for many calculations. As distance increases, dipole moments continue to contribute to the induced charge until the edge of the induced charge layer is reached and the dipoles return to bulk structure. The distance dependence of the dipole radial PEF is![]() , producing an integrated radial PEF of ln(r). This result depends strongly on the average dipole moment as a function of distance. In cases where the average dipole moment decreases with distance, the distance dependence will also decrease. Even where the distance dependence is strongly attenuated, the decrease continues until Deff reaches the macroscopic value.
, producing an integrated radial PEF of ln(r). This result depends strongly on the average dipole moment as a function of distance. In cases where the average dipole moment decreases with distance, the distance dependence will also decrease. Even where the distance dependence is strongly attenuated, the decrease continues until Deff reaches the macroscopic value.
The quadrapole radial PEF will tend to drop out for large distances due to the ![]() dependency.
dependency.
8. Discussion
Examination of Coulomb’s Law as it is used in different fields elucidates the dielectric effect in different cir- cumstances. This material can be used to inform the parameterization of force field models, solvent models, and matrix models where distances range from molecular scales to macroscopic scales.
![]()
Table 1. The radial PEF can be written as the sum of net charge terms, dipole terms, and quadrapole terms. The net charge in a region is small or zero for many systems. The quadrapole term drops out for large distances leaving a sum of dipole terms. There is further reduction in distance dependence when the average dipole moment decreases with distance.
The dielectric effect is a linear response and different fields of research focus on the linear reduction of different quantities. The dielectric constant can represent a linear reduction of force between charges, consistent with Figures 1(a)-3(a). The dielectric constant can also represent a linear reduction of electrostatic field consistent with Figures 1(b)-3(b).
For the purposes of this Discussion, D quantifies the linear reduction of the potential energy as seen in Equation (6). Setting D = εr results in Equation (8) and setting ![]() results in Equation (10). Ostensibly, the two traditions result in equations for the PEF that differ by a factor of εr. The traditions have been used in parallel for decades and are self-consistent.
results in Equation (10). Ostensibly, the two traditions result in equations for the PEF that differ by a factor of εr. The traditions have been used in parallel for decades and are self-consistent.
Equation (8) (D = εr) has been in ubiquitous use in computational chemistry literature for over 20 years. It is used in force field model software for pharmaceuticals, biotech, nanotech, and materials (material science). For example, a web search finds over 12 million cached pages that cite software (AMBER or CHARMM) where users set D = εr.
Equation (10) (![]() ) was derived using classical electrostatic theory where the induced charge layer is assumed to be infinitely thin. This result is the substitution of a textbook equation for total charge into the textbook equation for the PEF. Consistent with this result; industry researchers frequently state during their talks at national ACS meetings that D = 4 produces better correlation with experiment than D = 2 for electronic polarization where
) was derived using classical electrostatic theory where the induced charge layer is assumed to be infinitely thin. This result is the substitution of a textbook equation for total charge into the textbook equation for the PEF. Consistent with this result; industry researchers frequently state during their talks at national ACS meetings that D = 4 produces better correlation with experiment than D = 2 for electronic polarization where ![]() and where the induced charge layer is thin.
and where the induced charge layer is thin.
Smythe’s classic textbook on electromagnetism [6] (with editions spanning 1936-1967) uses the dielectric version of Coulomb’s Law, Equation (1). Smythe is consistent with both traditions, depending on the interpretation of “probe charge”. Interestingly, the probe charge is mentioned two pages after Coulomb’s Law is given. It seems contrived to state that the use of the probe charge implies that one of the charges in Coulomb’s Law is a hypothetical charge without surrounding induced charge. It is a focus in this paper since it corresponds closely with contemporary textbooks on electromagnetic theory [1] - [4] .
Examination of multiple textbooks from several fields reveals that both traditions are currently in use, possibly stemming from different interpretations of Smythe and his contemporaries. The two traditions roughly correlate with scale where researchers working with interactions within induced charge layers tend to use the interpretation of Figures 1(a)-3(a). Textbooks on macroscopic electromagnetic theory assume the induced charge layer is infinitely thin and are consistent with the interpretation of Figures 1(b)-3(b).
The two traditions may have developed due to different experiences of the magnitude of electrostatic interactions. That is, experience with interactions within the induced charge layer verses experience with interactions outside the induced charge layer. Complexity is compounded if the induced charge layer is thicker than thought: in water a linear Deff and the macroscopic result that D = 6400 would result in an induced charge layer that is thousands of angstroms wide.
The two traditions can be rationalized with a distance dependent function as depicted in Figure 4. At distances inside the induced charge layer, an effective dielectric, Deff, is measured at that distance. Deff increases as distance increases and the induced charge layer is traversed. As distance reaches the edge of the induced charge layer, Deff reaches the classical theoretical result,![]() . The shape of the Deff function will vary with substrate and matrix.
. The shape of the Deff function will vary with substrate and matrix.
In PEF calculations, Deff increases the magnitude of local terms as compared to cumulative long distance terms. For example, in water the cumulative long distance PEF is decreased by a factor of 80, reducing the impact of mid and long distance terms on convergence and local effects.
Use of the interpretation in Figure 1(a) is very versatile; regardless of position within (or outside) the induced charge layer, measuring the dielectric constant in similar conditions produces the correct result. For macroscopic analysis, the interpretation in Figure 1(b) enables the use of electrostatic theory and large databases of permittivities based on capacitance data. The theoretical result can be used when the term is too small to directly meas- ure. When polarization can be approximated by a pairwise function, classical electrostatic theory can be incor- porated into PEFs by use of an effective dielectric function Deff. Use of Deff is important wherever cumulative long distance terms are significant.
Acknowledgements
Special appreciation is extended to Dr. Dana Backman for editorial comment.