1. Introduction
“Symmetry, as wide or narrow as you may define its meaning, is one idea by which man through the ages has tried to comprehend and create order, beauty, and perfection.”—Hermann Klaus Hugo Weyl (1885-1955)
Just shortly after Professor Albert Einstein (1897-1955) announced his General Theory of Relativity (GTR) in a series of lectures delivered before Germany’s Prusian Academy of Science culminating on November 25, 1915; the great German mathematician, mathematical physicist and philosopher—Professor Herman Weyl (1885-1955) began an intensive study of the GTR’s mathematical structure and began publishing related scientific papers dealing with its physical applications.
In 1918, Professor Weyl published his book Raum Zeit Materie (Space-Time-Matter), a book which beautifully exemplifies the fruitful, harmonious and the natural interplay between mathematics, physics and philosophy—amongst others, this book provided the first fully comprehensive analysis of the geometric aspects of Professor Einstein’s GTR and its relationship with spacetime and physics. In this book—Raum Zeit Materie, Professor Weyl set himself the task to provide a deep and profound mathematical and philosophical elucidation of the problem of space and time in general terms. Because gravitation and electromagnetism where the only forces known to humankind at the time, it was natural for Professor Weyl and others (including Professor Einstein), to assume that this task of finding a UFT would only involve the unification of gravity and electromagnetism.
One of the topics covered—perhaps the most outstanding topics covered in the book—Raum Zeit Materie, is Professor Weyl’s great but failed idea that gravity and electromagnetism might both be derivable from a generalization of Riemann geometry i.e., from the same mathematical basis from which Professor Einstein had developed his relativity theory. Professor Weyl’s great idea was based on a new mathematical symmetry that he called gauge invariance. This theory gave birth to the modern concept of the gauge principle; a principle without which any of the modern efforts to finding an all-encompassing unified field theory could not be. It underlies and underpins all of the Yang-Mills theories and is a sacrosanct cornerstone in string and string-related theories, especially string theory’s more recent variant, M-theory.
Professor Weyl’s theory was given a still birth by its most able midwife—Professor Einstein. Professor Einstein greatly admired the theory but with equal passion, he would not make it take its “first gulp of air” nor have just “one photon fall on the retina” of the newly born theory. Professor Einstein’s razor sharp and agile intellect saw the “tiny little devil in the detail of the beauty of Professor Weyl’s theory” and immediately thereafter, he delivered his all-enduring and lethal blow to it, a blow that made sure it would never raise.
Lo and behold! What resurrected from Professor Weyl’s theory is the “ghost” of gauge invariance, this is about all that remained of its beauty after the crumbling of its entire edifice. Today, this “ghost” (of gauge invariance) pervades all of physics that makes the endeavour on which Professor Weyl was failed by Einstein i.e., it pervades and permeates all unification efforts. For example, in virtually all modern quantum gauge theories, Professor Weyl’s gauge concept is used to justify the “mathematical chicanery and shenanigan” called renormalization! Renormalization is when one subtracts an artificial infinity from a calculated infinity to get a usable or useful, finite answer. Without this, most if not all modern unification efforts would have their entire edifice come down crumbling like as happened with Professor Weyl’s theory at the able hands of Professor Einstein.
In this reading, we stand right outside the tomb of Professor Weyl’s theory and call forth his theory—“arise” we say! We demonstrate that Professor Einstein’s criticism is easily overcome without much difficultly. We recast Professor Weyl’s theory by resetting its foundation stone in which process we completely overcome Professor Einstein’s lethal and venomous criticism. Having overcome Professor Einstein’s criticism—a fresh new life is thereby breathed into the nostrils of Professor Weyl’s theory; we see nothing hindering its further developed as a physical theory from here-on since its greatest obstacle is now afield and afar, somewhere in the peripheries of the distant roadside. As a way of demonstrating what we have in mind insofar as the further development of Professor Weyl’s theory, we lie down in §(7.2) the main ideas of a unified theory that we are currently working on.
For instructive purposes, in §(2) and (3) we give an exposition of the concept of invariance of length in Riemann and Weyl geometry. In §(4), we give an animated criticism of Professor Einstein’s to Professor Weyl’s unified theory. In §(5), having given an exposition of Professor Weyl’s theory and the criticism level against it, we proceed to recast this theory in a form that overcomes Professor Einstein’s otherwise lethal criticism. In §(6), fruits of recasting Professor Weyl’s theory are reaped and finally in §(7), a general discussion is given and the conclusion drawn thereof lied down.
2. Length Invariance in Riemann Geometry
First and foremost, one will recall from elementary geometry that the square of the magnitude or length 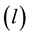 of a vector
of a vector 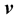 is defined by the dot product
is defined by the dot product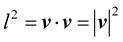 . In tensor notation and in particular—in Riemann geometry, for an arbitrary vector
. In tensor notation and in particular—in Riemann geometry, for an arbitrary vector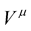 , we write this as:
, we write this as:
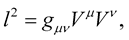 (1)
(1)
where as usual 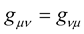 is the symmetric metric tensor of spacetime. Now, taking the total derivative of this expression, we will have:
is the symmetric metric tensor of spacetime. Now, taking the total derivative of this expression, we will have:
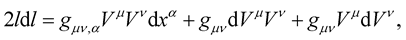 (2)
(2)
and using the identity or fact that 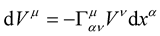 see e.g., [1] -[3] [or any good book of general relativity ] where
see e.g., [1] -[3] [or any good book of general relativity ] where 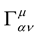 is the usual three Christophel symbol of Riemann geometry, the above reduces to:
is the usual three Christophel symbol of Riemann geometry, the above reduces to:
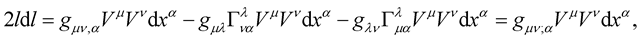 (3)
(3)
that is:
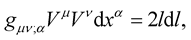 (4)
(4)
where:
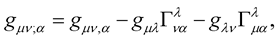 (5)
(5)
is the usual covariant derivative of the metric tensor in Riemann geometry. In Riemann geometry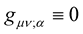 , the meaning of which is that
, the meaning of which is that 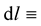 0, simple stated, the length of a vector is invariant under translation of the frame of reference or the coordinate system. Clearly, the covariant derivative
0, simple stated, the length of a vector is invariant under translation of the frame of reference or the coordinate system. Clearly, the covariant derivative 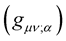 determines whether or not the length of a vector is invariant or not—it determines the resulting nature and property of the space under consideration. The condition
determines whether or not the length of a vector is invariant or not—it determines the resulting nature and property of the space under consideration. The condition 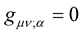 is the foundation stone of Riemann geometry as this condition defines the structure and nature of Riemann geometry. Actually—as will be demonstrated latter; through the assumed symmetries of the metric and the affine (i.e.,
is the foundation stone of Riemann geometry as this condition defines the structure and nature of Riemann geometry. Actually—as will be demonstrated latter; through the assumed symmetries of the metric and the affine (i.e., 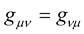 and
and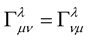 ) the condition
) the condition 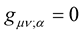 allows us to define the affine
allows us to define the affine 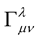 as a function of the metric tensor
as a function of the metric tensor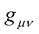 .
.
At this point, Professor Weyl must have wondered if Riemann geometry could be altered in such a way that 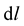 does not vanish as it does in ordinary Riemann geometry. While thinking about this, a mental visitation in the form of a thought must have occurred to Professor Weyl, a thought to the effect that, if the metric is re-gauged or transformed from
does not vanish as it does in ordinary Riemann geometry. While thinking about this, a mental visitation in the form of a thought must have occurred to Professor Weyl, a thought to the effect that, if the metric is re-gauged or transformed from 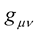 to
to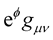 , i.e.:
, i.e.:
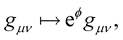 (6)
(6)
where 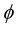 is a scaler; he would achieve his desire of a none vanishing
is a scaler; he would achieve his desire of a none vanishing 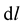 because if
because if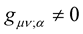 , it follows from (4) that
, it follows from (4) that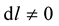 . As we will demonstrate latter on in this reading, if he [Professor Weyl] really wanted to do away with Riemann geometry, he must have not compromised and tried to remain within its confines and domains.
. As we will demonstrate latter on in this reading, if he [Professor Weyl] really wanted to do away with Riemann geometry, he must have not compromised and tried to remain within its confines and domains.
As to what might have motivated Professor Weyl into thinking of varying the length of the vectors may very well be the fact the in Riemann geometry while lengths of vectors are preserved, their directions in space are not, so Professor Weyl might have wondered: if the directions are not preserved, why should the lengths be preserved?! With this noble thought, Professor Weyl must then have embarked onto his intellectual journey of the mind of attaining a non-Riemann geometry with non-preserved lengths of vectors which would bring about what Dr. Alexander Afriat [1] calls mathematical justice—i.e., if the angle is not invariant upon parallel transport, why should the length remain invariant? Does not justice demand that if the angle is not invariant, so should the length since these are the only important attributes of a vector.
3. Length Variation in Weyl Geometry
As a starting point, in lieing down the foundation stone of his theory, having glimpsed into the marvellous structure and nature of Riemann geometry as lied-down above, Professor Weyl had two things in mind, first of which was the idea of a none vanishing covariant derivative i.e. 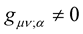 and second, the idea of a none vanishing length of vectors i.e.
and second, the idea of a none vanishing length of vectors i.e.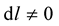 . To achieve the former, Professor Weyl inspected the identity or fact that
. To achieve the former, Professor Weyl inspected the identity or fact that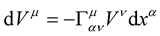 . This identity gives the change of length of a vector
. This identity gives the change of length of a vector 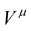 under any given transformation or translation. Providentially, Professor Weyl assumed that a change in the vector magnitude dl, must obey a similar expression. By the adroitness of the mind, Professor Wely proceeded to make his analogue, which is:
under any given transformation or translation. Providentially, Professor Weyl assumed that a change in the vector magnitude dl, must obey a similar expression. By the adroitness of the mind, Professor Wely proceeded to make his analogue, which is:
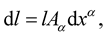 (7)
(7)
where 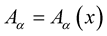 is a hitherto mysterious four vector quantity of unknown origins, its duty, sole purpose and ultimate mission is simple to keep
is a hitherto mysterious four vector quantity of unknown origins, its duty, sole purpose and ultimate mission is simple to keep 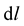 from vanishing—for as long as
from vanishing—for as long as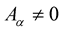 , we will have
, we will have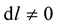 . The relationship (7), Professor Weyl was to embellish by holding it sacrosanct as the foundation stone of this new theory; regrettably, it is a relationship which he would defend right up to his untimely and unexpected passing-over in 1955. He died1 in Zürich—Switzerland, suddenly, of a heart attack, on December 9, 1955.
. The relationship (7), Professor Weyl was to embellish by holding it sacrosanct as the foundation stone of this new theory; regrettably, it is a relationship which he would defend right up to his untimely and unexpected passing-over in 1955. He died1 in Zürich—Switzerland, suddenly, of a heart attack, on December 9, 1955.
Now, having set the battle-lines through (7), Professor Weyl proceeded by the sleight of hand to insert this relationship into (4) thus obtaining:
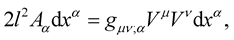 (8)
(8)
which reduces to:
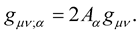 (9)
(9)
The relationship (9) justifies (7).
Now, we have to calculate the resulting affine connections from the new covariant derivative (9). For this, we will have to write down the three expressions that result from a cyclic permutation of the indices 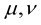 and
and 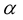 in
in 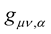 and
and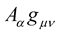 , that is:
, that is:
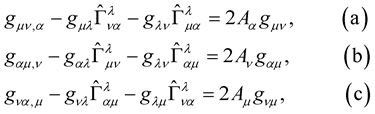 (10)
(10)
where the hat on 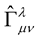 has been put so that it is made clear that this affine is no longer the same Christoffel symbol as the one used in Riemann geometry.
has been put so that it is made clear that this affine is no longer the same Christoffel symbol as the one used in Riemann geometry.
Now, subtracting Equation (10a) from the sum of (10b) and (10c) and by making use of the symmetries 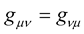 and
and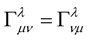 , one obtains:
, one obtains:
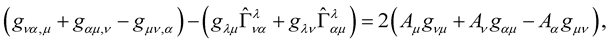 (11)
(11)
and by raising the index 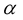 and making
and making 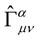 the subject of the formula, one obtains:
the subject of the formula, one obtains:
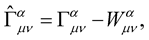 (12)
(12)
where:
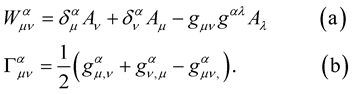 (13)
(13)
The new object 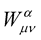 is the Weyl tensor while
is the Weyl tensor while 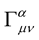 is the usual Christoffel three symbol. The geometry that we have just described with the affine connection
is the usual Christoffel three symbol. The geometry that we have just described with the affine connection 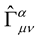 is what is called Weyl geometry. This geometry tends to Riemann geometry as
is what is called Weyl geometry. This geometry tends to Riemann geometry as 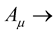 0. What deeply intrigued Professor Weyl and many others that came to admire the new theory is the fact that the Weyl connection
0. What deeply intrigued Professor Weyl and many others that came to admire the new theory is the fact that the Weyl connection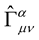 , is invariant under the following transformations:
, is invariant under the following transformations:
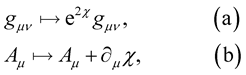 (14)
(14)
where 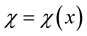 is an arbitrary scaler function. If
is an arbitrary scaler function. If 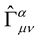 is invariant under the transformation (14) i.e.
is invariant under the transformation (14) i.e.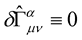 , the curvature tensor
, the curvature tensor 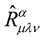 is also invariant i.e.
is also invariant i.e.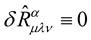 . Given that Professor Weyl knew very well that Maxwellian electrodynamics is described by a four vector such that the entire Maxwellian electrodynamics is invariant under the transformation (14b), without wasting much time, Professor Weyl seized the golden moment and identified
. Given that Professor Weyl knew very well that Maxwellian electrodynamics is described by a four vector such that the entire Maxwellian electrodynamics is invariant under the transformation (14b), without wasting much time, Professor Weyl seized the golden moment and identified 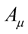 with the Maxwellian four vector potential of electrodynamics. At this point, one can not help but endlessly and deeply admire Professor Weyl’s brilliantly convinced theory, and on the other hand, one can only be irretrievably and deeply sad to know that this theory, despite its esoteric grandeur and exquisite beauty, it does not correspond with experience.
with the Maxwellian four vector potential of electrodynamics. At this point, one can not help but endlessly and deeply admire Professor Weyl’s brilliantly convinced theory, and on the other hand, one can only be irretrievably and deeply sad to know that this theory, despite its esoteric grandeur and exquisite beauty, it does not correspond with experience.
4. Einstein’s Criticism
Professor Weyl’s proposed theory led to a rescaling of the fundamental metric tensor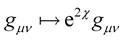 . He [Professor Weyl] held that, this rescaling should have no effect on physics. As aforestated, Professor Einstein initially loved the idea—alas, the devil was in the detail; he noted that the line element
. He [Professor Weyl] held that, this rescaling should have no effect on physics. As aforestated, Professor Einstein initially loved the idea—alas, the devil was in the detail; he noted that the line element 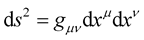 would also be rescaled according to
would also be rescaled according to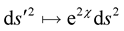 . Since
. Since 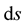 can be made to serve as a measuring rod or clock, the agile Professor Einstein was quick to note that this would mean that certain absolute quantities, such as the spacing of atomic spectral lines and the Compton wavelength of an Electron for example, would change arbitrarily and thus have to depend on their prehistory. With this, Professor Einstein delivered the lethal and venomous blow to Professor Weyl’s theory and concluded that it must therefore be non-physical—despite its grandeur and beauty, it had no correspondence nor bearing with physical and natural reality.
can be made to serve as a measuring rod or clock, the agile Professor Einstein was quick to note that this would mean that certain absolute quantities, such as the spacing of atomic spectral lines and the Compton wavelength of an Electron for example, would change arbitrarily and thus have to depend on their prehistory. With this, Professor Einstein delivered the lethal and venomous blow to Professor Weyl’s theory and concluded that it must therefore be non-physical—despite its grandeur and beauty, it had no correspondence nor bearing with physical and natural reality.
Thus, from a “safe distance”, the great Professor Einstein was the first to publicly exhibit his passionate albeit backhanded admiration of Professor Weyl’s theory, he said of it2
“…apart from the agreement with reality, it is at any rate a grandiose achievement of the mind… a first class [stroke of] genius.”
With equal passion, he made the one all-enduring “aerial bombardment” to it, a bombardment from which Professor Weyl’s theory would never recover to this day.
Stated in a different manner, the agile Professor Einstein was quick and to point out that in Professor Weyl’s geometry, the frequency of the spectral lines of atomic clocks from different portions of the distant heavenly spaces would depend on the location and pre-histories of the atoms. This is in fragment disagreement with experience. The spectral lines are well-defined and sharp; they appear to be independent of an atom’s pre-history. Atomic clocks define units of time, and experience shows they are integrally transported from one portion of the heavens to the other. So, with this criticism alone, Professor Einstein gave Professor Weyl’s theory a stillbirth with his backhanded compliant.
Professor Weyl’s brilliant and beautiful theory was hopelessly thwarted and, to no avail, he made last ditch efforts to save his theory some years after his first publication [5][6] . Professor Einstein’s criticism lie deep in the nimbus of the foundation stone of Professor Weyl’s theory, which is that the length of a vector varied from one point of spacetime to another. In wrapping-up his criticism, he [Einstein] said of it3:
“... I do not believe that [this] theory will hold its ground in relation to reality.”
Much for the great Professor Hermann Weyl and his all-brilliant, beautiful but supposedly “failed” theory. Can it [the theory] be saved? As already stated, Professor Weyl himself made attempts [5] [6] and, he was not alone in this as pre-eminent and notable figures such as Sir Professor Arthur S. Eddington [8] and the great Professor Paul A. M. Dirac [9]come aboard to help in defending the theory. All attempts so far at trying to save the theory have not gained much attention or universal recognition and appeal simple because these attempts are stuck in Professor Weyl’s quagmire and conundrum of holding sacrosanct the Weyl hypothesis (7).
Shortly, we will demonstrate that indeed Professor Weyl’s theory can be saved first by dropping (7) and reverting back to the humble Riemann condition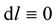 . In our recasting of Professor Weyl’s theory, we are to hold sacrosanct the Weyl gauge transformation (14) and not the Weyl hypothesis (7).
. In our recasting of Professor Weyl’s theory, we are to hold sacrosanct the Weyl gauge transformation (14) and not the Weyl hypothesis (7).
5. Recasting of Weyl’s Theory
In recasting Professor Weyl’s theory so that it overcomes once and for altime Professor Einstein’s criticism, we will not take the traditional route that was taken by Professor Weyl because in so doing, we will fall into the same trap which the great Professor Weyl fell victim to. At our point of departure, we wave goodbye to Riemann geometry and efferently prepare to embrace a totally new geometry, a hybrid Riemann geometry which has the same features as the Weyl geometry—less off-cause, the change of length of vectors under transformations or translations. The route that we are about to take is equivalent and the reason for changing the sails is that the present route allows us to demonstrate latter how Professor Weyl would have overcome Professor Einstein’s criticism. Actually, this route allows us to pin-down exactly where Professor Weyl’s theory makes an un-physical assumption.
We begin with the usual covariant derivative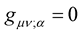 , of Riemann geometry. As alluded, the condition
, of Riemann geometry. As alluded, the condition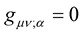 , is the sacrosanct foundation stone of Riemann geometry. We will uphold this covariant derivative condition under the Weyl conformal transformation
, is the sacrosanct foundation stone of Riemann geometry. We will uphold this covariant derivative condition under the Weyl conformal transformation 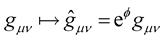 of the metric, i.e.
of the metric, i.e.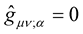 . Likewise, the condition
. Likewise, the condition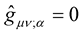 , is to be taken as the sacrosanct foundation stone of the New Weyl Geometry. Written in full, the Equation
, is to be taken as the sacrosanct foundation stone of the New Weyl Geometry. Written in full, the Equation 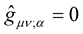 is given by:
is given by:
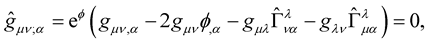 (15)
(15)
and taking4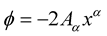 , this equation can be rewritten as:
, this equation can be rewritten as:
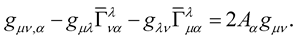 (16)
(16)
As is the case with Professor Weyl’s original geometry, the covariant derivative 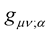 does not vanish since
does not vanish since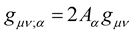 . With this, just like Weyl, we have achieved the non-Riemann geometry so desired.
. With this, just like Weyl, we have achieved the non-Riemann geometry so desired.
Now, we have to calculate the resulting affine connections and for this, we have to write down the three expressions that result from a cyclic permutation of the indices 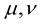 and
and 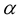 in
in 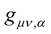 and
and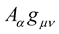 , that is:
, that is:
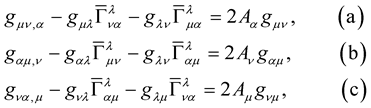 (17)
(17)
where the “bar” on 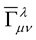 has been put so that it is made clear that this affine is neither Christoffel symbol nor the usual Weyl connection
has been put so that it is made clear that this affine is neither Christoffel symbol nor the usual Weyl connection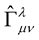 , but the is the new Weyl connection of the new Weyl geometry.
, but the is the new Weyl connection of the new Weyl geometry.
Now, as before, subtracting from Equation (17a) the sum of (17b) and (17c), one obtains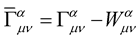 , where—as before,
, where—as before, 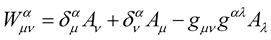 and
and 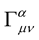 are the usual Weyl tensor and Christoffel three symbol of Riemann geometry respectively. The geometry that we have just described is what we shall call the New Weyl Geometry. As is the case with Professor Weyl’s original geometry, this geometry tends to Riemann geometry as
are the usual Weyl tensor and Christoffel three symbol of Riemann geometry respectively. The geometry that we have just described is what we shall call the New Weyl Geometry. As is the case with Professor Weyl’s original geometry, this geometry tends to Riemann geometry as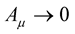 . Further, like in the case of the original Weyl geometry, this geometry is invariant under the same transformations (14).
. Further, like in the case of the original Weyl geometry, this geometry is invariant under the same transformations (14).
If 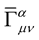 is invariant under the transformation (14) i.e.
is invariant under the transformation (14) i.e.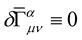 , the curvature tensor
, the curvature tensor 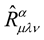 is also invariant i.e.
is also invariant i.e.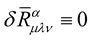 . At this point we have successfully recast Weyl’s theory into a new theory where we have up to now not worried about the change of length of vectors. The factor 2 in (14a), i.e. in the exponential function
. At this point we have successfully recast Weyl’s theory into a new theory where we have up to now not worried about the change of length of vectors. The factor 2 in (14a), i.e. in the exponential function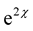 , is necessary in-order that
, is necessary in-order that 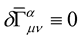 and the reasons are as follows.
and the reasons are as follows.
It should be noted that in Riemann geometry, the metric is constrained such that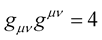 . This property carries over into the New Weyl Geometry, i.e.
. This property carries over into the New Weyl Geometry, i.e.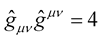 . Since
. Since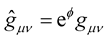 , it follows that for
, it follows that for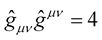 , we must have
, we must have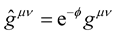 . From these invariable facts, it follows that:
. From these invariable facts, it follows that:
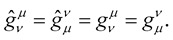 (18)
(18)
These properties of the metrics 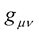 and
and 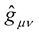 described above also apply to the original Weyl geometry, or Weyl’s old theory.
described above also apply to the original Weyl geometry, or Weyl’s old theory.
Clearly, the geometry just described is a hybrid Riemann geometry and the reason for saying this is because it is Riemann in all its mathematical structure, but it not Riemann in its nature. In the next section, we now demonstrate the trivial but the sort for fact, namely that, this hybrid Riemann geometry or New Weyl Geometry preserves lengths.
6. Defence to Weyl’s Geometry
Now, under the New Weyl Geometry, the change of length of a vector has the same form and structure as happens in Riemann geometry i.e. (4) albeit with the conformal Weyl transformation (6) effected to the metric 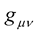 in (4), i.e.:
in (4), i.e.:
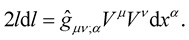 (19)
(19)
Now, given that we have set the foundation stone of the New Weyl Geometry to be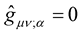 , it follows that
, it follows that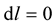 . Einstein’s valid criticism is invalidated, it is reduced to naught, it falls apart into nothing but shreds—it comes out flying through the window!
. Einstein’s valid criticism is invalidated, it is reduced to naught, it falls apart into nothing but shreds—it comes out flying through the window!
At a stroke, in this very trivial way, the great Professor Weyl could have thwarted the great Professor Einstein. The problem is that Professor Weyl set the Weyl hypothesis (7) as the foundation stone of his theory, it is this that he made the great endeavour to defend. With hindsight, we now see that what Professor Weyl should have defended is not (7) but the invariance of the connection 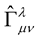 under the transformations (14) because it is these that guarantee the inclusion of the electromagnetic field into the framework of gravitation and not the Weyl hypothesis (7).
under the transformations (14) because it is these that guarantee the inclusion of the electromagnetic field into the framework of gravitation and not the Weyl hypothesis (7).
7. Discussion and Conclusion
Without any doubt, Professor Weyl produced the first Natural Unified Field Theory for which the Maxwellian electromagnetic field 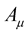 and the gravitational field
and the gravitational field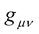 , appear side-by-side as geometrical properties of the fabric space-time and regrettably, for simple reasons of incredulity cast by Einstein’s agile intellect, the theory largely lies forgotten. To say Professor Weyl’s theory lies forgotten is not a correct representation of the state of affairs. Perhaps the correct statement to say is that “Professor Einstein’s criticism continues—today as it did on the first day of its pronouncement; to hover above Professor Weyl’s theory so much that no physically meaningful results can be derived from it as one must first overcome Einstein’s spell over it”.
, appear side-by-side as geometrical properties of the fabric space-time and regrettably, for simple reasons of incredulity cast by Einstein’s agile intellect, the theory largely lies forgotten. To say Professor Weyl’s theory lies forgotten is not a correct representation of the state of affairs. Perhaps the correct statement to say is that “Professor Einstein’s criticism continues—today as it did on the first day of its pronouncement; to hover above Professor Weyl’s theory so much that no physically meaningful results can be derived from it as one must first overcome Einstein’s spell over it”.
However, despite Professor Einstein’s criticism, 95 years on, research into Professor Weyl’s theory—while not very active, it is much alive see e.g. [10] [11]and reference therein]. By active, we mean it is not embraced universally by the majority but is only take-up for academic reasons largely to do with curiosity than to do with seeking solid answers to the nature of physical and natural reality. That said, interesting to note is that Professor Weyl’s theory was not, and never has been, disproved, but only sidelined because of Einstein’s venomous and lethal criticism.
Now, since what we have done herein is to show that Professor Einstein’s criticism can be thrown out of the window, we are left wondering what becomes of Professor Weyl’s theory now? Is it acceptable now simple because its greatest setback has been overcome? To ourself, we feel this only opens the doors for exploration of this theory without any worry of Professor Einstein’s haunting criticism.
However, one fact that is likely to continue to haunt the theory is that it is not a true unification of gravitation and electricity as these fields non-mutually and non-intimately sit side-by-side in a disjoint manner and fashion with no obvious and clearly visible connection to one another. That is to say, unlike in the case of electricity and magnetism, there is no reciprocal action between the two fields 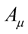 and
and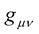 . This is a great setback for those seeking true unification were reciprocal action between fields is assumed to be the sure hallmark of unification.
. This is a great setback for those seeking true unification were reciprocal action between fields is assumed to be the sure hallmark of unification.
In-closing, allow us to say that perhaps as a way of demonstrating what development can spring from the new Weyl geometry that we have just proposed, we shall in §(7.2) put down some of our thoughts on this. These thoughts form part a future monograph where we develop this new geometry into a fully-fledge unified theory of all the fundamental forces of Nature.
7.1. Conclusion
As demonstrated herein, a Weyl geometry completely free from Professor Einstein’s criticism is possible. This geometry preserves the lengths of vectors and maintains a four vector field as in Professor Weyl’s original theory. This four vector field together with the gravitational field submit to Professor Weyl’s original gauge transformation of these two fields thus allowing one to identify the four vector field with the electromagnetic field as Professor Weyl did in his original presentation.
7.2. Future Thoughts
We certainly have defended Professor Weyl’s inclusion of the four vector 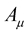 by rendering obsolete Professor Einstein’s criticism. The question that immediately comes to mind is what use can this new geometry be insofar as current effort of unifying all the four fundamental forces is concerned? First and foremost is that development of Professor Weyl’s theory can now proceed without the thick dark cumulonimbus cloud cast upon it by Professor Einstein. Be that it may, one major set back likely to be faced by such attempts is the same problem that the original Weyl theory faces, namely, the problem that the gravitational and electromagnetic phenomenon sit side-by-side with no real intimate and reciprocal action as is to be expected of a unified theory e.g. the intimate and reciprocal action between electricity and magnetism in Maxwellian electrodynamics—this is the envisaged intimate and reciprocal action between gravitation and the electrodynamic phenomenon. It should be said that our feeling about what the final unified theory must, only come in as a guide. The ultimate theory that corresponds with reality may not have this intimate and reciprocal action that we hope for.
by rendering obsolete Professor Einstein’s criticism. The question that immediately comes to mind is what use can this new geometry be insofar as current effort of unifying all the four fundamental forces is concerned? First and foremost is that development of Professor Weyl’s theory can now proceed without the thick dark cumulonimbus cloud cast upon it by Professor Einstein. Be that it may, one major set back likely to be faced by such attempts is the same problem that the original Weyl theory faces, namely, the problem that the gravitational and electromagnetic phenomenon sit side-by-side with no real intimate and reciprocal action as is to be expected of a unified theory e.g. the intimate and reciprocal action between electricity and magnetism in Maxwellian electrodynamics—this is the envisaged intimate and reciprocal action between gravitation and the electrodynamic phenomenon. It should be said that our feeling about what the final unified theory must, only come in as a guide. The ultimate theory that corresponds with reality may not have this intimate and reciprocal action that we hope for.
Now, in the new Weyl geometry just proposed, if we are to identify the object 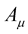 not as a vector but are to demand of this object that it allows us to attain tensorial affines, then, we have to make the asymptotic transformation in our thinking about this object, whereby
not as a vector but are to demand of this object that it allows us to attain tensorial affines, then, we have to make the asymptotic transformation in our thinking about this object, whereby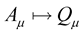 , such that:
, such that:
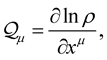 (20)
(20)
where the object 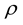 is defined such that:
is defined such that:
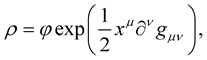 (21)
(21)
where 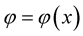 is some scalar. In this way, the affine connection
is some scalar. In this way, the affine connection 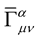 transforms into a tensor, i.e.:
transforms into a tensor, i.e.:
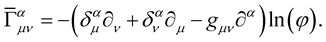 (22)
(22)
What the choice (21) informs us is that it is possible to have a tensorial affine in this new geometry. The major problem with this choice (21) is that it leads us to just one field equation namely,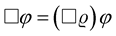 . This situation arises because the affine (22) does not have the metric tensor
. This situation arises because the affine (22) does not have the metric tensor 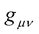 as an intrinsic dependent. We can improve on this choice by making a better choice, namely:
as an intrinsic dependent. We can improve on this choice by making a better choice, namely:
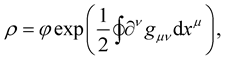 (23)
(23)
where the line integral is such that:
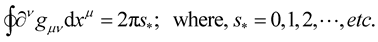 24)
24)
In this way, the derivatives of the line integral vanish identically, i.e.:
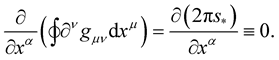 (25)
(25)
As will become clear soon, this vanishing of the line integral is handy as it allows the metric 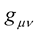 to remain as an intrinsic part of the metric.
to remain as an intrinsic part of the metric.
We must take note of the fact that while 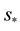 is a constant whole number, it will transform upon a coordinate transformation. To see this, we know that upon a coordinate transformation, we will have:
is a constant whole number, it will transform upon a coordinate transformation. To see this, we know that upon a coordinate transformation, we will have:
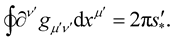 (26)
(26)
The left hand-side of this Equation is such that:
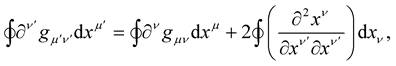 (27)
(27)
and this implies:
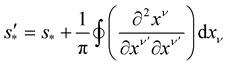 (28)
(28)
Therefore 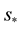 undergoes a change upon a coordinate transformation. In this way, the tensorial affine
undergoes a change upon a coordinate transformation. In this way, the tensorial affine 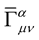 will now have the metric as an intrinsic dependent, i.e.:
will now have the metric as an intrinsic dependent, i.e.:
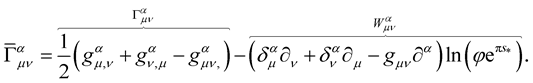 (29)
(29)
The extra-terms that accompany 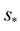 upon a coordinate transformation are cancelled identically by the nontensor terms that emerge from the affine
upon a coordinate transformation are cancelled identically by the nontensor terms that emerge from the affine 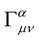 upon a coordinate transformation. In is way, the number
upon a coordinate transformation. In is way, the number 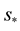 can be considered to be a non-changing and intrinsic property of the particle.
can be considered to be a non-changing and intrinsic property of the particle.
At this point, we are ready to take our next step. We know that the corresponding curvature tensor for the new Weyl geometry is:
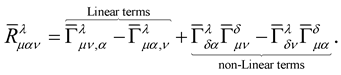 (30)
(30)
Now, given that we have attained a geometry with tensorial affines—a geometry that e.g. Professor Einstein [12] and Professor Schrödinger [13]-[15]sought; one can take the fullest advantage of the tensorial nature of the affinities because we now have the mathematical and physical prerogative, legitimacy and above all, the liberty to choose a spacetime where the non-linear terms vanish identically i.e., a spacetime such that, 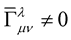 , while at the sametime these affinities are such that:
, while at the sametime these affinities are such that:
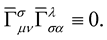 (31)
(31)
Clearly and without any doubt, this fact that we have chosen a spacetime that is governed by the constraint (31), this means that we have just reed ourself of the monstrous and troublesome non-linear terms in the Riemann tensor (30) because with this beautiful and elegant choice (31), they [the non-linear terms] now vanish identically. This means (30) now becomes:
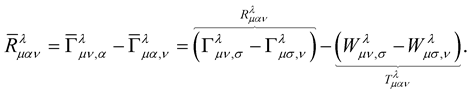 (32)
(32)
that is to say:
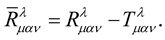 (33)
(33)
The tensor 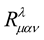 is the usual Riemann tensor while
is the usual Riemann tensor while 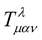 is a tensor that is a function of the scalar
is a tensor that is a function of the scalar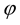 . If this scalar is associated with the wavefunction of the particle, then, the
. If this scalar is associated with the wavefunction of the particle, then, the 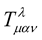 can be thought of as a material tensor. Actually—in the up-coming monograph were we take this work to much greater heights, this is what we take it to be—a material tensor in same manner as
can be thought of as a material tensor. Actually—in the up-coming monograph were we take this work to much greater heights, this is what we take it to be—a material tensor in same manner as 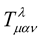 is a material tensor in Professor Einstein’s general relativity.
is a material tensor in Professor Einstein’s general relativity.
Now, as is well known, Riemann geometry does not preserve the angles but only the length of the vector under parallel transport. The only way to have both the angles and the length preserved is if the affinities are tensors and the curvature tensor of such a spacetime will be identically equal to zero. To see this, we know that under parallel transport, the directional change of a vector will be given by:
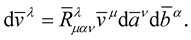 (34)
(34)
If as we desire—that both the length and angle are preserved under parallel transport; we must have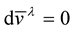 . This fact that,
. This fact that, 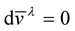 , implies that
, implies that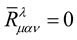 . Given (33), it follows follows from this that:
. Given (33), it follows follows from this that:
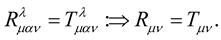 (35)
(35)
At this point—it turns out that we have just derived the material tensor from pure geometry and not to insert it by the sleight of the mind and hand as he [Einstein] did with his gravitational field equation. As his internationally acclaimed scientific biographer Professor Abraham Pais graphically put it—Professor Einstein would look at his Equation, i.e.:
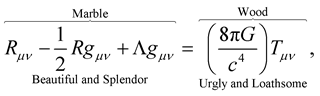 (36)
(36)
and greatly admire the left hand side which he would compare with marble—it was beautiful, pure and was a marvel sight for the artist as it was constructed from pure geometry; but when he [Professor Einstein] would look at the right hand side of this same equation; with equal passion, he was visited by deep melancholy sighs and feelings which made him loath the right hand side of his equation—he would compare this right handside with wood— it was ugly; with no end insight, Professor Einstein would moan time and again.
His ultimate pine and goal thereof was to turn wood into marble, which meant deriving the material field from pure geometry. Professor Einstein wanted to find the final theory, thus he pursued to the very end of life to a point that while on his death death on April 13, 1955, he asked for a pen and his notes so that he could work on the unified theory that he was working on at the time. Without an iota of doubt, if what is before us proves itself to have a correspondence with physical and natural reality, then we can safely say we have achieved one of Professor Einstein’s goals to attaining the “Elicit Dream of a Final Theory” by deriving the material tensor from pure geometry—wood has finally been turned into marble!
In closing, allow us to say that what we have presented in this section is but a miniature snapshot of things to come. In an up-coming monograph spanning nearly 200 pages and most certainly to be published by World Scientific Publishers Inc., we have developed the new Weyl geometry into a unified theory of all the four forces. This theory unifies not only the four forces, but quantum and classical physics as well.
NOTES
1See e.g. http://plato.stanford.edu/entries/weyl/

2[Abraham Pais in Ref. Subtle is the Lord, p. 341]
3[Ref. in Sidelights of Relativity, p. 23]

4In the original Weyl theory, the scaler 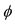 is such that
is such that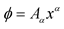 . In the recast Weyl theory, we have chosen that
. In the recast Weyl theory, we have chosen that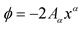 . There is nothing special about the introduction of the negative 2 in the scaler
. There is nothing special about the introduction of the negative 2 in the scaler 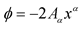 except that it has been done for convenience.
except that it has been done for convenience.