Banach Λ-Frames for Operator Spaces

Mukesh Singh, Renu Chugh

Department of Mathematics, Goverment College, Bahadurgarh, India.
Department of Mathematics, Maharishi Dayanand University, Rohtak, India.

DOI: 10.4236/apm.2014.48048                

Abstract

The Banach frame for a Banach space X can reconstruct each vector in X by the pre-frame operator or the reconstruction operator. The Banach Λ-frame for operator spaces was introduced by Kaushik, Vashisht and Khattar [Reconstruction Property and Frames in Banach Spaces, Palestine Journal of Mathematics, 3(1), 2014, 11-26]. In this paper we give necessary and sufficient conditions for the existence of the Banach Λ-frames. A Paley-Wiener type stability theorem for Λ-Banach frames is discussed.

Keywords

Frames, Banach Frames, Reconstruction Property, Perturbation

1. Introduction

Duffin and Schaeffer in [1] while working in nonharmonic Fourier series developed an abstract framework for the idea of time-frequency atomic decomposition by Gabor [2] and defined frames for Hilbert spaces. In 1986, Daubechies, Grossmann and Meyer [3] found new applications to wavelets and Gabor transforms in which frames played an important role.

Let 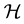be an infinite dimensional separable complex Hilbert space with inner product. A system 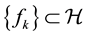is a frame (Hilbert) for 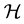if there exist positive constants A and B such that

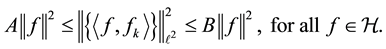(1.1)

The positive constants A and B are called the lower and upper bounds of the frame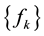, respectively. They are not unique. The inequality (1.1) is called the frame inequality of the frame.

Gröchenig in [4] generalized Hilbert frames to Banach spaces. Before the concept of Banach frames was formalized, it appeared in the foundational work of Feichtinger and Gröchenig [5] [6] related to the atomic decompositions. Atomic decompositions appeared in the field of applied mathematics providing many applications [7] . An atomic decomposition allows a representation of every vector of the space via a series expansion in terms of a fixed sequence of vectors which we call atoms. On the other hand Banach frames for a Banach space ensure reconstruction via a bounded linear operator or the synthesis operator.

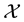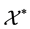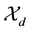Definition 1.1. [4] . Let be a Banach space, the conjugate space of and let be an asso-

ciated Banach space of scalar valued sequences. A pair 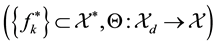is called a Ba-

nach frame for with respect to an associated sequence space if

1), for each.

2) There exist positive constants such that

3) is a bounded linear operator operator such that.

In the later half of twentieth century, Coifman and Weiss in [8] introduced the notion of atomic decomposition for function spaces. Later, Feichtinger and Gröchenig [5] [6] extended this idea to Banach spaces. This concept was further generalized by Gröchenig [4] , who introduced the notion of Banach frames for Banach spaces. Casazza, Han and Larson [9] also carried out a study of atomic decompositions and Banach frames. For recent development in frames for Banach spaces one may refer to [10] -[17] . Recently, various generalizations of frames in Banach spaces have been introduced and studied. Han and Larson [18] defined a Schauder frame for a Banach space to be an inner direct summand (i.e. a compression) of a Schauder basis of. The reconstruction property in Banach spaces was introduced and studied by Casazza and Christensen in [19] and further studied in [20] -[23] . The basic theory of frames can be found in [24] -[26] .

Definition 1.2. [19] . Let be a separable Banach space. A sequence has the reconstruction property for with respect to a sequence if

(1.2)

In short, we will say that the pair has the reconstruction property for. More precisely, we say that is a reconstruction system or the reconstruction property for.

The reconstruction property is an important tool in several areas of mathematics and engineering. The reconstruction property is also used to study the geometry of Banach spaces. In fact, it is related to the bounded approximated property as observed in [9] [27] .

Recently, Kaushik et al. in [20] introduced Banach Λ-frame for operator spaces while working in the reconstruction property in Banach spaces. In this paper we give necessary and sufficient conditions for the existence of Banach Λ-frames for operator spaces. A Paley-Wiener type stability theorem for Λ-Banach frames is dis- cussed.

2. Banach Λ-Frames

The reconstruction property in Banach spaces is a source of other redundant systems! For example, if has the reconstruction property for with respect to. Then, we can find a reconstruction operator such that is a Banach frame for. The Banach frame is called the associated Banach frame for the underlying space. Similarly we can find a reconstruction operator associated with the system. It is natural to ask whether we can find Banach frames for a large class of spaces associated with a given reconstruction system. In this direction the Banach Λ-frames for the operator spaces introduced in [20] . First recall that the family of all bounded linear operator from a Banach space into a Banach space is denoted by. If, then we write. An operator is said to be coercive if there exists such that for all.

Definition 2.1. [20] . Let and be Banach spaces and let be a sequence space associated with. A sequence is a Banach Λ-frame for if there exist positive constants such that

(2.1)

If upper inequality in (2.1) is satisfied, then is called a Λ-Bessel sequence for with Bessel bound B₀. The operator given by, is called the pre-frame operator and the analysis operator is given by

The positive constants, are called the lower and upper frame bounds of the Banach Λ-frame, respectively. If the removal of any from the Banach Λ-frame renders the collection to be a Banach Λ-frame for the underlying space, then is said to be an exact Banach Λ-frame.

Remark 2.2. If, then. Therefore, becomes a Banach frame for with respect to the associated Banach space.

Suppose that has the reconstruction property for with respect to where. Let be a Banach space and let

be its associated Banach space of sequences with the norm given by

Then, is a Banach Λ-frame for the operator space with respect to. There may be other sequence spaces with respect to which form a Banach frame for the underlying space. The following theorem provides existence of the Banach Λ-frame for the operator spaces (see [20] ). We give the proof for the completeness.

Theorem 2.3. [20] . Suppose that has the reconstruction property for with respect to. Then, is a Banach Λ-frame for the operator space with respect to.

Proof. Let be arbitrary. For each, define by

Then

Thus, , for all. Therefore, by using the Banach-Steinhaus Theorem, we have.

Fix. Then,

(2.2)

Also for all, we have

(2.3)

Therefore, by using (2.3) we obtain.

This gives

(2.4)

By using (2.2) and (2.4) with, we have

Hence is a Banach Λ-frame for the operator space with respect to. This completes the proof. □

The following theorem gives necessary and sufficient conditions for to be a Λ-Banach frame for with respect to an associated Banach space of scalar valued sequences.

Theorem 2.4. A sequence is a Banach Λ-frame for with respect to which is generated by if and only if is isomorphic to a closed subspace of.

Proof. Assume that is Banach Λ-frame for with respect to. Then, there exist positive constants A, B such that

(2.5)

By using lower frame inequality in (2.5), the analysis operator T of is coercive. Thus T is injective and has close range. From the Inverse Mapping Theorem, is isomorphic to the range, which is a subspace of. For the reverse part, assume that M is a closed subspace of and U is an isomorphic from onto M. Let be the sequence coordinate operators on, then for all.

Choose,. Then, for all we have

Therefore

Hence is Banach Λ-frame for with respect to. □

Theorem 2.5. A sequence is a Banach Λ-frame for if and only if is isomor- phic to a complemented subspace of which is generated by.

Proof. Assume first that is Banach Λ-frame for and let T is the analysis operator and S is the synthesis operator for the Banach Λ-frame. Then, is the identity operator on. Choose. Then, and. Therefore, P is the projection from to the range of T. Thus, is an isomorphism and is complemented subspace of.

For the reverse part, if is an isomorphism, where is the complemented subspace of. Then, by Theorem 2.4, the sequence is a Banach Λ-frame for. □

2.1. Construction of Banach Λ-Frames from Operators on

Let ba a Banach Λ-frame for and let. Let be such that

,. Then, is a Λ-Bessel sequence for, but in general, not

a Banach Λ-frame for.

The following theorem provides necessary and sufficient conditions for the construction of a Banach Λ-frame from a bounded linear operator on.

Theorem 2.6. Let ba a Banach Λ-frame for and let be such that , where. Then, is a Banach Λ-frame for if and only if

where is a positive constant and is such that,.

Proof. Assume first that is a Banach Λ-frame for with bounds,. Let and be the pre-frame operator and analysis operator associated with, respectively. Choose. Then, is such that,. Let be the pre-frame operator associated

with Banach Λ-frame. Choose. Then, for all we have

For the reverse part, we compute

Hence is a Banach Λ-frame for with bounds and. □

The following theorem gives the better Λ-Bessel bound for the sum of two Banach Λ-frames.

Theorem 2.7. Let and be Banach Λ-frames for with respect to and let be an invertible operator such that,. Then, is a Λ-Bessel sequence with bound

where, are the analysis operators associated with and, respectively and is the identity operator on.

Proof. For all, we have

Similarly, we can show that

Hence is a Λ-Bessel sequence with required Bessel bound. □

Remark 2.8. The Λ-Bessel sequence in Theorem 2.7, in general, not a Banach Λ-frame for. If the analysis operator associated with the Λ-Bessel sequence is coercive, then a Λ-Bessel sequence turns out to be a Banach Λ-frame for the underlying space. This is summarized in the following lemma.

Lemma 2.9. Let be Λ-Bessel sequence for. Then is a Banach Λ-frame for if and only if its analysis operator is coercive.

The following theorem gives a relation between the bounds of a Banach Λ-frame and Bessel bound for a Λ-Bessel sequence such that becomes a Banach Λ-frame for.

Theorem 2.10. Let be a Banach Λ-frame for with bounds A, B and let be a Λ-Bessel sequence for with bound, then is a Banach Λ-frame for.

Proof. Suppose that T and R are analysis operators associated with and for. For any, we have

Thus, is a Λ-Bessel sequence for.

Now

Hence is a Banach Λ-frame for. □

Given a Banach Λ-frame for, we now give an estimate of the Bessel bound for such that becomes a Banach Λ-frame for. This is given in the following proposition.

Proposition 2.11. Assume that is a Banach Λ-frame for with respect to. Let be a sequence such that is a Λ-Bessel sequence for with respect to with Bessel bound, where S is the pre-frame operator associated with. Then, is a Banach Λ-frame for.

Proof. We compute

Hence is a Banach Λ-frame for. □

2.2. Perturbation of Λ-Banach Frames

Perturbation theory is a very important tool in various areas of applied mathematics [7] [19] [28] . In frame theory, it began with the fundamental perturbation result of Paley and Wiener. The basic of Paley and Wiener is that a system that is sufficient close to an orthonormal system (basis) in a Hilbert space also forms an orthonormal system (basis). Since then, a number of variations and generalization of this perturbation to the setting of Banach space and then to perturbation of the atomic decompositions, frames (Hilbert)and Banach frames, the reconstruction property in Banach spaces [19] [20] . The following theorem gives a Paley-Wiener type perturbation (in Banach space setting) for Λ-Banach frames.

Theorem 2.12. Let be a Banach Λ-frame for with bounds A, B and let. As-

sume that are non-negative real number such that and

(2.6)

where T and R are the analysis operators associated with and, respectively. Then, is a

Banach Λ-frame for with bounds and.

Proof. For any, we have

Since

(2.7)

By using (2.6) and (2.7), we have

(2.8)

Now

(2.9)

By using (2.6) and (2.9), we have

(2.10)

Therefore, by using (2.8) and (2.10) we conclude that is a Banach Λ-frame for with desired frame bounds. □

Remark 2.13. For other types of perturbation results one may refer to [11] , which can be generalized to Banach Λ-frame for.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Duffin, R.J. and Schaeffer, A.C. (1952) A Class of Non-Harmonic Fourier Series. Transactions of the American Mathematical Society, 72, 341-366. http://dx.doi.org/10.1090/S0002-9947-1952-0047179-6
[2]	Gabor, D. (1946) Theory of Communications. Journal of the Institute of Electrical Engineers, 93, 429-457.
[3]	Daubechies, I., Grossmann, A. and Meyer, Y. (1986) Painless Non-Orthogonal Expansions. Journal of Mathematical Physics, 27, 1271-1283. http://dx.doi.org/10.1063/1.527388
[4]	Grochenig, K. (1991) Describing Functions: Atomic Decompositions versus Frames. Monatshefte für Mathematik, 112, 1-41. http://dx.doi.org/10.1007/BF01321715
[5]	Feichtinger, H. and Grochenig, K. (1989) Banach Spaces Related to Integrable Group Representations and Their Atomic Decompositions I. Journal of Functional Analysis, 86, 307-340. http://dx.doi.org/10.1016/0022-1236(89)90055-4
[6]	Feichtinger, H. and Grochenig, K. (1989) Banach Spaces Related to Integrable Group Representations and Their Atomic Decompositions II. Monatshefte für Mathematik, 108, 129-148. http://dx.doi.org/10.1007/BF01308667
[7]	Christensen, O. and Heil, C. (1997) Pertubation of Banach Frames and Atomic Decompositions. Mathematische Nachrichten, 185, 33-47. http://dx.doi.org/10.1002/mana.3211850104
[8]	Coifman, R.R. and Weiss, G. (1977) Expansions of Hardy Spaces and Their Use in Analysis. Bulletin of the American Mathematical Society, 83, 569-645. http://dx.doi.org/10.1090/S0002-9904-1977-14325-5
[9]	Casazza, P.G., Han, D. and Larson, D.R. (1999) Frames for Banach Spaces. Contemporary Mathematics, 247, 149-182. http://dx.doi.org/10.1090/conm/247/03801
[10]	Jain, P.K., Kaushik, S.K. and Vashisht, L.K. (2006) On Banach Frames. Indian Journal of Pure and Applied Mathematics, 37, 265-272.
[11]	Jain, P.K., Kaushik, S.K. and Vashisht, L.K. (2007) On Stability of Banach Frames. Bulletin of the Korean Mathematical Society, 44, 73-81. http://dx.doi.org/10.4134/BKMS.2007.44.1.073
[12]	Chugh, R., Singh, M. and Vashisht, L.K. (2014) On Λ-Type Duality of Frames in Banach Spaces. International Journal of Analysis and Applications, 4, 148-158.
[13]	Vashisht, L.K. (2012) On Retro Banach Frames of Type P. Azerbaijan Journal of Mathematics, 2, 82-89.
[14]	Vashisht, L.K. (2012) On Φ-Schauder Frames. TWMS Journal of Applied and Engineering Mathematics (JAEM), 2, 116-120.
[15]	Vashisht, L.K. (2012) On Frames in Banach Spaces. Communications in Mathematics and Applications, 3, 313-332.
[16]	Vashisht, L.K. and Sharma, S. (2012) On Weighted Banach Frames. Communications in Mathematics and Applications, 3, 283-292.
[17]	Vashisht, L.K. and Sharma, S. (2014) Frames of Eigenfunctions Associated with a Boundary Value Problem. International Journal of Analysis, 2014, Article ID: 590324. http://dx.doi.org/10.1155/2014/590324
[18]	Han, D. and Larson, D.R. (2000) Frames, Bases and Group Representations. Memoirs of the American Mathematical Society, 147, 1-91.
[19]	Casazza, P.G. and Christensen, O. (2008) The Reconstruction Property in Banach Spaces and a Perturbation Theorem. Canadian Mathematical Bulletin, 51, 348-358. http://dx.doi.org/10.4153/CMB-2008-035-3
[20]	Kaushik, S.K., Vashisht, L.K. and Khattar, G. (2014) Reconstruction Property and Frames in Banach Spaces. Palestine Journal of Mathematics, 3, 11-26.
[21]	Khattar, G. and Vashisht, L.K. (2014) The Reconstruction Property in Banach Spaces Generated by Matrices. Advances in Pure and Applied Mathematics, 5, 151-160.
[22]	Khattar, G. and Vashisht, L.K. (2014) Some Types of Convergence Related to the Reconstruction Property in Banach Spaces. Submitted.
[23]	Vashisht, L.K. and Khattar, G. (2013) On -Reconstruction Property. Advances in Pure Mathematics, 3, 324-330. http://dx.doi.org/10.4236/apm.2013.33046
[24]	Casazza, P.G. and Kutynoik, G. (2012) Finite Frames. Birkhauser.
[25]	Heil, C. and Walnut, D. (1989) Continuous and Discrete Wavelet Transforms. SIAM Review, 31, 628-666. http://dx.doi.org/10.1137/1031129
[26]	Young, R. (2001) A Introduction to Non-Harmonic Fourier Series. Academic Press, New York.
[27]	Casazza, P.G. (2001) Approximation Properties. In: Johnson, W.B. and Lindenstrauss, J., Eds., Handbook on the Geometry of Banach Spaces, Vol. I, 271-316.
[28]	Casazza, P.G. and Christensen, O. (1997) Perturbation of Operators and Applications to Frame Theory. Journal of Fourier Analysis and Applications, 3, 543-557. http://dx.doi.org/10.1007/BF02648883