A Mathematical Model to Solve Bio-Heat Transfer Problems through a Bio-Heat Transfer Equation with Quadratic Temperature-Dependent Blood Perfusion under a Constant Spatial Heating on Skin Surface ()
1. Introduction
Using the Pennes bio-heat transfer (BHT) equation [1] which accounts for the ability of tissue to remove heat by both passive conduction and perfusion of tissue by blood, many of the bio-heat transfer problems have been modelled. The BHT equation defines the thermal behavior of tissue and includes four terms that influence the heat transfer at the tissue surface: the heat exchange between the tissue surface and the environment, the conduction through the tissue, the energy transfer by blood circulation in the tissue, and the heat generation due to local metabolism. The contributions of heat conduction and perfusion are combined in the Pennes bio-heat equation [1] [2] , that we use in a form that employs 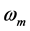 [3]
[3]
 (1.1)
(1.1)
Here,  ,
,  and
and 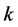 are the density, specific heat, and thermal conductivity of tissue, respectively,
are the density, specific heat, and thermal conductivity of tissue, respectively,  is the specific heat of blood,
is the specific heat of blood,  is the density of blood,
is the density of blood,  is local tissue temperature,
is local tissue temperature, 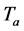 is the arterial blood temperature,
is the arterial blood temperature, 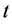 is the time,
is the time,  is the metabolic heat generation rate per unit volume,
is the metabolic heat generation rate per unit volume, 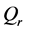 is the heat deposited per volume due to spatially distributed heating, and
is the heat deposited per volume due to spatially distributed heating, and  is the blood perfusion rate. The BHT model (1.1) can be used for the quantitative diagnostics of physiological conditions on biological bodies, as for example, for simulations of regional hyperthermia for cancer therapy [3] -[5] . For thermal problems, Equation (1.1) is subject to the usual boundary conditions 1) temperature prescribed,
is the blood perfusion rate. The BHT model (1.1) can be used for the quantitative diagnostics of physiological conditions on biological bodies, as for example, for simulations of regional hyperthermia for cancer therapy [3] -[5] . For thermal problems, Equation (1.1) is subject to the usual boundary conditions 1) temperature prescribed, 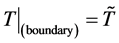 , where (boundary) is either the whole or a part of the boundary of domain
, where (boundary) is either the whole or a part of the boundary of domain ; or 2) heat flux prescribed,
; or 2) heat flux prescribed,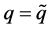 ; or 3) convection,
; or 3) convection,
 , where
, where  is the heat transfer coefficient and
is the heat transfer coefficient and  is the temperature of the surrounding medium; or radiation,
is the temperature of the surrounding medium; or radiation,  , where
, where  is the Stefan-Boltzman constant,
is the Stefan-Boltzman constant, 
is the radiative interchange factor between the surface and the exterior ambient temperature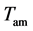 .
.
The parameters considered in Equation (1.1) are usually assumed to be constant except for the blood perfusion, which varies with temperature  to include the specific case of temperature-dependent perfusion [3] -[5] . Perfusion is defined as the nonvectorial volumetric blood flow per tissue volume in a region that contains sufficient capillaries that an average flow description is considered reasonable. Therefore it is expected that the heat dissipation should vary with the blood perfusion rate. Most tissues, including much of the skin and brain, are highly perfused, with a perfusion coefficient denoted by
to include the specific case of temperature-dependent perfusion [3] -[5] . Perfusion is defined as the nonvectorial volumetric blood flow per tissue volume in a region that contains sufficient capillaries that an average flow description is considered reasonable. Therefore it is expected that the heat dissipation should vary with the blood perfusion rate. Most tissues, including much of the skin and brain, are highly perfused, with a perfusion coefficient denoted by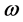 , can be replaced, as in Equation (1.1), by
, can be replaced, as in Equation (1.1), by , the nondirectional mass flow associated with perfusion. One of the most important applications of blood perfusion effects and measurements is tumour detection. Tumours are known to have a different perfusion rate than normal healthy tissue. They are generally highly vascular and so blood flows through them more quickly. Therefore the ability to know the effects and the measurements of this abnormal perfusion rate could help evaluate the size and severity of a tumour. By varying some parameters of the blood perfusion
, the nondirectional mass flow associated with perfusion. One of the most important applications of blood perfusion effects and measurements is tumour detection. Tumours are known to have a different perfusion rate than normal healthy tissue. They are generally highly vascular and so blood flows through them more quickly. Therefore the ability to know the effects and the measurements of this abnormal perfusion rate could help evaluate the size and severity of a tumour. By varying some parameters of the blood perfusion , it is possible to examine the effect that different volume flow rates of blood have on the heat transfer inside the biological bodies.
, it is possible to examine the effect that different volume flow rates of blood have on the heat transfer inside the biological bodies.
The analytical study of Equation (1.1) as a nonlinear evolution equation is of great interest. As in the study of nonlinear physical phenomena, the investigations of the travelling wave solution of Equation (1.1) play an important role in the analytical study of the nonuniform thermal distribution in biological tissues. The importance of obtaining the analytical solutions, if available, of Equation facilitates 1) the investigation of temperature distribution inside the biological bodies, 2) the verification of numerical solvers, and aids in the stability analysis of solutions. In the present work, we aim to find analytical thermal traveling wave solution of one-dimensional (1D) BHT equation
 (1.2)
(1.2)
with a quadratic temperature-dependent blood perfusion [6] -[8]
 (1.3)
(1.3)
where  is the baseline perfusion,
is the baseline perfusion, 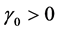 and
and 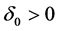 are respectively the linear and quadratic coefficients of temperature-dependence. Here, we assume that the skin surface is defined at
are respectively the linear and quadratic coefficients of temperature-dependence. Here, we assume that the skin surface is defined at  while the body core at
while the body core at 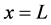 so that
so that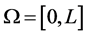 . For the simplicity, we will limit ourselves to the special case of constant spatial heating. This reflects the situation where the human skin was heated by a laser [9] [10] . The analytical solutions will allow us to investigate the effect of the blood perfusion on heat transfer in the tissues. The analytical solutions are obtained with the help of the extended mapping method [11] [12] . The rest of the work is organized as follows. In section 2, we present analytical thermal traveling wave solution of Equation (1.2) with blood perfusion (1.3). The results are discussed in section 3. In section 4, we conclude our work by summarizing the main results.
. For the simplicity, we will limit ourselves to the special case of constant spatial heating. This reflects the situation where the human skin was heated by a laser [9] [10] . The analytical solutions will allow us to investigate the effect of the blood perfusion on heat transfer in the tissues. The analytical solutions are obtained with the help of the extended mapping method [11] [12] . The rest of the work is organized as follows. In section 2, we present analytical thermal traveling wave solution of Equation (1.2) with blood perfusion (1.3). The results are discussed in section 3. In section 4, we conclude our work by summarizing the main results.
2. Thermal Traveling Wave Solutions of the 1D BHT Model with Quadratic Temperature-Dependent Blood Perfusion
In this section, we aim to apply the extended mapping method to find analytical solutions of Equation (1.1) with quadratic temperature-dependent blood perfusion (1.3). For the traveling wave solutions of Equations (1.2), (1.3), we introduce the ansatz
 (1.4)
(1.4)
where  and
and 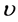 are two real parameters be determined later. Inserting ansatz (1.4) into Equations (1.2), (1.3) yields the ordinary differential equation (ODE)
are two real parameters be determined later. Inserting ansatz (1.4) into Equations (1.2), (1.3) yields the ordinary differential equation (ODE)
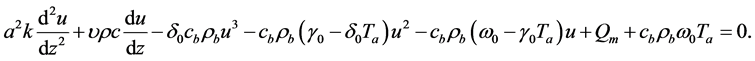 (1.5)
(1.5)
Then, we seek for the solutions of Equation (1.5) in the form [11] [12]
 (1.6)
(1.6)
where 
 are real constants to be determined later,
are real constants to be determined later, 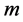 is a positive integer to be determined by balancing the second order derivative and the cubic terms in Equation (1.5), and
is a positive integer to be determined by balancing the second order derivative and the cubic terms in Equation (1.5), and 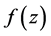 is any solution (satisfying condition
is any solution (satisfying condition  for all
for all  and
and ) of equation
) of equation
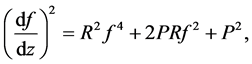 (1.7)
(1.7)
where 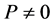 and
and 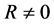 are real are parameters to be determined. It is easily seen that the second hand side of Equation (1.7) is a perfect square so that (1.7) can be solved in the derivative:
are real are parameters to be determined. It is easily seen that the second hand side of Equation (1.7) is a perfect square so that (1.7) can be solved in the derivative: . Each of equations
. Each of equations 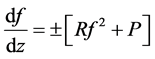 is a Riccati equation and its general solution is known. In what follows, we limit ourselves to only one of these equation (the case of the second equation can be done similarly). Without loss of generality, we consider the equation with sign “
is a Riccati equation and its general solution is known. In what follows, we limit ourselves to only one of these equation (the case of the second equation can be done similarly). Without loss of generality, we consider the equation with sign “ ”,
”,
 (1.8)
(1.8)
Because we are interesting in the solutions  for all
for all  and
and , parameters
, parameters 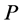 and
and  must satisfy condition
must satisfy condition  Under the condition
Under the condition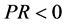 , the general solution of (1.8) is
, the general solution of (1.8) is
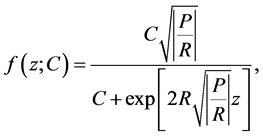 (1.9)
(1.9)
where  is a constant of integration to be particularized from condition either
is a constant of integration to be particularized from condition either  or
or
 ,
, 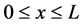 , and
, and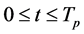 ,
,  being the duration of the heating process.
being the duration of the heating process.
We now turn to the search of different parameters appearing in Equations (1.6), (1.7), and (1.8). Inserting  into Equation (1.5) and balancing the second order derivative and the cubic terms yields
into Equation (1.5) and balancing the second order derivative and the cubic terms yields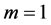 , which in Equation (1.6) leads to
, which in Equation (1.6) leads to
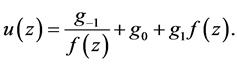 (1.10)
(1.10)
Inserting expression (1.10) for  into Equation (1.6) and equating to zero the coefficients of different powers of
into Equation (1.6) and equating to zero the coefficients of different powers of  leads to the following nonlinear algebraic system
leads to the following nonlinear algebraic system
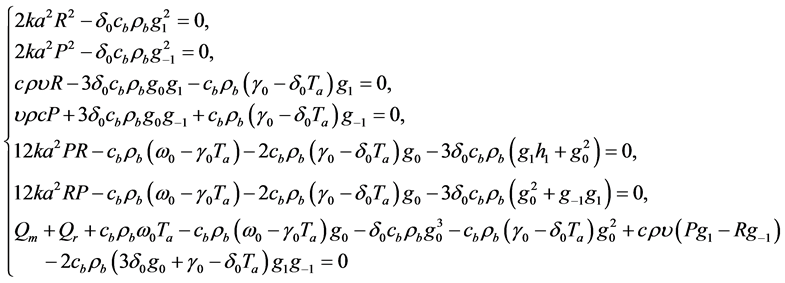 (1.11)
(1.11)
for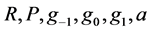 , and
, and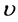 . Solving system (1.11) yield
. Solving system (1.11) yield
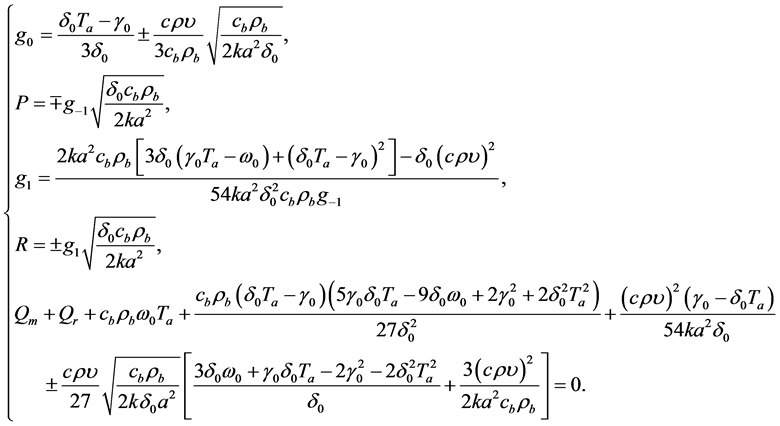 (1.12)
(1.12)
It should be noted that
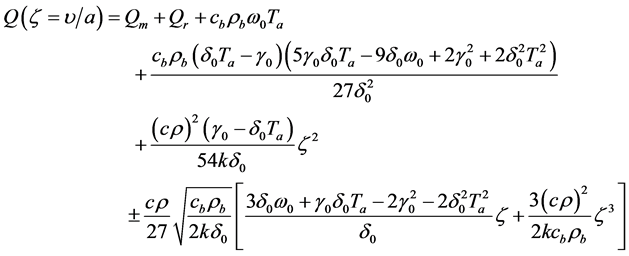
is a third degree polynomial with respect to , so that the last equation in system (1.12) always admits at least one real solution in
, so that the last equation in system (1.12) always admits at least one real solution in . It is important to point out that solutions (1.12) contain two arbitrary real parameters,
. It is important to point out that solutions (1.12) contain two arbitrary real parameters,  and
and . Inserting the expressions for
. Inserting the expressions for  and
and  into Equation (1.9) yields
into Equation (1.9) yields
 (1.13)
(1.13)
and condition  becomes
becomes
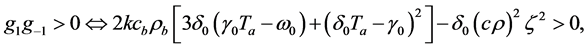 (1.14)
(1.14)
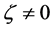 being any real zero of polynomial
being any real zero of polynomial . Therefore, solution (1.13) is associated with only those zeros
. Therefore, solution (1.13) is associated with only those zeros  of polynomial
of polynomial 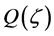 satisfying condition (1.14). As it has been mentioned above, parameter
satisfying condition (1.14). As it has been mentioned above, parameter  of solution (1.13) must be particularized from condition either
of solution (1.13) must be particularized from condition either  or
or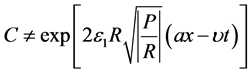 ,
,
 and
and ,
,  being the duration of the heating process. Inserting Equation (1.13) into Equation (1.10) and going back to variables
being the duration of the heating process. Inserting Equation (1.13) into Equation (1.10) and going back to variables  and
and  lead to the following analytical solution of Equations (1.2), (1.3)
lead to the following analytical solution of Equations (1.2), (1.3)
 (1.15)
(1.15)
From what have being saying above, it is clear that solution (1.15) contains three parameters, 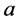 ,
,  , and
, and 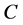 That may be determined using boundary conditions associated with Equations (1.2), (1.3). For example, if the biological tissue is exposed to the environment then the transfer of heat between the skin surface and environment is due to conduction, convection, radiation and evaporation. In this situation, the mixed boundary condition at the initial time
That may be determined using boundary conditions associated with Equations (1.2), (1.3). For example, if the biological tissue is exposed to the environment then the transfer of heat between the skin surface and environment is due to conduction, convection, radiation and evaporation. In this situation, the mixed boundary condition at the initial time 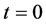 is given by
is given by
 (1.16)
(1.16)
where  denotes the body core temperature which is often regarded as a constant,
denotes the body core temperature which is often regarded as a constant, 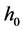 is the apparent heat convection coefficient between the skin surface and the surrounding medium under physiologically basal state and is an overall contribution from natural convection and radiation, and
is the apparent heat convection coefficient between the skin surface and the surrounding medium under physiologically basal state and is an overall contribution from natural convection and radiation, and 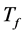 is the surrounding medium temperature (atmospheric temperature),
is the surrounding medium temperature (atmospheric temperature), 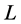 is the latent heat of evaporation, and
is the latent heat of evaporation, and 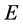 is the rate of sweat evaporation. Then inserting Equation (1.16) into solution (1.15) leads to the system that allows us to determine two of the three parameters
is the rate of sweat evaporation. Then inserting Equation (1.16) into solution (1.15) leads to the system that allows us to determine two of the three parameters ,
,  , and
, and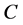 .
.
3. Results and Discussions
In the present section, we use the analytical solution (1.15) with sign “ ” to investigate the nonuniform temperature distribution inside the biological bodies. For numerical simulations, we use the tissue parameters shown in table 1 [3] [12] -[15] .
” to investigate the nonuniform temperature distribution inside the biological bodies. For numerical simulations, we use the tissue parameters shown in table 1 [3] [12] -[15] .
The maximal value of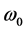 ,
,  , and
, and 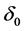 are
are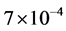 ,
, 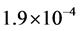 and
and , respectively [6] . The the arterial blood temperature
, respectively [6] . The the arterial blood temperature  is used. The distance between skin surface and the body core is taken to be
is used. The distance between skin surface and the body core is taken to be  [16] . The apparent heat convection coefficient due to natural convection and radiation is taken as
[16] . The apparent heat convection coefficient due to natural convection and radiation is taken as  while the surrounding fluid temperature is chosen as
while the surrounding fluid temperature is chosen as 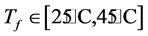 [17] , that is,
[17] , that is,
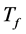 is comprised between 25˚C and 45˚C. For all our computations, we use
is comprised between 25˚C and 45˚C. For all our computations, we use  and
and 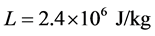 [13] [14] so that the effect of the sweat evaporation is neglected. It should be noted that the values for the metabolic level shown in table 1 are associated with dermal parts of the biological tissues.
[13] [14] so that the effect of the sweat evaporation is neglected. It should be noted that the values for the metabolic level shown in table 1 are associated with dermal parts of the biological tissues.
Using tissues’ properties given in table 1, the various temperature profiles have been studied. Figure 1 shows temperature-dependent perfusion distributions inside the four tissues with properties shown in table 1. To generate the plots of this figure, we have used a constant spatial heating with power 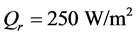 and the solution parameters
and the solution parameters 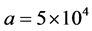 and Fat:
and Fat: ,
, 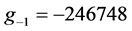 and
and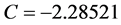 ; Kidney:
; Kidney: 

 and
and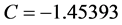 ; Bladder:
; Bladder: 

 and
and ; Tumor:
; Tumor: 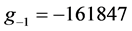

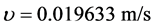 and
and . The plots of Figure 1 show that the tissue temperature increases with the thermal conductivity
. The plots of Figure 1 show that the tissue temperature increases with the thermal conductivity 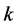 near the skin surface, and decreases near the body core when the thermal conductivity
near the skin surface, and decreases near the body core when the thermal conductivity  increases. Therefore, 1) the temperature of the fat tissue near the skin surface is lower than that of other tissues, and is higher near the body core than that of other tissues; 2) the temperature of the tumor tissue near the skin surface is higher than that of other tissues, and lower than that
increases. Therefore, 1) the temperature of the fat tissue near the skin surface is lower than that of other tissues, and is higher near the body core than that of other tissues; 2) the temperature of the tumor tissue near the skin surface is higher than that of other tissues, and lower than that

Table 1 . tissue parameters.
of other tissues near the body core.
In what follows, we concentrate ourselves to the temperature distribution in tumor tissue. Figure 2 gives the temperature profile in the tumor tissue under different kinds of surrounding medium characterized by their temperature. Obviously, the larger surrounding medium temperature, the higher temperature at the skin surface. Such information is valuable for thermal comfort evaluation. In practice, the values of the surrounding medium temperature and the duration of the process are to chosen so on considering that they should be in the safe range for the biological skin. Indeed, a long durable and high temperature of the surrounding medium will cause pain even burning to the skin tissues. The plots of figure 2 show that the temperature of each point of the tissue increases with time  (see plots (a), (b), and (c)). It is seen from plots (d) and (f) that near the skin surface, the temperature increases as a function of time
(see plots (a), (b), and (c)). It is seen from plots (d) and (f) that near the skin surface, the temperature increases as a function of time , while close to the body core, the temperature decreases with time
, while close to the body core, the temperature decreases with time . Far from the skin surface and from the body core, the temperature of the tissue at the early stage of heating process decreases, and then will gradually be improved (this is easily seen from plot (e)); moreover, as the time passes on, the temperature associated with the lower surrounding medium temperature increases more rapidly than that associated with higher temperature of the surrounding medium. In other words, a much longer time is needed to the tissue located far from the skin surface and the body core to reach the desired temperature when using a surrounding medium with higher temperature. It is also seen from plots (d) and (f) that the higher temperature of the tissue near the skin surface corresponds to the higher temperature of the surrounding medium; the situation is more different near the body core: surrounding medium with smallest temperature gives the highest temperature near the body core.
. Far from the skin surface and from the body core, the temperature of the tissue at the early stage of heating process decreases, and then will gradually be improved (this is easily seen from plot (e)); moreover, as the time passes on, the temperature associated with the lower surrounding medium temperature increases more rapidly than that associated with higher temperature of the surrounding medium. In other words, a much longer time is needed to the tissue located far from the skin surface and the body core to reach the desired temperature when using a surrounding medium with higher temperature. It is also seen from plots (d) and (f) that the higher temperature of the tissue near the skin surface corresponds to the higher temperature of the surrounding medium; the situation is more different near the body core: surrounding medium with smallest temperature gives the highest temperature near the body core.
Figure 3 and Figure 4 show the effect of parameters 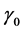 and
and  of the temperature-dependent blood
of the temperature-dependent blood
perfusion on the nonlinear temperature distribution in tumor tissue with properties given in table 1. The layer of air farthest from the skin was set at  and the core was set to
and the core was set to . Figure 3 shows the temporal distribution of temperature close to skin surface (Figure 3(a)) and close to the body core (Figure 3(b)) for different values of the linear coefficient of temperature dependence
. Figure 3 shows the temporal distribution of temperature close to skin surface (Figure 3(a)) and close to the body core (Figure 3(b)) for different values of the linear coefficient of temperature dependence . The two plots show that the tissue temperature decreases when parameter
. The two plots show that the tissue temperature decreases when parameter  of the temperature-dependent blood perfusion increases. Thus, the temperature of the tissue is lower if the blood perfusion has a higher linear coefficient of temperature dependence. Figure 4 shows the spatial distribution of temperature at different times. The plots of this figure show that the temperature of the tissue decreases when the quadratic coefficient
of the temperature-dependent blood perfusion increases. Thus, the temperature of the tissue is lower if the blood perfusion has a higher linear coefficient of temperature dependence. Figure 4 shows the spatial distribution of temperature at different times. The plots of this figure show that the temperature of the tissue decreases when the quadratic coefficient  of the temperaturedependent blood perfusion increases. As expected, Figure 3 and Figure 4 thus show that increased perfusion causes a decline in local temperature. As a consequence, the accumulated tissue damage will be lower if the blood perfusion has higher temperature coefficients. This means that one may manage the accumulated tissue damage just by manipulating parameters
of the temperaturedependent blood perfusion increases. As expected, Figure 3 and Figure 4 thus show that increased perfusion causes a decline in local temperature. As a consequence, the accumulated tissue damage will be lower if the blood perfusion has higher temperature coefficients. This means that one may manage the accumulated tissue damage just by manipulating parameters 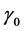 and
and  of the temperature-dependent blood perfusion.
of the temperature-dependent blood perfusion.
4. Conclusion
Using the extended mapping method with symbolic computation, we found exact analytical solution of the BHT equation with temperature-dependent blood perfusion, that describes the nonuniform temperature distribution in biological tissues. Using this solution, we have explicitly investigated temperature distribution in living tissues. The effects of the surrounding medium and the effects of the temperature-dependent blood perfusion on temperature distribution are also addressed. The exact solutions found in this work can be used to predicate the evolution of the detailed temperature within the tissues during thermal therapy.
Acknowledgements
This work was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) under grants Nos. 7033009.
NOTES
*Corresponding author.