Modified Tikhonov Method for Cauchy Problem of Elliptic Equation with Variable Coefficients

Hongwu Zhang

School of Mathematics and Information Science, Beifang University of Nationalities, Yinchuan, China.

DOI: 10.4236/ajcm.2014.43018                

Abstract

A Cauchy problem for the elliptic equation with variable coefficients is considered. This problem is severely ill-posed. Then, we need use the regularization techniques to overcome its ill-posedness and get a stable numerical solution. In this paper, we use a modified Tikhonov regularization method to treat it. Under the a-priori bound assumptions for the exact solution, the convergence estimates of this method are established. Numerical results show that our method works well.

Keywords

Ill-Posed Problem, Cauchy Problem, Elliptic Equation with Variable Coefficients, Tikhonov Regularization Method, Convergence Estimates

1. Introduction

In this paper, we consider the following Cauchy problem for the elliptic equation with variable coefficients in a strip region

(1)

where 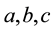are given functions such that for given positive constants,

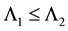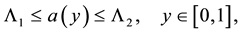(2)

(3)

Without loss of generality, in the following section we suppose that.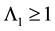

Let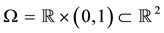, as in [1] , we assume that the unique solution of problem (1) exists in for the exact Cauchy data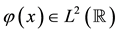. This problem is severely ill-posed and the regularization methods are required to stabilize numerical computations [2] [3] .

In 2007, Hào et al. [4] regularized problem (1) by adopting Poisson kernel to mollify the Cauchy data, and prove some condition stability estimates of Hlder and logarithm types for the solution and its derivatives. In 2008, Qian [5] used a wavelet regularization method to treat it. In 2010, [6] investigated the high dimension case for this problem, and constructed a stable regularization solution by using Gauss kernel to mollify Cauchy data. [7] treated this problem by a modified quasi-boundary value method in 2011. Following the above works, recently the reference [8] also solved problem (1) by using two iterative regularization methods, and obtained the convergence estimates of optimal order.

In this article, we continue to consider the problem (1). We adopt a modified Tikhonov regularization method to solve it. Under the a-priori bound assumptions for the exact solution, we give and proof the convergence estimates for this method. It can be seen that the convergence result is order optimal [9] -[11] as 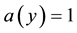for. In addition, for the Cauchy problem with non-homogeneous Dirichlet and Nuemann datum, it can be transformed into the above problem (1) by an auxiliary well-posed boundary problem. Hence, as in [1] [8] , here we only need to consider problem (1).

This paper is constructed as follows. In Section 2, we give some auxiliary results for this paper. In Section 3, we make the description for modified Tikhonov regularization method, and Section 4 is devoted to the convergence estimates for this method. Numerical results and some conclusions are shown in Sections 5-6, respectively.

2. Some Auxiliary Results

For a function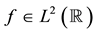, we define its Fourier transform as follow

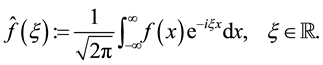(4)

Firstly, we consider the following Cauchy problem in the frequency domain

(5)

Lemma 2.1 [4] There exists a unique solution of (5) such that

(i),

(ii) is an entire function of for every,

(iii),

(iv) there exist positive constants, such that for

(6)

(7)

here, the definition of entire function can be found in [12] .

Secondly, Take the Fourier transform of problem (1) with respect to, then

(8)

It can be shown that, for, the solution of problem (1) in the frequency domain is

(9)

then, the exact solution of problem (1) can be expressed by

(10)

Note that, thus

(11)

Further, we suppose that there exists a constant, such that the following a-priori bounds exists

(12)

or

(13)

here denotes the Sobolev space -norm defined by

(14)

3. Modified Tikhonov Regularization Method

We firstly give the description for this method. Note that, from (9), we have

(15)

According to (15), for, we define the operator, then problem (1) can be expressed as the following operator equation

(16)

and

(17)

Let the exact and noisy datum satisfy

(18)

where denotes the -norm, the constant denotes a noise level.

Denote be the identical operator in, and be the adjoint operator for. In the ordinary Tikhonov regularization, we need solve the following minimum value problem

(19)

By Theorem 2.11 of Chapter 2 in [3] , the functional has a unique minimizer which is the unique solution of the following Euler equation

(20)

According to Parseval equality, we get

(21)

thus,

(22)

and

(23)

from (20), we have

(24)

Combing with (22), (23), (24), we can obtain that

(25)

hence,

(26)

using the inverse Fourier transform, we get the following Tikhonov regularization solution for problem (1)

(27)

Note that, the above Tikhonov regularization solution (27) can be interpreted as using the regularized kernel

to replace the kernel. Now, we replace the kernel with a much better regularized kernel, and obtain a modified Tikhonov regularization solution for problem (1)

(28)

4. Convergence Estimates

Now, we choose the regularization parameter by the a-priori rule and give the convergence estimates for this method.

Theorem 4.1 Suppose that given by (10) is the exact solution of problem (1) with the exact data and is the regularization solution defined by (28) with the measured data which satisfy (18), and the a priori bound (12) is satisfied. If we choose the regularization parameter, then for fixed, we have the following convergence estimate

(29)

where, ,.

Proof. From (10), (28), (18), (12), we have

(30)

According to Lemma 2.1, one can obtain that

(31)

Set, then

(32)

Let, we have

(33)

for, , it easily can be proven that the function has a unique maximum value point, such that

(34)

and note that,

(35)

thus, we get, i.e.,

(36)

From (34), we can derive that

(37)

combing with (36), (37), we have

(38)

Consequently,

(39)

Now we estimate. Note that,

(40)

adopting the similar proof procedure, we have

(41)

and

(42)

Hence,

(43)

From the selection of regularization parameter, (30), (39), (43), for the fixed, we can derive that

Theorem 4.1 shows that, for the fixed, the regularization solution defined by (28) is a stable approximation to the exact solution and the convergence result is the order optimal (Hölder type), but the estimate (29) gives no information about the error estimate at as the constraint (12) is too weak. For this purpose, as common, we can suppose that the stronger a-priori assumption (13) is satisfied.

Theorem 4.2 Suppose that given by (10) is the exact solution of problem (1) with the exact data and is the regularization solution defined by (28) with the measured data which satisfy (18), and the a priori bound (13) is satisfied. If we choose the regularization parameter, then at, we have the convergence estimate as follow

(44)

Proof. From (10), (28), (18), (13) and (14), we have

(45)

By Lemma 2.1, we can know

(46)

using the similar derivation processes with, in Theorem 4.1, we have

(47)

then from (45) and the selection rule, we get

(48)

Below, we estimate. From Lemma 2.1, we have

(49)

Case 1: for the large values with, we obtain

(50)

Case 2: for, one can get

(51)

Then, by (50), (51), we can obtain that

(52)

Consequently, from the selection rule, (45), (48), (52), we have

Remark 4.3 From the convergence estimate (44), we can see that the logarithmic term with respect to is

the dominating term. Asymptotically this yields a convergence rate of order, the first term is asymptotically negligible compared to this term.

5. Numerical Implementations

In this section, a numerical example is given to verify the stability and efficiency of our proposed method.

Taking, , then the solution of problem (5) can be expressed by, where. The exact data is taken as, the measured data is given by, where is the error level, the function returns an array of rsandom entries that is the same size as.

We use the discrete Fourier transform (DFT) and inverse Fourier transform (IFT) to complete our numerical experiments. The exact and regularized solutions are computed by (10) and (28), respectively. For, the numerical results at with (,) are shown in Figures 1(a)-(d), respectively. The regularization parameter is chosen by the description in Theorem 4.2.

In order to make a comprehensive analysis for the convergence with respect to the error level, we define the relative root mean square error (RRMSE) between the exact and approximate solutions as follow

(53)

and the corresponding computation results are shown in Table 1.

From Figures 1(a)-(d) and Table 1, we can see that the modified Tikhonov regularization method is stable and feasible, and as increases, the numerical becomes worse. Table 1 shows that the smaller is, the better the computed solution is, which is a common phenomenon in ill-posed Cauchy problem of elliptic equation.

6. Conclusion

A Cauchy problem for the elliptic equation with variable coefficients is considered. We use the modified Tikhonov regularization method to overcome its ill-posedness. Convergence estimates of this method are esta- blished under the a-priori selections for regularization parameter. Some numerical results show that our method works well.

Table 1., p = 3/4, the RRMSE for various noisy level.

Figure 1., , the exact and modified Tikhonov solutions.

Acknowledgements

The author would like to thank the reviewers for their constructive comments and valuable suggestions that improve the quality of our paper. The work described in this paper was supported by the NSF of China (11371181) and the SRF of Beifang University of Nationalities (2014XYZ08).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Regińska, T. and Regiński, K. (2006) Approximate Solution of a Cauchy Problem for the Helmholtz Equation. Inverse Problems, 22, 975-989. http://dx.doi.org/10.1088/0266-5611/22/3/015
[2]	Engle, H.W., Hanke, M. and Neubauer, A. (1996) Regularization of Inverse Problems. In: Mathematics and Its Applications, Vol. 375, Kluwer Academic Publishers Group, Dordrecht.
[3]	Kirsch, A. (1996) An Introduction to the Mathematical Theory of Inverse Problems. In: Applied Mathematical Sciences, Vol. 120, Springer-Verlag, New York.
[4]	Hào, D.N., Hien, P.M. and Sahli, H. (2007) Stability Results for a Cauchy Problem for an Elliptic Equation. Inverse Problems, 23, 421-461. http://dx.doi.org/10.1088/0266-5611/23/1/024
[5]	Qian, A.L. (2008) A New Wavelet Method for Solving an Ill-Posed Problem. Applied Mathematics and Computation, 203, 635-640. http://dx.doi.org/10.1016/j.amc.2008.05.009
[6]	Cheng, H., Feng, X.L. and Fu, C.L. (2010) A Mollification Regularization Method for the Cauchy Problem of an Elliptic Equation in a Multi-Dimensional Case. Inverse Problems in Science and Engineering, 18, 971-982. http://dx.doi.org/10.1080/17415977.2010.492519
[7]	Zhang, H.W. (2011) Modified Quasi-Boundary Value Method for Cauchy Problems of Elliptic Equations with Variable Coefficients. Electronic Journal of Differential Equations, 106, 1-10.
[8]	Zhang, H.W. and Wei, T. (2014) Two Iterative Methods for a Cauchy Problem of the Elliptic Equation with Variable Coefficients in a Strip Region. Numerical Algorithms, 65, 875-892. http://dx.doi.org/10.1007/s11075-013-9719-6
[9]	Fu, C.L., Li, H.F., Qian, Z. and Xiong, X.T. (2008) Fourier Regularization Method for Solving a Cauchy Problem for the Laplace Equation. Inverse Problems in Science and Engineering, 16, 159-169. http://dx.doi.org/10.1080/17415970701228246
[10]	Hohage, T. (2000) Regularization of Exponentially Ill-Posed Problems. Numerical Functional Analysis and Optimization, 21, 439-464. http://dx.doi.org/10.1080/01630560008816965
[11]	Tautenhahn, U. (1998) Optimality for Ill-Posed Problems under General Source Conditions. Numerical Functional Analysis and Optimization, 19, 377-398. http://dx.doi.org/10.1080/01630569808816834
[12]	Nikol’skii, S.M. (1975) Approximation of Functions of Several Variables and Imbedding Theorems. Springer, Berlin.