Plasma Internal Energy for Toroidal Elliptic Plasmas with Triangularity ()
1. Introduction
The linear treatment of the equilibrium equation in tokamaks was carried out by the Russians and result is the Grad-Shafranov equation [1,2]. The poloidal flux solution of the Grad-Shafranov equation determines the magnetic surface in the case when viscosity and nonlinear convective terms are neglected. In this case isobars and magnetic surface are coincidents [3,4]. However if the preceding terms are not neglected, it is not easy to find out a differential equation for the magnetic surface. In this paper, this problem has been treated and a differential equation for the magnetic surface has been found when vorticity is neglected. In the usual Grad-Shafranov equation the internal energy of the plasma does not appear, but in the present case internal energy appears as a quantity to be determined.
2. Extended Grad-Shafranov Equation
The time independent MHD momentum equation including viscosity and non-linear convective terms is [5]
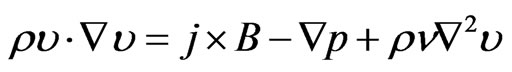 (1)
(1)
where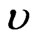 ,
, 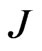 , and
, and 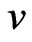 are the velocity, current density, and kinematic viscosity coefficient (assumed constant and isotropic), respectively. Here the anisotropic part of the pressure tensor is also neglected. Using the vorticity
are the velocity, current density, and kinematic viscosity coefficient (assumed constant and isotropic), respectively. Here the anisotropic part of the pressure tensor is also neglected. Using the vorticity 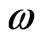
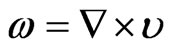 (2)
(2)
the first and last terms in Equation (1) can be written in a more convenient way as
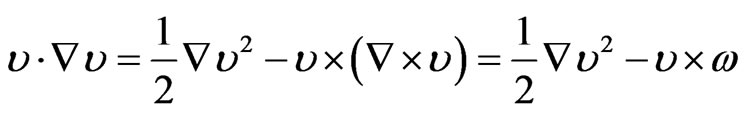 (3)
(3)
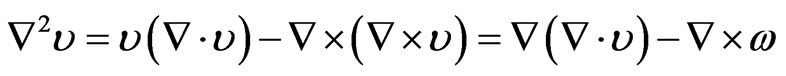 (4)
(4)
The temperature can also be assumed to be constant along a magnetic line [6], because of the high parallel thermal conduction. Thus the internal energy 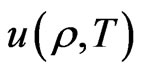 along the magnetic line will depend only on the density,
along the magnetic line will depend only on the density,
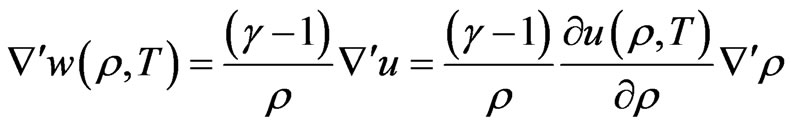
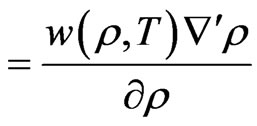 (5)
(5)
where 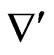 refers to a gradient in the plane of a magnetic surface, giving
refers to a gradient in the plane of a magnetic surface, giving
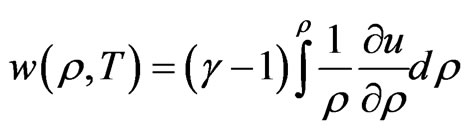 (6)
(6)
where the integral in Equation (6) is performed with T constant along a magnetic line [6] or in general on any line in the plane of a magnetic surface. The function 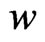 is actually the enthalpy of the plasma. This function
is actually the enthalpy of the plasma. This function  can be written explicitly using the entropy function
can be written explicitly using the entropy function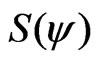 . The entropy is conserved in each magnetic surface [6] and the internal energy
. The entropy is conserved in each magnetic surface [6] and the internal energy 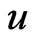 is given by
is given by
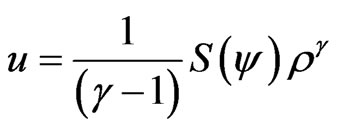 (7)
(7)
where  is the flux function and
is the flux function and 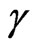 is 1 for an isotherm process or 5/3 for the adiabatic case [7]. Then
is 1 for an isotherm process or 5/3 for the adiabatic case [7]. Then 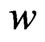 can be written as
can be written as
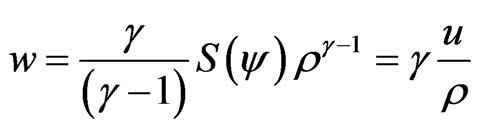 (8)
(8)
Now Equation (1) becomes
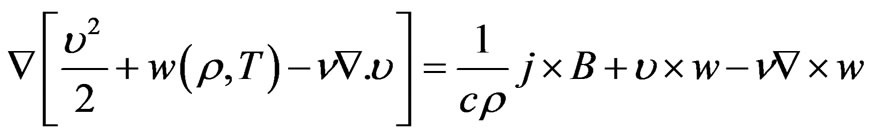 (9)
(9)
An auxiliary function 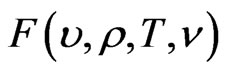 can be now be defined as
can be now be defined as
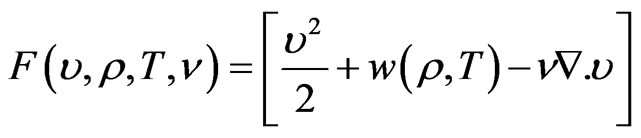 (10)
(10)
and the equilibrium equation will be written as
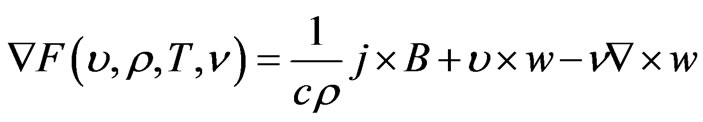 (11)
(11)
Considering now the low vorticity case, that is, 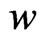 is a perturbation, then the low limit level will be with
is a perturbation, then the low limit level will be with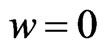 . Then the previous equation becomes,
. Then the previous equation becomes,
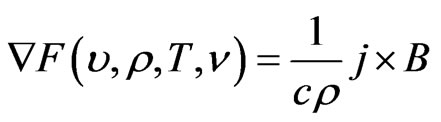 (12)
(12)
As in the linear case, the procedure to derive the GradShafranov equation can be followed obtaining an extended Grad-Shafranov equation
 (13)
(13)
where 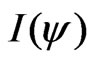 is the same kind of invariant as in the linear case and the operator
is the same kind of invariant as in the linear case and the operator  is
is
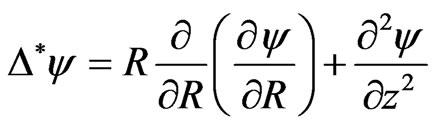 (14)
(14)
The internal energy in this extended Grad-Shafranov equation is a function of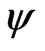 . Since F is only a function of
. Since F is only a function of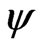 , and
, and 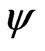 is function of
is function of 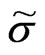 then Equation (12) can be written as
then Equation (12) can be written as
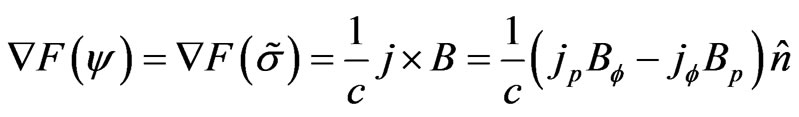 (15)
(15)
That is
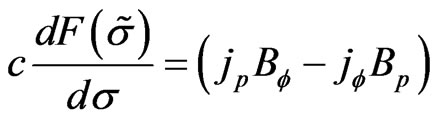 (16)
(16)
Since for the ideal MHD equilibrium confinement the internal energy and magnetic surfaces are coincident, then
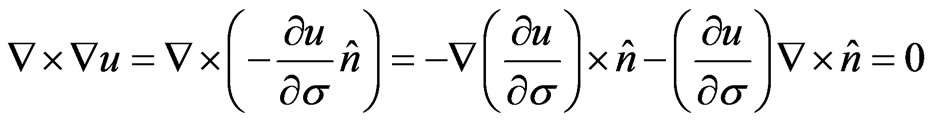 (17)
(17)
From [8], the operator
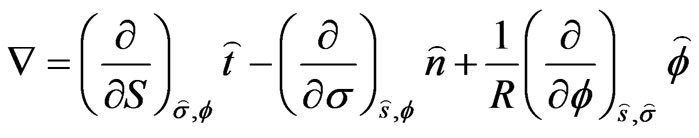
and because of the axissymmetry condition
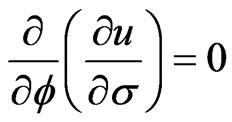 (18)
(18)
Similarly from [8], we also know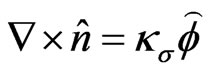 . Considering the
. Considering the 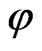 -component of Equation (17), the following differential equation is obtained:
-component of Equation (17), the following differential equation is obtained:
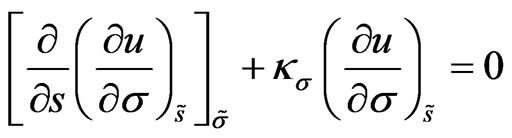 (19)
(19)
Then it leads to new surface invariant
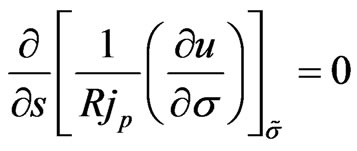 (20)
(20)
From the [9], we know
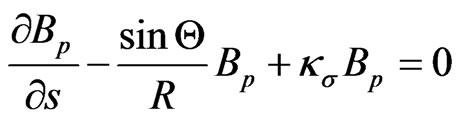 (21)
(21)
From the plasma pressure equilibrium equation [8], thus
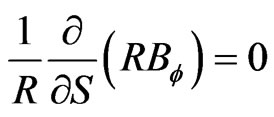 (22)
(22)
If we put together Equations (19), (21) , and (22) we obtain
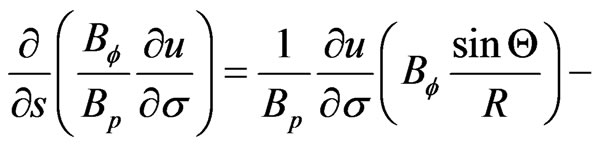
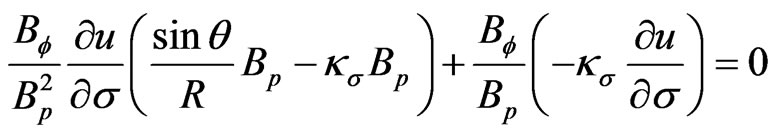 (23)
(23)
Experimental observations show that neutral beam injection and rf heating induces poloidal and toroidal plasma rotations in tokamaks. The analysis of plasma equilibrium performed by several authors [3-11] is much more complicated than those of plasma confinement with no rotation. The Grad–Shafranov equation has to be analyzed coupled with a Bernoulli-type equation and furthermore there are regions where that equation is of hyperbolic type instead of elliptic [5]. As it is well known, if nonlinear convective terms are included in the momentum equation, pressure is no longer a constant on the magnetic surfaces, but those terms cannot be neglected when significant poloidal or toroidal flows occur in tokamaks. However, as we show in this paper, if low vorticity can be assumed, important simplifications can be performed and some results can be obtained, which seem to be generalizations of those where convective terms were neglected. On the other hand this low vorticity approximation seems to be suitable for the H-mode in tokamaks, because of the characteristic low plasma turbulence induced by internal transport barriers [12-14]. Here a magnetohydrodynamics (MHD) treatment of plasma equilibrium is performed for low-vorticity plasmas including nonlinear convective terms and viscosity. Non-pressure-conserved functions have been found, which are characteristic of this kind of plasmas. Besides a partial differential equation (PDE) has also been derived for a function similar to the poloidal flux, which becomes the usual Grad–Shafranov (GS) equation, if the linear simplification is introduced. That kind of equation is referred here as an extended GS equation.
3. Conclusions
A simplified equilibrium analysis in tokamak has been performed for the nonlinear momentum equation with viscosity in the low vorticity case. Internal energy is not constant now on magnetic surfaces, but our analysis shows that other significant magnetic surface new invariant appears, which are useful to determine equilibrium conditions. An extended Grad-Shafranov (GS) -type equation has been derived in this case. This new equation includes the usual invariant 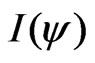 depending on the toroidal magnetic field plus some additional functions such as Internal energy. This extended GS equation is a PDE elliptic type, which could be a little more laborious to calculate than the usual GS equation.
depending on the toroidal magnetic field plus some additional functions such as Internal energy. This extended GS equation is a PDE elliptic type, which could be a little more laborious to calculate than the usual GS equation.