Derivation of Multipurpose Single Reservoir Release Policies with Fuzzy Constraints ()
1. Introduction
Uncertainty modeling may contribute to better reservoir management. Recent research in modeling uncertainty in water resources systems has highlighted the use of fuzzy logic based approaches. A variety of optimization model has been developed so far to facilitate the real-time operations of the reservoir systems, a summary can be found in Yeh [1]. Labadie [2] has given state-of-the-art review on optimal operation of multireservoir systems. The purpose of this review is to assess the state-of-the-art in optimization of reservoir system management operations and consider future directions for additional research and applications. In many practical situations, it is not reasonable to require that the constraints or the objective function in linear programming problems be specified in precise, crisp terms. In such situations, it is desirable to use some type of FLP [3]. Loucks et al. [4] has given development and application of quantitative mathematical modelling methods to problems of water management. FLP is not a uniquely defined type of model but that many variations are possible, depending on the assumptions or features of the real situations to be modeled [5]. Mohan and Jothiprakash [6] have developed a model for optimal crop planning where fuzziness is involved in the input variables such as inflows and ground water pumpage are considered in the FLP model. Gasimov and Yenilmez [7] have explained the methodology for solving FLP problem by using linear membership function with numerical examples. A FLP problem has been solved without using any ranking function. Fontane et al. [8] addresses the imprecise and noncommensurable objectives for planning reservoir operation by using fuzzy membership functions, and explored the utility of the approach in dynamic programming. Jairaj and Vedula [9] applied fuzzy set theory in a linear programming model for multireservoir systems where the uncertainty in reservoir inflows has been considered by treating them as fuzzy sets. Kindler [10] used fuzzy set theory to develop a water allocation model assuming water requirement as a fuzzy quantities. Rommelfanger [11] presented a review of methods for solving fuzzy linear programs. Various methods of parameter fuzzification were discussed i.e. LP models with soft constraints and LP models with fuzzy coefficients of constraints and/or of the objective function may be fuzzy are outlined. In the real world most of the parameters used are very uncertain. Therefore even if the linear programming simplification is accepted, neither the constraints nor the expected revenue can be characterized by certainty. Therefore fuzzy set representations of the unit revenue of each use together with a fuzzy representation of each set of constraints are used to expand the capabilities of the linear programming formulation [12]. Anand Raj and Nagesh Kumar [13,14] introduced new method of fuzzy ranking with the concept of maximizing set and minimizing set. The method of RANking FUzzy Weights (RANFUW) is computationally simple and easy to implement. The proposed method was applied (RANFUW method) to a river basin planning and management problem. The method practiced on the Krishna River basin to find the most suitable planning of the reservoirs with their associated purposes. A multiobjective linear programming (MOLP) with fuzzynumbered cost coefficients is discussed by Wang and Wang [15]. Based on membership function, problem is transformed into a multiobjective problem with parametrically interval-valued MOLP problem. Srinivasa Raju and Nagesh Kumar [16] have developed FLP irrigation planning model for the evaluation of management strategies for the case study of Sri Ram Sager Project, Andhra Pradesh, India. The study has demonstrated that how vagueness and imprecision in the objective function values can be quantified by membership function in a fuzzy multiobjective framework. Regulwar and Anand Raj [17] developed 3-D optimal surface for operation policies of a multireservoir in a fuzzy environment using Genetic Algorithm (GA) for river basin development and management. A multi objective multireservoir operation model for maximization of irrigation releases and maximization of hydropower production is proposed using GA. Theseobjectives are fuzzified and are simultaneously maximized by defining and then maximizing level of satisfaction (λ).
A monthly operating rule for single reservoir operation is developed by Kim et al. [18]. Synthetic inflow data over 100 years are generated by using a time series model, AR(1), and piecewise-linear operating rules consisting of 4 and 5 linear lines are found using the implicit stochastic optimization method. In order to consider multiobjective functions in reservoir system operation, a multiobjective genetic algorithm (NSGA-II) is adopted to obtain the optimization results. Sahinidis [19] has given state-of-the-art and opportunities on optimization under uncertainty. The study reviews theory and methodology that have been developed to cope with the complexity of optimization problems under uncertainty. Finally, he has discussed the several main areas for future development in this field. The fuzzy rule based systems are very much suitable for inferring developed operating policies. Uncertainty modeling may contribute to better reservoir management by identifying and quantifying the sources of significant uncertainty in predicting reservoir and river conditions that affect environmental habitats and recreational conditions. Carron et al. [20] modeled uncertainty in an object oriented reservoir operation model. The methodology is applied to a case study from the lower Colorado River, where a preexisting deterministic model is used for reservoir operation and planning. The case study involves evaluation of uncertainties associated with prescribed reservoir pool elevations for purposes of recovering endangered fish species. Deka and Chandramouli [21] studied fuzzy neural network modeling of reservoir operation. Study aims at the application of the hybrid model, which consist of artificial neural network and fuzzy logic in reservoir operating policy during critical period. The proposed hybrid model i.e. Fuzzy Neural Network (FNN) combines the learning ability of artificial neural networks and the transparent nature of fuzzy logic. Regulwar and Anand Raj [22] have studied multiobjective multireservoir optimization in fuzzy environment for river basin development and management. A model is proposed using GA under fuzzy environment. The optimal operation policy obtained by the model is compared with the actual average operation policy for Jayakwadi reservoir stage–I. Mujumdar [23] gave a brief over view of some mathematical tools for irrigation system operation, crop water allocations and performance evaluation. Esogbue and Liu [24] proposed the treatment of complex reservoir operation problems via newly developed tool of fuzzy criterion decision process. This new approach has been shown to be more flexible and useful analysis tool especially when it is desirable to incorporate an expert’s knowledge into the decision models. A fuzzy rule based model is developed by Panigrahi and Mujumdar [25] for operation of single purpose reservoir. The model operates on an “if-then” principle where ‘if’ is a vector of fuzzy premises and the ‘then’ is a vector of fuzzy consequences. Savic and Simonovic [26] used fuzzy set method to model for a chance constrained reservoir operation for selecting risk levels. Shrestha et al. [27] proposed the input to the reservoir operating principles (e.g. initial storage, inflows, and demands), as well as outputs (historical releases) could be described by fuzzy relations. These fuzzy inputs are combined to produce fuzzy output relation, which can be combined and defuzzified to get crisp output.
From the literature review, it is observed that number of research contributions exist in the literature that deals with uncertainty in water resources systems including fuzziness, subjectivity, imprecision and lack of adequate data. However, it is observed that most of the literature considers fuzziness/uncertainty with very few parameters and/or in objectives [6,10,12,16,17,22,25] of the reservoir operation model. To integrate all uncertainties, the application of fuzzy set theory to water resources system is illustrated in present study through the formulation of a fuzzy linear programming model to a multipurpose single reservoir. The major features of this study distinguish it from the earlier research which address the problem of reservoir operation: its capability to consider the uncertainty in all parameters (such as reservoir storages, releases for irrigation, and releases for hydropower production, irrigation demands, and power demands). Here the technological coefficients as well as resources of the linear programming model are considered as a fuzzy in nature. Initially in model I, results have been obtained by solving model I for fuzzy resources. Next model II is solved for fuzzy technological coefficients. Finally model III is solved by simultaneously considering fuzzy resources and fuzzy technological coefficients. The methodology is illustrated through a case study of Jayakwadi reservoir stage-II built across river Sindaphana, Maharashtra State, India.
2. Methodology
Water resources systems have to be planned by considering uncertain inputs due to fluctuating demands, increase in population, basin development, water usage, human activities and other technological development. This uncertainty is inevitable in the reservoir operation model due to lack of the perfect understanding of the phenomenon and process involved in addition to the random nature of the events. Some of the sources of the uncertainties related to the reservoir operation can be summarized as: spatial variation may be inconsistent or not representative, modeling inaccuracy: parameter assumptions, randomness of natural phenomena, climate change, extreme events, operational variability, future socio-economics objectives, maintenance. Reservoir storages are uncertain due to variation in inflows and some time vague due to poor operation. Stochastic crop net irrigation requirement (NIR) contributes uncertainty in irrigation demands. NIR is influenced by temperature, precipitation and the rate of crop development. Further irrigation demands, although driven by weather conditions to a large extent, are also impacted by crop type, market conditions, period of planting and harvest. Release and storage targets for a reservoir operation are usually decided based on factors defining the functional requirement of the reservoir systems. These include, for example, downstream water demand; flood control requirement; expected damage; political and social impacts of reservoir operation. The decision maker considers all these issues, and applies personal judgment to decide on the target value, and thus the target becomes practically subjective in nature. Uncertainty also occurs from imprecise knowledge of current or future demands placed on the system. For example, reservoirs that are used to generate peaking hydroelectric power are subject to the whims of electricity pricing, consumer demand. Uncertainty is involved in objectives in the sense that the values and targets are usually subjective, and the relative emphases on different objectives change with time. In many cases, fuzzy logic may provide the most appropriate methodological tool for modeling reservoir operation. In this study, the applicability of the reservoir operation model is improved by incorporating the uncertainties in model parameters and representing those as fuzzy sets instead of single values. The degree of satisfaction  of a certain value of the parameter within the fuzzy set is represented by a membership function. In present study while modeling of reservoir operation with fuzzy logic, the following steps are followed, i.e. fuzzification of inputs, where the crisp parameters such as reservoir storages, releases, irrigation demands, power demands and storages of the reservoir are transformed into fuzzy parameters. In present section, three FLP models are presented which considers uncertainty in various parameters gradually. In model I, the technological coefficients are taken as a crisp numbers while the resources are characterized by uncertainties. In model II, the technological coefficients are fuzzy numbers and resources are crisp in nature. In model III, FLP formulation considers both technological coefficients and resources are characterized by uncertainty. In this section, formulation of these three FLP models is explained.
of a certain value of the parameter within the fuzzy set is represented by a membership function. In present study while modeling of reservoir operation with fuzzy logic, the following steps are followed, i.e. fuzzification of inputs, where the crisp parameters such as reservoir storages, releases, irrigation demands, power demands and storages of the reservoir are transformed into fuzzy parameters. In present section, three FLP models are presented which considers uncertainty in various parameters gradually. In model I, the technological coefficients are taken as a crisp numbers while the resources are characterized by uncertainties. In model II, the technological coefficients are fuzzy numbers and resources are crisp in nature. In model III, FLP formulation considers both technological coefficients and resources are characterized by uncertainty. In this section, formulation of these three FLP models is explained.
Model I: The fuzzy linear programming problem with fuzzy resources
 (1)
(1)
In this case,  is a fuzzy numbers with the following linear membership function
is a fuzzy numbers with the following linear membership function
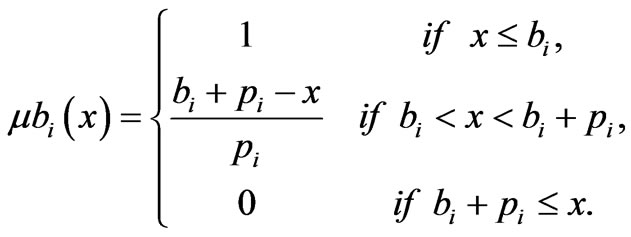 (2)
(2)
where  (Figure 2). For each vector
(Figure 2). For each vector , we first calculate the degree,
, we first calculate the degree,  to which
to which  satisfies the
satisfies the  constraint
constraint  by the formula
by the formula
 (3)
(3)
These degrees are fuzzy set on , and their intersection,
, and their intersection,  is a fuzzy feasible set. Next, to determine the fuzzy set of optimal values. This is done by calculating the lower and upper bounds of the optimal values first. The lower bound of optimal values
is a fuzzy feasible set. Next, to determine the fuzzy set of optimal values. This is done by calculating the lower and upper bounds of the optimal values first. The lower bound of optimal values  is obtained by solving the standard linear programming problem;
is obtained by solving the standard linear programming problem;
 (4)
(4)
The upper bound of the optimal values,  is obtained by a similar linear programming problem in which each
is obtained by a similar linear programming problem in which each  is replaced with
is replaced with :
:
 (5)
(5)
Then the fuzzy set of optimal values,  which is fuzzy subset of
which is fuzzy subset of  is defined by a linear membership function
is defined by a linear membership function  for objective as,
for objective as,
 (6)
(6)
Graphical representation of linear membership function given by Equation (6) for fuzzy goals is shown in Figure 1.
The fuzzy set of the 
 constraint,
constraint,  which is subset of
which is subset of , is defined by
, is defined by
 (7)
(7)
Graphical representation of linear membership function given by Equation (7) for fuzzy resources is shown in Figure 2.
By incorporating the above information, the problem given by Equation (1) becomes the following optimization problem
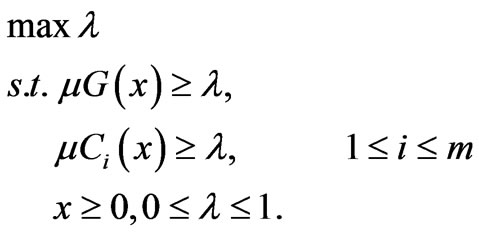 (8)
(8)

Figure 1. Linear membership function for goals.

Figure 2. Linear membership function for resources .
.
By using Equations (6), (7), Equation (8) can be written as
 (9)
(9)
where,  is the level of satisfaction. The above problem is actually a problem of finding
is the level of satisfaction. The above problem is actually a problem of finding  such that
such that
 (10)
(10)
reaches the maximum value; that is a problem of finding a point  which satisfies the constraints and goal with the maximum degree. The method employed here is called as symmetric method (i.e. the constraints and the goal are treated symmetrically).
which satisfies the constraints and goal with the maximum degree. The method employed here is called as symmetric method (i.e. the constraints and the goal are treated symmetrically).
Model II: Fuzzy linear programming problem with fuzzy technological coefficients
 (11)
(11)
 is a fuzzy number with the following linear membership function:
is a fuzzy number with the following linear membership function:
 (12)
(12)
where  and
and . For defuzzification of this problem, we first fuzzify the objective function. This is done by calculating lower and upper bounds of the optimal values first. The bounds of the optimal values
. For defuzzification of this problem, we first fuzzify the objective function. This is done by calculating lower and upper bounds of the optimal values first. The bounds of the optimal values  and
and  are obtained by solving the standard linear programming problem.
are obtained by solving the standard linear programming problem.
 (13)
(13)
and
 (14)
(14)
The objective function takes values between  and
and  while technological coefficient vary between
while technological coefficient vary between  and
and . Let
. Let  = min
= min 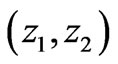 and
and  = max
= max . Then,
. Then,  and
and  are called the lower and upper bounds of the optimal values, respectively.
are called the lower and upper bounds of the optimal values, respectively.
Linear crisp problems have finite optimal values. In this case the fuzzy set of optimal values,  , which is subset of
, which is subset of , is defined as
, is defined as
 (15)
(15)
The fuzzy set of the 
 constraint,
constraint, 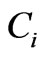 which is subset of
which is subset of , is defined by Equation (16).
, is defined by Equation (16).
 (16)
(16)
The linear membership function used for fuzzy goals is same as shown in Figure 1. The linear membership function used for fuzzy technological coefficients ( ) given by Equation (16) is shown graphically in Figure 3.
) given by Equation (16) is shown graphically in Figure 3.
Using above linear membership functions, LP problem given by Equation (11) becomes following optimization problem.
 (17)
(17)

Figure 3. Linear membership function for fuzzy technological coefficients .
.
 (18)
(18)
By using Equations (15), (16), the problem (17) can be written as
 (19)
(19)
Model III: Fuzzy linear programming problem with fuzzy technological coefficients and fuzzy resources
In the following problem FLP model with fuzzy technological coefficients and fuzzy right-hand-side numbers have presented.
 (20)
(20)
 and
and  are fuzzy numbers with the following linear membership function:
are fuzzy numbers with the following linear membership function:
 (21)
(21)
and
 (22)
(22)
where . For defuzzification of the problem, we first calculate the lower and upper bounds of the optimal values. The optimal values
. For defuzzification of the problem, we first calculate the lower and upper bounds of the optimal values. The optimal values  and
and  can be defined by solving the following linear programming problems,
can be defined by solving the following linear programming problems,
 (23)
(23)
 (24)
(24)
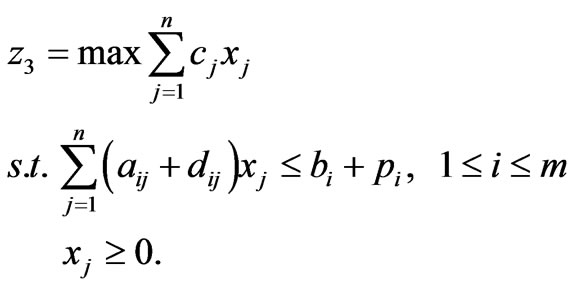 (25)
(25)
and
 (26)
(26)
Let . The objective function takes values between
. The objective function takes values between  and
and  while technological coefficients takes values between
while technological coefficients takes values between 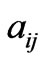 and
and  and the resources takes values between
and the resources takes values between  and
and .
.
Then the fuzzy sets of the optimal values,  , which is subset of
, which is subset of , is defined by
, is defined by
 (27)
(27)
The fuzzy set of ith constraint,  which is subset of
which is subset of  is defined by Equation (27).
is defined by Equation (27).
The above linear membership function for both fuzzy technological coefficients  and fuzzy resources
and fuzzy resources  given by Equation (27) is represented graphically in Figure 4. The linear membership function used for fuzzy goals is same as shown in Figure 1.
given by Equation (27) is represented graphically in Figure 4. The linear membership function used for fuzzy goals is same as shown in Figure 1.
Then, by using the method of defuzzification, as for the problem (17), the problem given by Equation (19) is reduced to following crisp problem:
 (28)
(28)
A reservoir operation model is developed by using above FLP formulation and applied to the case study of Jayakwadi reservoir stage-II. Results have been obtained for fuzzy resources, fuzzy technological coefficients and by considering both; fuzzy resources and fuzzy technological coefficients.
3. Case Study
The physical system is considered the Jayakwadi reservoir stage-II, a multipurpose project, created by constructing a dam across the river Sindaphana, a tributary of river Godavari, in Aurangabad district, Maharashtra State, India as shown in Figure 5. The gross storage of reservoir is 453.64 Mm3 and live storage is 313.30 Mm3. The total installed capacity for power generation is 2.25MW. Irrigable command area is 938.85 km2.
The 75% dependable monthly inflows into the reservoir are shown in Table 1. Monthly irrigation demands were determined with the help of crop calendar, water requirements for various crops during different growth stages and the types of soils. Monthly irrigation demands in a water year are also shown in Table 1.
4. Formulation of FLP Model
Following generalized LP model is developed for

Figure 4. Linear membership function for both fuzzy technological coefficients ( ) and fuzzy resources (
) and fuzzy resources ( ).
).
monthly operation of the reservoir assuming stationary inflows in a water year. As explained in methodology, FLP formulations are incorporated in following generalized linear programming model.
4.1. Objective Function
The two objectives are considered in the model are:
1) Maximization of releases for irrigation (i.e., RI).

Table 1. Monthly inflows and irrigation demands for Jayakwadi reservoir stage–II.
 (29)
(29)

Figure 5. Location of jayakwadi reservoir stage-II.
2) Maximization of releases for hydropower production (i.e., RP).
 (30)
(30)
where TOTRI is the total releases for irrigation in all the time periods and TOTRP is the total releases for hydropower production. These objective functions can be written as,
 (31)
(31)
4.2. Constraints
Turbine release constraint Release for the turbine for hydropower production should be less than or equal to turbine capacity (TC) in each month (t), and it should be greater than or equal to the firm release committed for that month.
 (32)
(32)
Irrigation demand constraint Release into canals for irrigation (RI) should be less than or equal to maximum irrigation demand (ID). Release should also be greater than minimum releases required for irrigation so that crop will not wilt. In the present case 30% of the maximum irrigation demand is considered as minimum irrigation demand for all the time periods.
 (33)
(33)
Reservoir storage capacity constraint The live storage in the reservoir should be less than or equal to the maximum capacity (SC) and greater than or equal to minimum storage capacity  for all the time periods.
for all the time periods.
 (34)
(34)
Reservoir storage continuity constraint These constraint relate to the releases for the turbine (RP)t, releases for irrigation (RI)t, reservoir storage (S)t, inflow(I)t into the reservoir, feeder canal release (FCR)t, overflows (OVF)t and the evaporation losses (L)t for all the time periods. Here evaporation losses are considered as a function of storage and by assuming a linear relationship between reservoir water surface area and storage. The storage continuity constraint can be written as follows.
 (35)
(35)
where
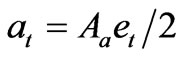
 is surface area of the reservoir per unit active storage volume.
is surface area of the reservoir per unit active storage volume.
 is surface area of the reservoir corresponding to the dead storage volume.
is surface area of the reservoir corresponding to the dead storage volume.
 is evaporation rate for month t in depths units.
is evaporation rate for month t in depths units.
The fuzzy linear programming model is formulated in this section is applied to the case study, and is solved using LINGO (Language for Interactive General Optimization).
5. Results and Discussions
In this study three models of FLP are considered and they are applied to the Jayakwadi reservoir stage–II. The two objectives are considered in all the model viz. maximization of releases for irrigation (RI) and maximization of releases for hydropower production (RP). As explained in methodology, initially the model considers uncertainty involved in resources  i.e. irrigation demands, power demands and maximum storage in any time period t in the reservoir are considered as fuzzy resources while technological coefficients are considered crisp in nature. By adopting the methodology explained, using Equations (4,5) the lower bound Zl and upper bound Zu for both the objectives (Viz, Z1: Releases for Irrigation and Z2: Releases for Hydropower) are determined by considering one objective at a time. These values are given in Table 2. When Z1 is maximized, the corresponding value of Z2 considered being worst and vice versa.
i.e. irrigation demands, power demands and maximum storage in any time period t in the reservoir are considered as fuzzy resources while technological coefficients are considered crisp in nature. By adopting the methodology explained, using Equations (4,5) the lower bound Zl and upper bound Zu for both the objectives (Viz, Z1: Releases for Irrigation and Z2: Releases for Hydropower) are determined by considering one objective at a time. These values are given in Table 2. When Z1 is maximized, the corresponding value of Z2 considered being worst and vice versa.
By determining the lower and upper bound of objective functions, a linear membership function given by Equation (6) has been used to fuzzify the objectives and Equation (7) has been used for fuzzy resources. By incorporating above information in Equation (9) model is solved for maximization of level of satisfaction  which satisfied the constraints and goal with the maximum degree. Results for maximized
which satisfied the constraints and goal with the maximum degree. Results for maximized  for fuzzy resources are given in Table 3. Next, the FLP model is solved for fuzzy technological coefficients
for fuzzy resources are given in Table 3. Next, the FLP model is solved for fuzzy technological coefficients  i.e. releases for irrigation (RI), releases for hydropower production (RP) and storages in the reservoir (S) in any time period t are considered fuzzy in nature while resources have been considered crisp in nature. In this model using the Equations (13) and (14), lower bound (Zl) and upper bound (Zu) for both the objectives are determined by considering one objective at a time as calculated for fuzzy resources. When Z1 is maximized, the corresponding value of Z2 considered being worst and vice versa. By determining the bounds for objectives, a linear membership function has been formed for objectives and constraints using Equations (15) and (16). Finally a model is solved for maximization of satisfaction level
i.e. releases for irrigation (RI), releases for hydropower production (RP) and storages in the reservoir (S) in any time period t are considered fuzzy in nature while resources have been considered crisp in nature. In this model using the Equations (13) and (14), lower bound (Zl) and upper bound (Zu) for both the objectives are determined by considering one objective at a time as calculated for fuzzy resources. When Z1 is maximized, the corresponding value of Z2 considered being worst and vice versa. By determining the bounds for objectives, a linear membership function has been formed for objectives and constraints using Equations (15) and (16). Finally a model is solved for maximization of satisfaction level  using Equation (18). The results for maximized
using Equation (18). The results for maximized 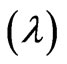 for fuzzy model II are presented in Table 3. Finally model III is solved by considering both fuzzy i.e. fuzzy resources and fuzzy technological coefficients. In this model, the lower bound (Zl) and upper bound (Zu) for objectives are calculated from the values obtained by solving Equations (22 to 25). By using the Equations (26) and (27) a linear membership functions are formed for objectives and constraints and then by using Equation (28) model is solved for maximization of
for fuzzy model II are presented in Table 3. Finally model III is solved by considering both fuzzy i.e. fuzzy resources and fuzzy technological coefficients. In this model, the lower bound (Zl) and upper bound (Zu) for objectives are calculated from the values obtained by solving Equations (22 to 25). By using the Equations (26) and (27) a linear membership functions are formed for objectives and constraints and then by using Equation (28) model is solved for maximization of . Results so obtained are given in Table 3.
. Results so obtained are given in Table 3.
Optimal operating policies have been given in Table 3 for three models of fuzzy linear programming as explained in the section of methodology. For model I, annual releases obtained for irrigation are 347.84 Mm3 and releases for hydropower are 233.56 Mm3 and level of satisfaction  is 0.53. Similarly when the uncertainty considered in technological coefficients of the model, annual releases obtained for irrigation are 347.43 Mm3 and releases for hydropower are 233.17 Mm3 and level of satisfaction
is 0.53. Similarly when the uncertainty considered in technological coefficients of the model, annual releases obtained for irrigation are 347.43 Mm3 and releases for hydropower are 233.17 Mm3 and level of satisfaction  is 0.528. Similarly when the uncertainty considered in both fuzzy resources and fuzzy technological coefficients, the annual releases obtained for irrigation are 346.47 Mm3 and releases for hydropower are 232.31 Mm3 and level of satisfaction is
is 0.528. Similarly when the uncertainty considered in both fuzzy resources and fuzzy technological coefficients, the annual releases obtained for irrigation are 346.47 Mm3 and releases for hydropower are 232.31 Mm3 and level of satisfaction is  0.525. From above results it can be observed that there is average 1 Mm3 difference between annual releases obtained by first two models and in model III.
0.525. From above results it can be observed that there is average 1 Mm3 difference between annual releases obtained by first two models and in model III.
Also by model III, in the month of June, February, March, April and May the releases for irrigation are 2.316 Mm3, 9.006 Mm3, 8.694 Mm3, 10.67 Mm3 and 7.764 Mm3 respectively. Same releases for irrigation have been obtained by model I and model II. For these particular months all the FLP model has satisfied minimum irrigation requirements. The result of the third model shows that the releases for irrigation and hydropower are uniformly distributed over time period. It can be observed that in first two models, in the month of August, September and October, the releases for irrigation and hydropower are more than the releases obtained by third

Table 2. Upper and Lower bounds of the objective function for .
.


Table 3. Release policy for fuzzy resources, fuzzy technological coefficients and both fuzzy resources, fuzzy technological coefficients.
model. But in first model, the technological coefficients are considered crisp in nature and in model II, the resources are considered crisp in nature. In real world situations, it is not feasible to presume that uncertainty is involved either only in technological coefficients or resources. The model III has considered uncertainty comprehensively in all the parameters of reservoir operation model by considering fuzzy resources (i.e. irrigation demands, power demands and maximum storage) and fuzzy technological coefficients (i.e. release for irrigation, release for power and storages in reservoir in any time period t). By considering this situation it can be observed that the optimal operating policy obtained by considering fuzziness involved in resources and technological coefficients gives more realistic results. Results obtained by model III are slightly deviated from results obtained by first two models. Therefore, it is appropriate to consider the uncertainty, fuzziness in resources and technological coefficients in the reservoir operation model rather than considering one of them as a crisp in nature. Release policy obtained by all the three cases for irrigation and
hydropower have been shown graphically in Figures 6, 7. Figure 8 represent the hydropower produced in KWH for three cases in a water year.
6. Conclusions
Most of the water resources system models, setting up goals, limits on constraints, standards for non-violation and even objective functions introduce uncertainty due to subjectivity and imprecision. Recent interest in addressing uncertainty in water resources systems is due not only randomness but also to imprecision, subjectivity and human judgment, and lack of data/information has led the use of fuzzy system theory. Present study demon
strates a methodology for addressing uncertainty in demands, storages and releases within a linear modeling framework. The technique is useful alternative for reservoir operation models that contain more than few imprecise parameters in constraints.
The modeling procedure demonstrated that how vagueness/uncertainty in various parameter of reservoir operation model can be incorporated gradually in resources, in technological coefficients of the model along with imprecise objectives. The advantage of fuzzy logic model is that the calculations are straight forward and the model is easy for the operator to understand due to its structure. The adoption of a particular model with the associated coefficients of the optimization model is on the decision maker to suit his preferences structure and the values associated with various issues related to the problem. However comparison of the various parameter fuzzification and results indicates that model III is quite versatile and can be used in all situations where all the parameters of reservoir operation are not well defined. This is due to reason that in real world situation; it is not feasible to presume that uncertainty is involved either only in resources or in releases and storages. Overall satisfaction level 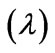 achieved by all the three models is in the range of 0.53 but it depends on the operation manager to understand the sensitivity of the optimal solution and his decision to consider uncertainty in the model based on situation in operation time period.
achieved by all the three models is in the range of 0.53 but it depends on the operation manager to understand the sensitivity of the optimal solution and his decision to consider uncertainty in the model based on situation in operation time period.
7. Acknowledgements
The authors are thankful to Command Area Development Authority, Aurangabad, Maharashtra State, India for providing necessary data for the analysis.
Nomenclatures
FRt: Firm release during month t.
IDt: Maximum Irrigation demand during month t.
IDMint: Minimum irrigation demand during month t.
It: Inflows into the reservoir during month t.
RIt: The releases into canals for irrigation during month t RPt: The releases for hydropower production during month t.
RWSt: Release for water supply during month t.
SCt: The storage capacity of the reservoir during month t.
St: The storage in the reservoir during month t.
SMint: Minimum storage capacity during month t.
TC: Flow through turbine capacity OVFt: Overflow from the reservoir during month t.
λ: Level of satisfaction.
 : Fuzzy technological coefficients
: Fuzzy technological coefficients
 : Fuzzy resources
: Fuzzy resources