Effects of Thermal Diffusion and Chemical Reaction on MHD Flow of Dusty Visco-Elastic (Walter’s Liquid Model-B) Fluid ()
1. Introduction
Many transport processes exist in nature and industrial application in which the transfer of heat and mass occurs simultaneously as a result of combined buoyancy effects of thermal diffusion and diffusion of chemical species. In the last few decades several efforts have been made to solve the problems on heat and mass transfer in view of their application to astrophysics, geophysics and engineering.
Chemical reaction can be codified either heterogeneous or homogeneous processes. Its effect depends on the nature of the reaction whether the reaction is heterogeneous or homogeneous. A reaction is of order n, if the reaction rate is proportional to the nth power of concentration. In particular, a reaction is of first order, if the rate of reaction is directly proportional to concentration itself. Experimental and theoretical works on MHD flow with thermal diffusion and chemical reaction have been done extensively in various areas i.e. sustain plasma confinement for controlled thermo nuclear fusion, liquid metal cooling of nuclear reactions and electromagnetic casting of metals. Chambre and Yang [1] have worked on thermal diffusion of a chemically reactive species in a laminar boundary layer flow. Dusty viscous and visco-elastic fluids have been discussed by Saffman [2], Micheal and Norey [3], Raptis and Perdikis [4]. Singh [5] proposed the study of free convection and mass diffusion of a dusty visco-elastic (Walter’s Liquid Model-B) fluid flowing between two heated porous plates in porous media in presence of magnetic field. References [6,7] focused on the study of convective heat and mass transfer incompressible, viscous Boussinesq fluid in presence of chemical reaction of first order. References [8-10] discussed the effects of thermo diffusion (Soret effects) and diffusion-thermo (Dufour effects) on MHD mixed convection heat and mass transfer of an electrically conducting fluid. Mahantesh et al. [11] studied the boundary layer flow behavior and heat transfer characteristic in Walter’s liquid model-B fluid flow. Sharma et al. [12] discussed the unsteady MHD free convection heat and mass transfer of viscous fluid flowing through a Darcian porous regime adjacent to a moving vertical semi-infinite plate under Soret and Dufour effect.
Recently Kumar and Srivastava [13] examined the effects of chemical reaction on MHD flow of dusty viscoelastic (Walters’s liquid model-B) liquid with heat source/ sink. The interest of present investigation is to obtain analytical expressions for various profiles like velocity, skin friction for dusty fluid as well as dust particles and also temperature, concentration for dusty fluid. The effects of thermal diffusion parameter (Soret number), chemical reaction parameter etc. are discussed for different profiles.
2. Nomenclature
B0: Magnetic field
m: Magnetic field Parameter
 : Species concentration in the field
: Species concentration in the field
Pr : Prandtl Number
Cw: Concentration of the plate
Sc : Schmidt Number
C0 : Initial uniform concentration at 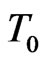
Tw : Plate temperature
Cp : Specific heat at constant pressure
 : Initial temperature
: Initial temperature
G : Acceleration due to gravity
t : Time
Gr : Thermal Grashof number
u,v: Velocities of dusty fluid and dust particle respectively
S : Source/sink parameter respectively in the x-direction
Gm: modified Grashof number
y : Co-ordinate axes as in normal to the plate
K : dimensionless chemical reaction parameter
A : Decay factor
K1 : Chemical reaction parameter
DT: Thermal diffusion coefficient
3. Mathematical Formulation
We consider the effects of thermal diffusion and chemical reaction on the unsteady dusty flow of an incompressible, slightly conducting, visco-elastic fluid between two heated porous infinite parallel plates (distance 2 h apart) under the influence of uniform magnetic field normal to the flow field in presence of heat source/sink. We assume x-axis along the flow in the mid-way of the plates and y-axis perpendicular to it. Let u, v be the velocities of dusty fluid and dust particles respectively in the direction of x-axis. The present analysis is based on the following assumptions:
1) The flow is in the direction of x-axis and is driven by a constant pressure  with negligible body forces.
with negligible body forces.
2) The dust particles are non-conducting, solid, spherical, and equal in size, uniformly and symmetrically distributed in the flow field and their number density 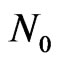 is constant throughout the motion.
is constant throughout the motion.
3) There is no externally applied electric field and the induced magnetic field is negligible.
4) Initially, when , the channel, walls as well as dusty fluid are assumed to be at the same temperature T0. The foreign mass is assumed to be present at low level and it is uniformly distributed such that it is everywhere C0.
, the channel, walls as well as dusty fluid are assumed to be at the same temperature T0. The foreign mass is assumed to be present at low level and it is uniformly distributed such that it is everywhere C0.
5) When t > 0, the temperature of the walls is instantaneously raised to TW and the species concentration is raised to CW.
6) There exists a chemical reaction in the mixture.
Under these assumptions and Boussinesq’s approximation with concentration, the equations governing the flow are:
 ….(1)
….(1)
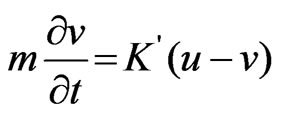 (2)
(2)
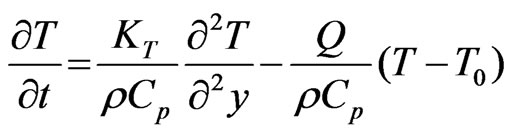 (3)
(3)
 (4)
(4)
(where the symbols have their usual meaning), at t = 0, the temperature and concentration level changes according to the following laws:
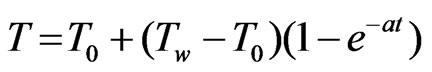

The initial and boundary conditions relevant to the problem are:
t = 0: u = 0 = v,T = T0 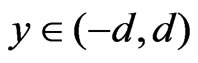
t > 0: u = 0 = v,  ,
,
 for y = –d u = 0 = v,
for y = –d u = 0 = v,  ,
,
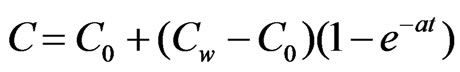 for y = d(5)
for y = d(5)
We introduce the following non-dimensional quantities,
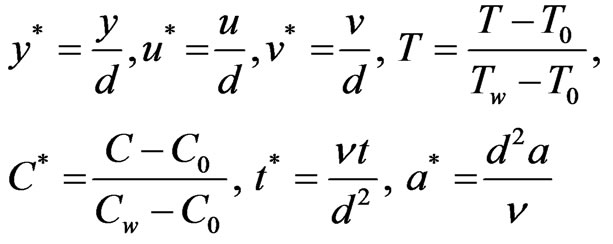
Introducing these non-dimensional quantities, Equations (1), (2), (3) & (4) reduce to
 (6)
(6)
 (7)
(7)
 (8)
(8)
 (9)
(9)
Now initial and boundary condition (5) according to new system becomeT = 0: u = 0 = v, T = 0 
t > 0: u = 0 = v, T = 1 – e-at, C = 1 – e-at, for y = –1 u = 0 = v, T = 1 – e-at, C = 1 – e-at, for y = 1 (10)
where,  (mass concentration of dust particle)
(mass concentration of dust particle)
M (Hartmann number) 
W (relaxation time parameter for particles) 
Gr (grashof number) 
Gm (Modified grashof number) 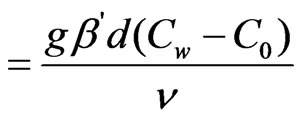
Sc (Schmidt number) 
S (heat source/sink parameter) 
K (Chemical reaction parameter) 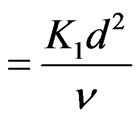
 (Visco-elastic parameter),
(Visco-elastic parameter), , Pr (Prandtl number)
, Pr (Prandtl number)
 (Thermal diffusion parameter)
(Thermal diffusion parameter)
4. Method of Solution
To solve the Equations (6) to (9) subject to the boundary conditions (10), according to I. Pop [14], we assume
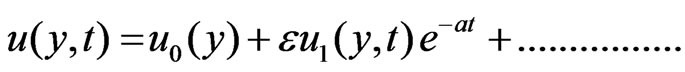

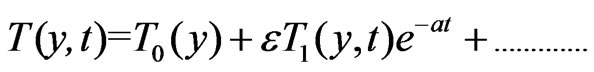
 (11)
(11)
Substituting the equations like (11) into the Equations (6) to (9) and equating harmonic and non-harmonic terms, we get the following set of equations.
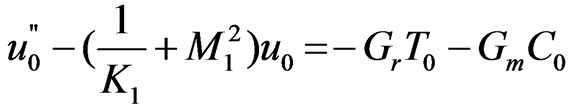 (12)
(12)
 (13)
(13)
u0 = v0 & u1 = v1 (1-aw)(14)
 (15)
(15)
 (16)
(16)
 (17)
(17)
 (18)
(18)
Where dashes represents differentiation w. r. to y.
Boundary conditions are reduced to:

 (19)
(19)
Solutions of the Equations (12) to (18) under the boundary conditions (19) after substituting in (11), we have:


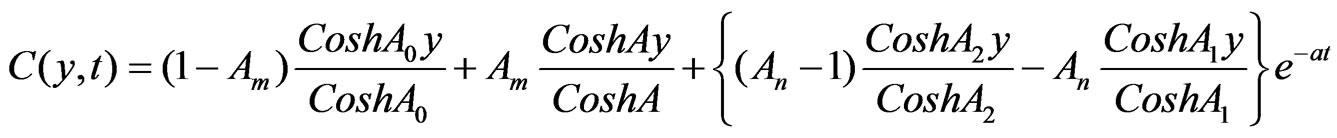

4.1. Skin Friction
Let  and
and  be the skin friction for dusty fluid and dust particles respectively then we have:
be the skin friction for dusty fluid and dust particles respectively then we have:


4.2. Appendix
 ,
, ,
, ,
, ,
,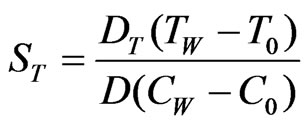 ,
, ,
,  ,
,
 ,
, ,
, ,
, ,
, ,
, 
5. Results & Discussion
Numerical solutions for velocity profile, skin friction for dusty fluid as well as dust particles and also temperature field, concentration profile for dusty fluid have been calculated. The values of different parameters and their effects on velocity, Temperature, concentration and skin friction have been displayed through graphs.
A temperature field has been represented in Figure 1, which indicates the effects of heat source/sink parameter and Prandtl number.
5.1. Temperature Field for Different Values of S and Pr (t = 1, a = 0.2)
It is observed that increasing values of heat source/sink parameter and Prandtl number decreases the temperature. Also we see that the temperature is minimum at the centre of the channel (y = 0) and increasing towards the plates.

Figure 1. Temperature filed for different values of S and Pr.
5.2. Concentration Profile for the Different Values of K and ST (a = 0.2, S = 0.2,t = 1, Pr = 0.71, Sc = 0.6, D = 1)
Observation of Figure 2 is increasing value of thermal diffusion parameter (Soret number) and chemical reaction parameter decreases the concentration. Concentration is minimum at the centre of the channel (y = 0) and increasing towards the plates.
5.3. Velocity Profile for the Different Values of K and ST (a = 0.2, S = 0.2, t = 1, Pr = 0.71, Sc = 2, D = 1, w = 0.5, E = 1, K1 = 10, Gm = 5, Gr = 10)
From Figures 3 and 4 we observe that increasing value of thermal diffusion parameter (Soret number) increases the velocity of dusty fluid and dust particles while chemical reaction parameter decreases the same. Also Figures 3 and 4 bears that the velocity is maximum at the centre of the channel and decreasing towards the plates.
5.4. Skin Friction Profile for Fluid and Dust Particles:(a = 0.2, S = 0.2, t = 1, Pr = 0.71, Sc = 2, D = 1,w = 0.5, E = 1, K1 = 10, Gm = 5, Gr = 10 )
Skin friction for different values of ST (M = 3, K = 0.4,
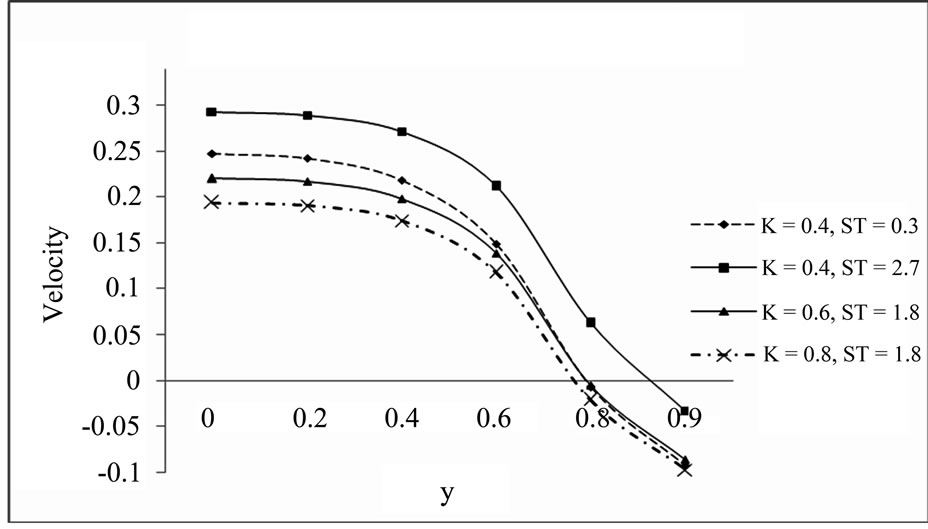
Figure 3. Velocity profile for dusty fluid.

Figure 4. Velocity profile for dust particle.
S = 0.3):
Skin friction for different values of S, (M = 3, K = 1, ST = 1.4):
Skin friction for different values of K (M = 3, ST = 2.7.4, S = 0.3): Skin friction for different values of M (ST = 1.4, K = 1, S = 0.4):
The results displayed in Figures 5.1-5.4 are as, the increasing value of thermal diffusion parameter and heat source/sink parameter decreases the skin friction of dusty fluid and dust particles. Increasing value of chemical re-
action parameter and magnetic field parameter increases the skin friction of dusty fluid and dust particles.
6. Conclusions
The theoretical and numerical solutions are obtained for different profiles. From graphical representations, we have the following observations:
1) Velocity and skin friction of the dust particles behaves same as dusty fluid.
2) Increasing value of y increases the temperature, concentration while decreases the velocity of dusty fluid and dust particles.
3) Velocity of dust particles is less than velocity of dusty fluid and skin friction of dust particles is greater than that of dusty fluid.
4) Increasing values of thermal diffusion parameter (Soret number) decreases the concentration, skin friction while increases the velocity of dust particles and dusty fluid.
5) Increasing values of magnetic field parameter increases the skin friction for both the dusty fluid and dust particles.
6) Increasing values of heat source/sink parameter decreases the skin friction for the dusty fluid as well as dust particles.
7. Acknowledgements
The author is sincerely thankful to the reviewers for the critical comments and suggestions to improve the quality of the manuscript.