A Novel Decoder Based on Parallel Genetic Algorithms for Linear Block Codes ()
1. Introduction
The error correcting codes began with the introduction of Hamming codes [1] in the same period that the remarkable work of Shannon [2]. They consist in correcting data corruption when saved in storage media (erasure CD/ DVD, etc.) or transmitted over noisy communication channel. Figure 1 shows the canonical system diagram of numerical communication.
The encoder takes the information symbols and adds to them redundancy symbols, carefully chosen such that a maximum of errors, which are infiltrated throughout the process of signal modulation, noisy transmission channel, and demodulation, can be corrected. The resulting binary code word is then transmitted over the noisy and memoryless channel under assumption that the sending messages are independent from the added noise. At the reception, the decoder attempts, given channel observations and using the redundancy symbols, to find the most probable message. The techniques used by the decoder are diverse. The most optimal criterion is Maximum Likelihood [3]. Given its high complexity (computation time, memory occupation), other suboptimal techniques with acceptable performance are used in practice like Turbo codes [4] and LDPC [5]. Several other decoders developed were inspired from the artificial intelligence field as Han decoding which using algorithm A* [6], Genetic Algorithms (GAs) [7] and Neural Networks
[8]. In 2007, it was shown that decoders based on GAs have good performance and time complexity lower than those of classical algebraic decoders [9]. In 2008, the performance of these decoders has been further improved by using iterative decoding for product block codes in two dimensions [10]. In 2012, we made an extension of concatenated codes by passing to three dimensions [11]. In this last work, we have proposed two iterative decoding algorithms based on GAs, which can be applied to any arbitrary 3D binary product block codes, without the need of a Hard-In Hard-Out decoder.
The first decoder outperforms the Chase-Pyndiah [12] one. The second algorithm, which uses the List-Based SISO Decoding Algorithm (LBDA) based on order-i reprocessing [13], is more efficient than the first one. We have also showed that the two proposed decoders are less complex than both Chase-Pyndiah algorithm for codes with large correction capacity, and LBDA for large i parameter.
All these proposed decoders have been designed to run on a single processor machines. Their instructions are executed sequentially and then so slowly. In addition, we do not take advantage of the parallel nature of GAs, which is a major advantage related to their exploration and convergence. So, the aim of this new work is to overcome these drawbacks by applying Parallel Genetic Algorithms (PGAs) to decoding linear block codes. Thus,

Figure 1. The canonical diagram of numerical communication.
we have developed a new decoder using parallel genetic algorithms, which runs on a parallel computer with multiple processors and a shared memory, or on a distributed system. So, it reduces the time complexity and increases little performance.
This paper is organized as follows. Section 2 presents some background on Linear Block Codes, Parallel System, and Genetic Algorithms. Section 3 describes the proposed Parallel Genetic Algorithms Decoder (PGAD), studies its time complexity and compares it with the one of SGAD. In Section 4 we discuss the simulation results obtained for PGAD. Finally, we give in Section 5 our conclusions and perspectives of this work.
2. Background
2.1. Linear Block Codes
Let  be the binary alphabet and
be the binary alphabet and 
The set of all words of length n i.e.:

A linear code C of length n on  is a subspace of the vector space
is a subspace of the vector space  [14]. i.e.:
[14]. i.e.:

Let  such that
such that 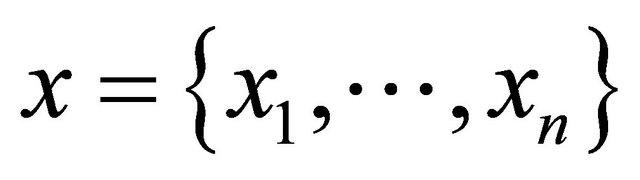 and
and
 . The Hamming distance between x and ynoted
. The Hamming distance between x and ynoted , is defined by:
, is defined by:

The minimum Hamming distance d of a code C is the Smallest non zero distance between all its vectors, taken two by two. i.e.:
 (1)
(1)
Let  be the dimension of code C. C is then said
be the dimension of code C. C is then said  -linear code. The code rate is the ratio
-linear code. The code rate is the ratio 
Let  be a basis of C. Since
be a basis of C. Since , Then length (bi) = n. The matrix G for which rows are the basis vectors is called generating matrix of the code C. It can be written as:
, Then length (bi) = n. The matrix G for which rows are the basis vectors is called generating matrix of the code C. It can be written as:

Thus, we have:
 i.e.
i.e. 
 such that
such that  i.e:
i.e:

2.2. Parallel Systems
The choice of parallel machines or distributed systems is more imposed for applications requiring a very high processing power and/or a big memory space. There are plenty of parallel systems which are classified as below [15].
2.2.1. Taxonomy of Parallel Systems
These systems have been classified by Flynn (1972) according to two independent concepts: the stream of instructions and the stream of data used by these instructions. There are four possible combinations:
• SISD (Single Instruction, Single Data): The machine executes one instruction on one data at each clock cycle. It is not really a parallel machine but a classical computer (Von Newman).
• SIMD (Single Instruction Multiple Data): A processor having a single Control Unit (CU) and multiple Arithmetical and Logical Units (ALUs) executes the same instruction on different data at each clock cycle.
• MISD (Multiple Instruction, Single Data): Systems running multiple instructions on the same data at each clock cycle.
• MIMD (Multiple Instruction Multiple Data): These systems are multiple independent processors i.e. each processor has its CU and its ALU. At the same clock cycle, each processor executes a different instruction on a different data. These instructions can be synchronous or asynchronous. The majority of parallel systems are MIMD. The MIMD system can be either a Multiprocessor or a Multi-computer or a hybrid of them. We explain in the next subsections the architecture of each one.
2.2.2. Multiprocessor
It is a MIMD parallel system with certain number of autonomous processors (CU+ALU) and a single shared memory. i.e. All processors use a common physical memory which composed of several memory blocks Figure 2. These blocks are interconnected with the processor and between them [15].
If two processors want to communicate, it suffices that the first one writes data (or message) in the memory and the other one recuperates it. So their programming is easy since the programmer does not have to focus on the explicit communication (message exchange) between the different processors. These allowed multiprocessors making a great success. However, it would be difficult to build a multiprocessor when the number of its communicating elements (processors and memory blocks) is very important. Indeed, the interconnection of all these elements is not always an easy task.
2.2.3. Multi-Computer
A multi-computer is also a MIMD system but relatively simple to build. It contains a number of computers (CU + ALU + private memory) linked together by an interconnection network. Each computer has its own memory Figure 3. This reduces significantly the number of elements to be interconnected. The communication between computers is achieved by exchanging messages as primitives Send/Receive, programmed and integrated by the programmer in its application [15]. This may complicate more his task. The following points must be taken into account for each parallel programming:
• For an efficient communication between different elements (processors and memory blocks) of a parallel or distributed system, the suitable choice of the topology, routing and switching mode of its interconnection network affects its performance remarkably.
• To benefit from the advantages of a multiprocessor and those of a multi-computer and minimize the disadvantages of each one of them, hybrid systems have been designed.
• To take advantage of parallel systems, we must execute on them parallel programs or containing a significant part of parallel instructions.
2.3. Genetic Algorithms
The Genetic Algorithm (GA), initiated in 1970 by Holland [16] is an Evolutionary Algorithm (EA) inspired from the natural biological evolution. It use search stochastic techniques to solve problems not having an analytical resolution or when the time to resolve them by classical algorithms is not reasonable [17]. Their applications cover, in addition to error correcting codes in telecommunication, several other fields as optimization, artificial intelligence, economic markets, etc. As shown in algorithm below [18], an EA especially a GA has an iterative character:

Figure 2. A multiprocessor with 16 processors sharing a commonmemory.

Figure 3. A multi-computer with 16 interconnected processors where each one has its own memory.
t=0;
initialize and evaluate [P(t)] ;
while not stop-condition do P’(t)=variation [P(t)] ;
Evaluate [P’(t)] ;
P(t+1) =select [P’(t), P(t)];
t=t+1;
end while.
It generates an intermediate population  by applying variation operators (often stochastic) on individuals (which may be here, information sequences or codewords) of the current population P(t). Then, it evaluates the quality (of being solution) of individuals from
by applying variation operators (often stochastic) on individuals (which may be here, information sequences or codewords) of the current population P(t). Then, it evaluates the quality (of being solution) of individuals from  using a criterion known as fitness. It finally creates the new population P(t+1) in which individuals are selected from those of
using a criterion known as fitness. It finally creates the new population P(t+1) in which individuals are selected from those of  and eventually from P(t). The process is repeated until the stopping condition is satisfied. In general, the process is stopped when the optimal solution is found or when the maximum number of iterations is reached.
and eventually from P(t). The process is repeated until the stopping condition is satisfied. In general, the process is stopped when the optimal solution is found or when the maximum number of iterations is reached.
The Genetic Algorithms can be singles (SGA) or Parallels (PGA).
2.3.1. Single Genetic Algorithms
The previous general algorithm can be adapted in SGA as follows:
Generate an initial population of n individuals randomly;
while not stop-condition do Calculate the fitness f (x) for any individual x;
while not Filled-New-Population do Select two parent individuals;
Cross them to have a new(s) individual(s);
The new individuals undergo eventual mutations;
Insert the new individual in the new population;
end while
Replace the old population by the new one;
end while.
The three classical operators inspired from natural evolution to generate a new population from the current one in both SGA and PGA are selection, crossover and mutation:
• The selection operator describes how to select the parents in the current population to cross them and generate new individuals (offspring) which will be inserted in the new population. The individuals are sorted in ascending order of their fitness to give more chances to the best ones (fittest) to be selected (assuming that better parents reproduce better children). However, there are cases where the crossing of bad parents can generate good offspring. The most popular selection methods are: Proportional, Linear Ranking, Whitley’s Linear Ranking and Uniform Ranking [19].
• The crossover operator generates new individuals inheriting from their parents. i.e. Their genes are a mixture of those of their parents. There are several crossing techniques that can be either generic (robust) i.e. applied in a wide variety of problems, or specific to particular problems, or hybrid techniques combining generic and specific ones.
• As in natural evolution, the genes of some individuals may undergo changes (mutations). This occurs in very rare cases. The mutation plays a very important role in the convergence of SGA and PGA algorithms. Indeed, it will prevent their premature convergence by guiding them to explore other more promising areas and avoid a local optimum.
2.3.2. Parallel Genetic Algorithms
The PGAs are GAs running on parallel systems discussed in the second subsection.Their purpose is not only accelerating the convergence and/or use a large memory space but also improve the performance. There are two models of PGAs: 1) Island model (or network model) which runs an independent GA with a sub-population on each processor, and the best individuals are communicated either to all other sub-populations or to neighboring population [20]; 2) Cellular model (or neighborhood model) which runs an individual on each processor, and cross with the best individual among its neighbors [21]. In fact, the second model is a particular case of the first one. Indeed, its population is reduced to a single individual on each processor.
The general algorithm of PGAs is given below:
Generate an initial population of n individuals randomly;
while not stop-condition do Calculate the fitness f (x) for any individual x;
if Interval-Exchange then Exchange of individuals;
end if
while not Filled-New-Population do Select individual parents;
Cross them to make new people;
New individuals undergo eventual mutations;
Insert new individuals in the new population;
end while.
Replace the old population by the new one;
end while.
3. The Proposed Parallel Decoder Based on Genetic Algorithms
This work is a parallelization of the decoder that we have already used in [9,10], and [11] by exploiting some techniques of parallel genetic algorithms used in other domains like Optimization and Artificial Intelligence. It can be run on a multiprocessor where the data exchanged are saved in global or shared variables, or on a multi-computer which exchange data between its processors via a network.
Let 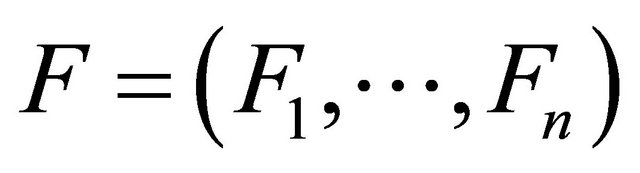 and
and  be respectively the fading vector and the received sequence (associated to the transmitted sequence) at the decoder input of a binary linear block code C(n,k,d) with a generator matrix G. The parameters Np, Ne, Nc, Nm, Ns, Ng are respectively the population size, elite number, offspring number, migrant number, processor number and maximum number of generations such that
be respectively the fading vector and the received sequence (associated to the transmitted sequence) at the decoder input of a binary linear block code C(n,k,d) with a generator matrix G. The parameters Np, Ne, Nc, Nm, Ns, Ng are respectively the population size, elite number, offspring number, migrant number, processor number and maximum number of generations such that  is a positive integer.
is a positive integer.
3.1. The PGAD Algorithm
The sub-algorithm which will run in parallel on each processor is given below:
• Step 0: Initialization
• Sort the elements of the received vector R in descending order of their magnitude to produce another vector R(1) i.e. find a permutation π1 such that
 and
and . This will put reliable elements in the first ranks.
. This will put reliable elements in the first ranks.  is the permutation of F by
is the permutation of F by  i.e.
i.e. . Then, permute G by
. Then, permute G by  to produce G′ such that the first k columns of G′ are linearly independent i.e.
to produce G′ such that the first k columns of G′ are linearly independent i.e.
 . The two vectors
. The two vectors  and
and  are permuted by
are permuted by  to
to  and
and 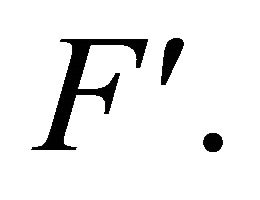 So,
So,
 and
and
 , with
, with
 .
.
• Quantize the first k bits of  to obtain binary vector r and randomly generate Np − 1 information vectors of k bits each one. These vectors form with vector r the initial population of Np individuals
to obtain binary vector r and randomly generate Np − 1 information vectors of k bits each one. These vectors form with vector r the initial population of Np individuals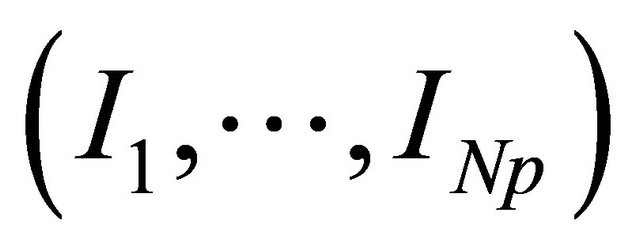 ;
;
Step 1: Reproduction
gen←0 (gen is the current generation number).
While (gen < Ng) do
• Encode individuals of the current population, using G′ to obtain code words: Ci = IiG′ (1 ≤ i ≤ Np);
• Compute individual fitness, defined as Euclidian distance between Ci and :
:
• 
• Sort the current population individuals in descending order of their fitness;
• Copy the Ne best individuals (elites) from the current population to the new one;
• Select parents from the Np − Ne individuals of the current population;
• Cross with probability pc the selected parents to generate Nc new individuals;
• Mutate the new individuals with a probability pm if their parents are crossed;
• Insert these Nc new individuals with their fitness in the new population Figure 4;
• Send the best  individuals (with their fitness) to the new populations of Ns − 1 other processors as shown in Figure 5;
individuals (with their fitness) to the new populations of Ns − 1 other processors as shown in Figure 5;
• Receive Nm migrant elites (with their fitness) from the previous population of each Ns − 1 other processors, to complete the new population as shown in Figure 6;
• Replace the current population with the new one;
• gen←gen+1;
end while
Step 2: Decision
Get the best individuals  of last populations of all processors. The best one D′ of them is the closest to R′. i.e.
of last populations of all processors. The best one D′ of them is the closest to R′. i.e. .
.
So, the decided codeword is .
.

Figure 4. The ith processor which works on the current population to give the next one.

Figure 5. In a given generation, the ith processor sends its best Nm individuals to other processors.

Figure 6. In a given generation, the ith processor receives the best Nm individuals from each other processor.
The flowchart of the previous algorithm is illustrated in Figures 7 and 8.
3.2. The PGAD Characteristics
The main elements characterizing a basic PGA are [19]: evolution mode, reproduction operators (crossover and mutation), selection and replacement policy of individuals (local and foreign) and migration.
3.2.1. Evolution Mode
It defines the granularity of the evolution step in a sub-algorithm of the PGA. i.e. how the new population is created from the current one. There are two techniques that are often used. The first one is the generational GA (GGA) where the new population replaces all the old ones. The second technique inserts only a few new (generated) individuals in the current population. In our implementation, we have used the GGA evolution mode with elitism.
3.2.2. Reproducing Operators
To generate Nc individuals 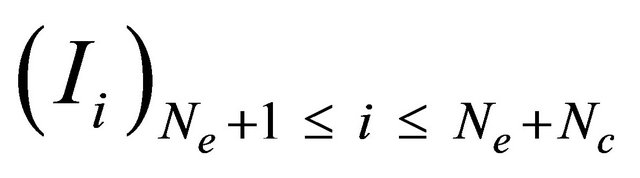 in the new population, we have used, like in our works [10], and [11], these operators:
in the new population, we have used, like in our works [10], and [11], these operators:

Figure 7. The flowchart of the proposed PGAD sub-algorithm running on the ith processor.

Figure 8. The codeword decision flowchart of the proposed PGAD algorithm.
• Selection of two individuals as parents (P,Q) using the following linear ranking:
 (2)
(2)
where weighti is the ith individual weight and weightmax is the weight assigned to the fittest (closest) individual.
• Let pc, pm be respectively, the probabilities of crossover and mutation, and let Rand be a uniformly random value between 0 and 1, generated at each time.
if Rand < pc then

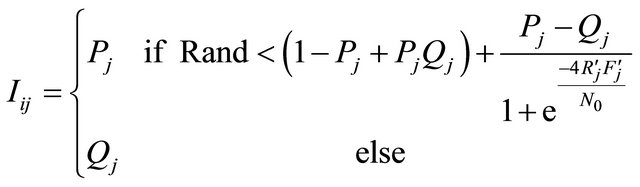 (3)
(3)
and then

else

end if.
We note that on an AWGN (Additive White Gaussian Noise Channel) channel, we have
 .
.
3.2.3. Selection and Replacement Strategies
They define the selection of individuals to replace in the current population of a sub-algorithm PGA and those to migrate from other processors. The individuals can be replaced by new local ones or by the migrant ones:
• The main replacement policies are [19]: 1) Inverse Proportional; where the worst individual is more likely to be replaced; 2) Uniform Random; where all individuals have the same chance of being replaced; 3) Worst; where the worst individual is always replaced. In some problems, it is replaced only if it is worse than the new one; 4) Generational; where the entire current population is replaced by a new one. In our work, we keep the best local individuals (elitism) and the bad ones are replaced by new local offspring and by the migrants from other processors.
• There are two cases to choose migrant individuals: choose the best ones, or choose them randomly. In our algorithm, we chose the best migrants.
3.2.4. Migration
This is an operation that helps to diversify and enrich the new population of a sub-algorithm which runs in a processor by migrant individuals from other cooperator processors of the PGA. There are two parameters characterizing the migration operation: Migration Gap and Migration Rate. The first one specifies the frequency of exchange of individuals. i.e. The number of steps that a sub-algorithm must run before sending or receiving migrant individuals. It can also specify the probability of migration at each stage. The second migration parameter defines the number of exchanged individuals (migrants). The exchange (send/receive) of individuals is done in two modes: synchronous or asynchronous.
The synchronous mode suspends, periodically, the execution of a sub-algorithm of the PGA and waits for the receiving migrant individuals from other nodes before continuing its execution. In asynchronous mode, the sub-algorithm does not wait. Once the migrant individuals arrive, it deals with them.
In our algorithm, we send/receive at each new population the  first best individualsto/from every other processor according to the asynchronous mode. To reduce the number of messages that flow through the network connecting processors, the number of migrant individuals should be less than the number of individuals locally generated for each new population. i.e.
first best individualsto/from every other processor according to the asynchronous mode. To reduce the number of messages that flow through the network connecting processors, the number of migrant individuals should be less than the number of individuals locally generated for each new population. i.e.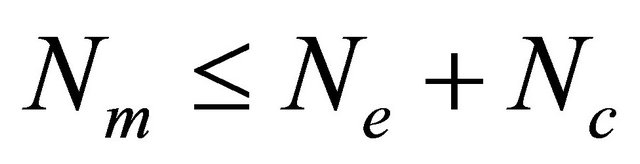 .
.
3.2.5. Heterogeneity
A PGA is called homogeneous if its nodes run the same type of algorithm. Otherwise, it is called heterogeneous. Our PGAD is homogeneous. Indeed, all nodes are symmetric and perform the same genetic algorithm having same parameters and operators.
3.3. PGAD Time Complexity
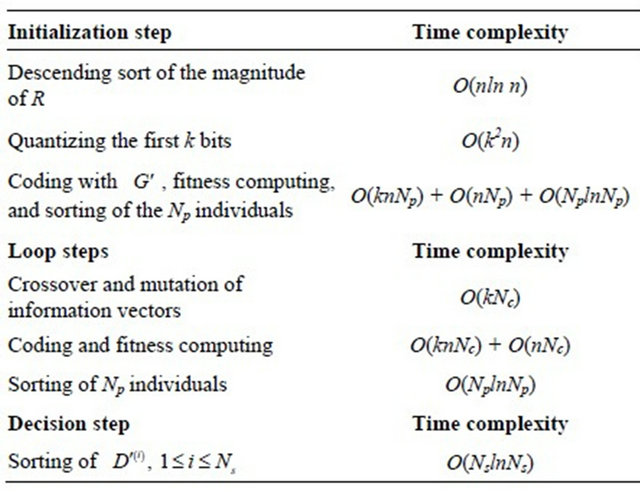
We give in Table 1 the complexity of the different stages of the proposed decoding algorithm PGAD in the order oftheir appearance in the flowcharts of Figures 7 and 8 before deducting its global complexity.
We note that:
• The crossover operation will be made almost always, since its probability is close to 1. So its time complexity is O(kNc).
• The complexity of mutation operation is neglected. Indeed, this operation will occur rarely since its probability is close to 0.
The total time complexity of PGAD is then:
Table 1. Time complexities of different steps of the PGAD.
 (4)
(4)
From the formula (4), it is clear that the complexity of PGAD is lower than that of SGAD. Indeed, there are terms that are common to both decoders (initialization and sorting at the end of the loop). The term NslnNs can be neglected when the processor number is small. The difference between SGAD and PGAD consists in the crossing, coding, and fitness computing in the loop. For each generation, we must cross parents to have Np ‒ Ne new individuals in the case of SGAD against only Nc in PGAD (Nc < Np ‒ Ne). Likewise we encode in the loop only Nc individuals in our decoder against Np ‒ Ne in SGAD. For the fitness in the loop, it is also computed for Nc individuals instead of Np ‒ Ne.
From the foregoing, we can summarize the advantages of our decoder as follows:
• Improvement of performance. Indeed, It corrects errors better than simple algorithms studied in [9,10] as shown in simulation section.
• Reducing the time complexity of the decoding process: 1) It is run in parallel on multiple processors for almost the same number or lower of total individuals (NgNp) used in a single decoder; 2) It reduces the time of encoding and fitness computing, since the algorithm receives (Np − Ne − Nc) migrant individuals (encoded) with their fitness already computed; 3) It reduces the reproduction time since the number of parents to cross is reduced to Nc(Nc < Np − Ne).
4. Simulation Results
Our PGAD is run on 4 processors (Ns = 4). To study the performance of the presented PGAD decoder, we have simulated a binary communication system with BPSK modulation and both AWGN and Rayleigh fading channels. We give in this section, the impact of each parameter Ng, Np, pc, pm, Ne, Nc and code rate on the performance of our decoder and we finish with a comparison with the SGAD decoder. The chosen code is the linear block BCH(63,30,14) code. The minimum number of sent erroneous frames is 30. The performance will be given as figures showing the Bit Error Rate (BER) versus the energy per bit to noise power spectral density ratio Eb/N0.
The figures corresponding to each channel are given in Table 2.
4.1. Effect of Generation Number and Population Size
Generally, increasing the number of evaluated code
Table 2. Simulation figures corresponding to each channel.

words NpNg, the probability to find the codeword closest to the input sequence becomes high. This makes it possible to improve the BER performances. The effect of increasing the number of evaluated code words on the BER improvement for code BCH(63,30,14) at the 12th iteration is presented in Figures 9 and 10. The values Ng = 100 and Np = 100 can be the optimal values in a large range Eb/N0. The other genetic parameters for the first optimization are: Np = 100, Nc = 80, Ne = 5, pc = 0.99, pm = 0.03 and Ng = 100, Nc = 80, pc = 0.99, pm = 0.03 for the second one.
4.2. Crossover Rate Effect
The crossover is a very important operation insofar as it allows a large exploration, and an effective exploitation. In Indeed, it creates new individuals may be good solutions to the problem. For most problems, the probability of crossover is high. This is the case also for the error correcting. The Figure 11 shows that among the studied probabilities pc= 0.99 offers the best performance. For this simulation, we have fixed the other parameters as follows: Ng = 10, Np = 100, Nc = 80, Ne = 5, and pm = 0.03.
4.3. Mutation Rate Effect
The effect of mutation rate for BCH(63,30,14) is depicted in Figure 12. It is shown that pm = 0.03 is the optimal BER value for all SNRs. One reason of this value close to 0 may be the stability of members in vicinity of optima for low mutation rates. The fixed values are: Ng = 100, Np = 100, Nc = 80, Ne = 5, and pc = 0.99.
4.4. Elite Number Effect
Among the best individuals of the current population, some may survive and move to the new population. This can be justified by the fact that their elitism may give birth to other best descendants. As shown in the Figure 13, the greater the number of elites survived, more performances improve. However, when we exceed five elites the performances begin to decline. We deduce that worse individuals can also create, by crossover and mutation, better individuals. So we choose Ne = 5. The fixed values for this simulation are: Ng = 100, Np = 100, Nc = 80, pc = 0.99 and pm = 0.03.
4.5. Offspring Number and Migration Rate Effects
The number of individuals migrating from each nodeis

Figure 9. Effect of the generation number for BCH(63,30,14).

Figure 10. Effect of the population size for BCH(63,30,14).

Figure 11. Effect of the crossover probability for BCH(63,30,14).
 So when this number decreases, the number of individuals created locally Nc increases. From the curves plotted in Figure 14, performances increase when Nc increases up to a threshold
So when this number decreases, the number of individuals created locally Nc increases. From the curves plotted in Figure 14, performances increase when Nc increases up to a threshold

Figure 12. Effect of the mutation rate for BCH(63,30,14).

Figure 13. Effect of the elite number for BCH(63,30,14).

Figure 14. Effect of the offspring number for BCH(63,30,14).
Nc = 80. We also note that when there is no exchange of individuals (Nc = 95 i.e. the number of migrant individuals is equal to 0) the performance is worse than with the exchange. The fixed values of parameters are: Ng = 100, Np = 100, Ne = 5, pc = 0.99 and pm = 0.03.
4.6. Code Rate Effect
We have studied the performance of the following BCH codes: (63,30), (63,39), (63,45), and (63,51). From the Figure 15, we note that when the rate decreases, performance increases. This is explained by the fact that when the code length n increases for the same dimension k; the number of redundancy bits (check) increases. i.e. it corrects better with more redundancy; which makes sense. In this simulation, we adopted the optimal values in Table 3 previously found.
4.7. Performance Comparison between PGAD and SGAD
We have studied the performance of our PGAD on a Gaussian channel AWGN and flat Rayleigh fading channel with flat fading using the same parameters in Table 3. We remark from Figures 16 and 17 that the parallel decoder not only reduces the time complexity, but also has good performance compared to simple decoder studied in [9] and just for 4 processors.
5. Conclusion
We have presented a new decoder based on parallel genetic algorithms which can be applied to any linear block code. The simulations show that it provides better performance than a decoder based on SGA and the gain is
Table 3. Time complexities of different steps of the PGAD.


Figure 16. Performance comparison between SGAD and PGAD on AWGN channel for BCH(63,30,14).

Figure 17. Performance comparison between SGAD and PGAD on Rayleigh channel for BCH(63,30,14).
about 0.7 dB with 4 processors only. This is due to its parallel architecture which can exploit and explore more individuals and avoid the premature convergence to local optimum. In addition, this decoder has a lower complexity because it runs on multiple processors simultaneously, and because it reduces the time of encoding and fitness computing, and the time of generation of new individuals. Its performance can be further improved by adjusting algorithm parameters and characteristics (processor number, topology, migration, selection and replacement, ...) and by parallelizing tasks running on the same processor, or by putting it in hybrid with other decoders. We could also envisage an iterative decoding based on PGAs.