Some Approximation in Cone Metric Space and Variational Iterative Method ()
1. Introduction
Fixed point theory has fascinated many researchers since 1922 with the celebrated Banach’s fixed point theorem. There exist a fast literature on the topic and this is a very active field of research at present (See [1-7]).
By using same definition and meaning in stating is also looking in [2] and [3] etc. we introducing the following results for needing. For convenience, the authors give the following definition and lemma (see the proof of theorem 3 [2])
Let 
always be a real Banach space, and 
be the subset of 
is called a cone, if and only if:
(i) 
is closed, nonempty, and 
(ii) 
(iii) 
Given a cone
we define a partial ordering 
with respect to 
by 
if and only if 
We shall write 
to indicate 
but 
while 
implies 
int
denotes the interior of
.
Definition 1.1 Let 
be a non-empty set in
, and suppose the mapping 
satisfies:
(i) 
for any 
and 
(ii) 
for all 
(iii) 
for all 
Then 
is cone distance on 
is called a cone metric space.
It is obvious that cone metric space generalize the metric spaces.
Definition 1.2 Let 
is said to be a complete cone metric space, if every Cauchy sequence is convergent in 
Let 
be a metric space. We denote by 
the family of non-empty closed bounded subset of 
Let 
be the Hausdorff metric on
. That is for
where 
is the distance from point 
to the sub-set 
An element 
is said to be a fixed point of a multi-valued mapping 
Lemma 1.3 Suppose that 
be a cone metric space and the mapping 
hold the sequence 
in 
satisfying the following conditions:
and that is
Then the sequence 
is a Cauchy sequence in
.
2. Several Common Fixed Point Theorems
In recent years, the fixed point theory and application has rapidly development. Huang and Zhang [2] introduced the concept of a cone metric space that a element in Banach space equipped with a cone which induces a nature order partial order. In the same work, they investigated the convergence and that inequality and they extend the contractive principle to in partial order set s with some applications to matrix equations and common solution of integral equations.
Such theorems are very important tools for proving the existence and eventually the uniqueness of the solutions to various mathematical models (integral and partial differential equations, variations inequalities etc.).
First, we state following some extend conclusion ([3, 4]). Next, authors consider the variation iterative method to some integral and differential equations, and effective method ([5-8]) for examples and numerical test as some Fig case.
Now we first give common fixed point Theorem in similar method for two operators to extend Theorem 2.1 [2] with one operator case. Assume that 
be a complete cone metric space.
Theorem 2.1 Let 
be a complete cone metric space, 
a normal cone with normal constant 
Suppose that mappings 
satisfies the Contractive condition
(2.1)
for each 
where 
is a constant 
Then 
has a unique common fixed point in 
And so for any 
the iterative sequence 
converges to the fixed point.
Corollary 2.2 Let 
and 
then we obtain that theorem 2.1 in [2].
In the same way, authors can extend theorem 4 [2], and omit again these stating.
3. Some Notes of Common Fixed Point
Theorem A (See Theorem 1 [3]) Assume that 
be a complete cone metric space. Let mappings 
satisfying following Lipchitz conditions for any 
(3.0)
where 
are nonnegative real value functions on 
such that
and that
Then there is a unique common fixed point in 
for 
and 
and for any 
the iterative sequence 
convergent to the common fixed point of 
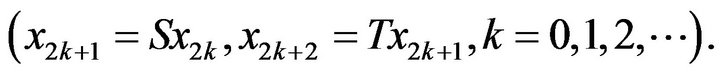
Remark in [3], the example 2 illustrate this effect of meanings with this Theorem (non-expansion mapping, not contractive case that have uniqueness common fixed point). Look for multiple-value mappings in some case [5].
We can easy note Theorem A. Now we give complete this fixed point problem below.
Theorem 3.1 Same as the assume of theorem 1 [3]. Let 
be a complete cone metric space, and there exists positive integer 
and mappings 
satisfying following Lipchitz conditions for any 
that is satisfy following inequality such that
(3.1)
where 
are non-negative real functions on 
If it holds, 
Then there is a unique common fixed point in 
for
.
Proof By the proof of theorem 1 [3] that we known that 
and 
has a unique common fixed point 
and 
from
then 
is also common fixed point of 
and 
Hence, we have 
by the uniqueness of them. In the same way, we know that 
that is, 
This 
is a common fixed point of
, and
We have 
On the other hand, if 
then clearly, 
in the same way, we know 
which a contradiction. So, we complete the proof of this theorem.
Theorem 3.2 Let 
be a complete cone metric space, and mappings 
satisfying following Lipchitz conditions for any 
that is satisfy following inequality (
nonnegative real constant)
(3.2)
and
If 
have not common fixed point each other, then the 
exist at least 
number fixed points in 
Proof By the theorem 1 [3], we known that 
and 
has a unique common fixed point 
that is 
and that in the same way,
Then S have at least 
number fixed points.
Corollary 3.3 Let 
more positive integer cases in theorem 3.1.
Remark 3.4 (see corollary 5 [3]) Assume that 
be complete cone metric space, and mappings 
satisfy following condition (
non-negative real constant):
(3.3)
And
then 
must have uniqueness common fixed point, and for any 
iterative sequence 
convergent to the common fixed point
Here example 2 in [5] for non-expansion mappings, also have common fixed point case with important meanings.
4. Common Fixed Point of Four Mappings
Many authors have extended the contraction mapping principle in difference direction. Some extension of Banach’s fixed point theorem through the rational expression form with it’s inequality. The purpose of this section, is to establish some common fixed point theorem for four mappings in this space.
Theorem 4.1 Assume that 
be a complete cone metric space, and mappings 
continuous and satisfying following conditions for any
and that inequality
(4.1)
Then 
have a unique common fixed point.
Proof Let 
be an arbitrary point of 
and from 
we can choose a point
such that 
Also 
we can choose a point 
such that 
In general, we can Choose 
and 
define a sequence 
in 
as follows,
Now, by (4.1) we have that
Similarly, we have
which implies that
Hence, it is well know that 
is Cauchy sequence. From the 
is complete, then there exists 
such that the 
convergences to 
in 
Since 
and 
are subsequences of 
then it will convergence to same point u.
Next, from these 
are continuous maps, we can obtain following results
It follows from 
then we have
and we get 
In the same reason,
we again obtain 
By (4.1), if 
then
this is a contradiction. Hence, we have that
Let 
then we obtain that
and
By (4.1), if 
then
we get 
It is a contradiction. Thus, 
Similarly,
we get 
It is also a contradiction. Therefore, 
By (4.1), if 
then
also a contradiction. Thus, we have
then this implies 
for common fixed point of
.
(Uniqueness) Let two points 
be the difference common fixed point of
.
By (4.1), we have
A contradiction in the above same reason, then this implies the uniqueness of common fixed point of
.
Remarks
(i) As 
we obtain special case.
(ii) 
(Identity map), 
we get some special case.
Theorem 4.2 Assume that 
be a complete cone metric space. Same as theorem 4.1, and satisfies these conditions below
for any
(4.2)
Then 
have a unique common fixed point.
Proof By theorem 4.1, we known that there is a unique fixed point 
in 
and 
Obviously, 
This completes the proof of theorem 4.2.
5. Some Notes for Multi-Valued Mappings
According the direction of [5], we give out some coincidence point theorem of maps to extend theorem 2.1 and theorem 2.3 [5].
Let 
be a strictly increasing function such that
(i) 
(ii) 
for each 
(iii) 
for each 
Now, we can easy obtain following theorems.
Theorem 5.1 Let 
be a complete metric space and 
be multi-valued maps
satisfying for each 
where
(5.1)
If 
have not common fixed point each other, then there exist at least 
number fixed points in 
Proof From theorem 2.1 [5], we known there exist 
in 
such that 
again for 
in 
The same way,
Since 
not equality each other, then S have at least 
number fixed point. This completes the proof.
Theorem 5.2 Let 
be a complete metric space and 
be multi-valued maps
and 
be a map satisfying
(i) 
(ii) 
is complete(iii) there exists a function 
such that
for every 
(5.2)
And for each 
(5.3)
If 
and 
have not coincidence point each other, then the 
and 
at least exist 
number coincidence points in 
Proof From theorem 2.3 [5], we known there exist coincidence point 
in 
such that 
in the same way, the coincidence point 
in 
with
Since
not equality each other, therefore 
and 
have at least 
number coincidence point. That is,
Then this completes the proof.
Corollary 5.3 Let 
be a complete metric space and 
be multi-valued maps
and 
be a map satisfying
(i) 
(ii) 
is complete(iii) 
for each 
where 
such that 
for every 
If 
have not coincidence point each other, then 
If we take 
we easy get these conclusion below, where 
is the identity map on 
Corollary 5.4 Let 
be a complete metric space and 
be multi-valued maps 
and satisfying for each
where 
such that 
for every 
If 
have not common fixed point each other, then the 
and 
exist at least
number points in 
That is case
Corollary 5.5 When
, for each 
Then we get also similar conclusion case: 
6. Solution of Integral Equation by VIM
Recently, the variation iteration method (VIM) has been favorably applied to some various kinds of nonlinear problems, for example, fractional differential equations, nonlinear differential equations, nonlinear thermo elasticity elasticity, nonlinear wave equations.
In this section, we apply the variation iteration method (simple writing VIM) to Integral-differential equations below (see [6,7]). To illustrate the basic idea of the method, we consider:
The basic character of the method is to construct functional for the system, which reads:
which can be identified optimally via variation theory, 
is the nth approximate solution, and 
denotes a restricted variation, i.e. 
There is a iterative formula:
of this equation
(*)
Theorem 6.1 (see theorem 3.1 [6]) Consider the iteration scheme 
and
. (6.1)
Now, for 
to construct a sequence of Successive iterations that for the 
for solution of integral Equation
.
In addition, we assume that
and 
then if 
the above iteration converges in the norm of 
to the solution of integral equation
.
Corollary 6.2 If 
and
then assume 
if 
the above iteration converges in the norm of 
to the solution of integral equation
.
Corollary 6.3 If 
and
then assume 
if 
the above iteration converges in the norm of 
to the solution of integral Equation
.
Example 6.4 Consider that integral equation
(6.2)
where
then if 
(See Figure 1(a)) then the iterative 
that convergent the solution of Equation (6.2) by corollary 6.2 of theorem 6.1. Therefore, we check that
From (6.1), we have that
Let
and
(See Figure 1(b), when n = 4).
The exact solution 
Then we obtain exact solution below
Remark The exact solution 
and approximate solution 
of Example 6.4 (See Figure 1(c)).
Example 6.5 We consider that integral equation
(6.3)
From (6.1), we have that
We take
The exact solution 
then we obtain exact solution below
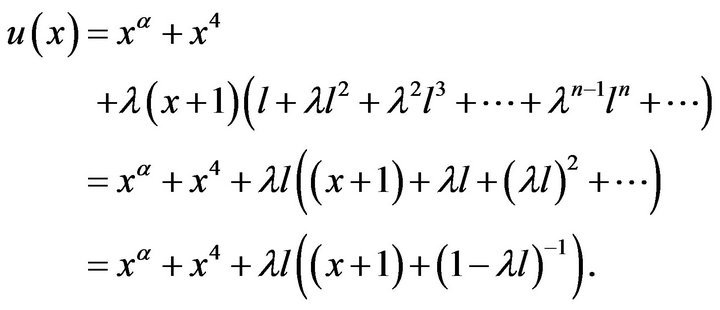
By corollary 6.2 of Theorem 6.1, where that
Then the iterative sequence is convergent to the exact solution of the Equation (6.3).
In fact,
then if 
the iterative sequence is convergent the solution of Equation (6.3).
Example 6.6 Consider that integral equation (
positive integer),
(6.4)
where 
and we have that
We can take that
(k-positive integer), and
Inductively, we have
Then by Theorem 6.1 and simple computation, we obtain that
then if 
the iterative is convergent the solution of integral equation (6.4) (Similar as examples case in [6, 7]).
7. Some Effective Modification and Numerical Test for [8]
In this section, we apply the effective modification method of He’s VIM to solve some integral-differential equations. In [6-8] by the variation iteration method (VIM ) simulate the system of this form
To illustrate its basic idea of the method, we consider the following general nonlinear system
the highest derivative and is assumed easily invertible, 
is a linear differential operator of order less than, 
represents the nonlinear terms, and 
is the source term. Applying the inverse operator 
to both sides of above equation, we obtain
The variational iteration method (VIM) proposed by Ji-Huan He (see [6-8] recently has been intensively studied by scientists and engineers. the references cited therein) is one of the methods which have received much concern. It is based on the Lagrange multiplier and it merits of simplicity and easy execution. Unlike the traditional numerical methods. Along the direction and technique in [4,8] we may get more examples below.
Example 7.1 (similar as example in [8]) Consider the following nonlinear Fredholm integral equation
(7.1)
Applying the inverse operator 
to both side of Equation (7.1), yields:
from 
So,
Inductively,
Then 
is exact solution of (7.1). The numerical results are shown in Figure 2.
Example 7.2 Consider the following Volterra-Fredholm integral-differential equation
(7.2)
Similar as example1 in this way, we easy get this solution.
According to the method, we divide
into two parts defined
and
By calculating this
So, we have
In fact, in this way
and
Writing
therefore, we have
Inductively,
And 
Hence the 
is the exact solution of (7.2).
Example 7.3 Consider the following integral-differential equation
(7.3)
where 
In similar example1, we easy have it .
According to the method, we divide
into two parts defined by
Figure 2. Figures of exact solution u(x) for Example 7.1.
Taking 
then we have
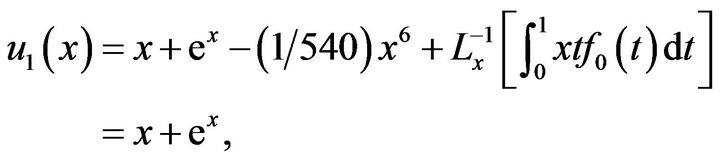
where 
And the processes,
Thus, 
then 
is the exact solution of (7.3) by only one iteration leads to a solution. The numerical results are shown in Figure 3.
Example 7.4 (See example 2 in [8]) Consider the following partial differential equation
(7.4)
Let that integer
The modified methods:
Applying the inverse operator to both sides of (7.4) yields
where 
Here, we divide 
into two parts defined by
Using the relation 
we obtain
and so on
Hence, 
is the exact solution of (7.4) and by only one iteration leads to that exact solution. Taking 
that is example 2 in [8].
The numerical results are shown in Figure 4.
Remark 7.5 Some solving integral-differential equations by VIM may see [9], and that some random Altman type inequality for fixed point results see [10].
The fixed point results of Multi-value mapping are also discussed in [11].
Remark 7.6 By [12], the authors consider the mixed problem for non-linear Burgers equation:
(7.5)
The authors point out the problem describes physic phenomenon of motive quality and conservation of law in dynamic problem, it is important model in flow mechanics. Where 
express the velocity of flow body,
Figure 3. Figures of exact solution u(x) for Example 7.3.
and 
express the constant of motive flow body,
-initial function.
Burger’s equation has attracted much attention. The approximation solution for this Burger’s equation is also interesting tasks.
8. Concluding Remarks
In this Letter, we give out new fixed point theorems in cone metric space and apply the variation iteration method to integral-differential equation, and extend some results in [3,6-8]. The obtained solution shows the method is also a very convenient and effective for some various non-linear integral and differential equations, only one iteration leads to exact solutions.
Recently, the impulsive differential delay equation and stochastic schrodinger equation is also a very interesting topic, and may look [11] etc.
9. Acknowledgements
This work is supported by the Natural Science Foundation (No.07ZC053) of Sichuan Education Bureau and the key program of Science and Technology Foundation (No.07zx2110) of Southwest University of Science and Technology.
The authors would like to thank the reviewers for the useful comments and some more better results.