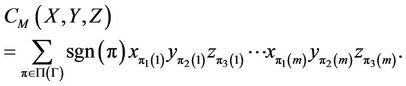Let  be a finite directed graph with multiple edges allowed, and let
be a finite directed graph with multiple edges allowed, and let  denote the vertex set of
denote the vertex set of  and
and  the edges set of
the edges set of . Let
. Let  and
and  be the functions from
be the functions from  to
to  defined by
defined by 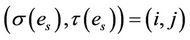 where es is an edge from vertex i to vertex j. For a vertex
where es is an edge from vertex i to vertex j. For a vertex  we put
we put
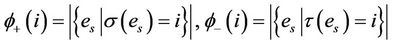
and

We say that  is an Eulerian path of
is an Eulerian path of 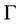 if
if  is an element of Sym(d) (the symmetric group acting on the set
is an element of Sym(d) (the symmetric group acting on the set  and
and 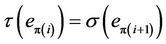 for
for .
.
It is well known that a connected graph  has an Eulerin path starting at vertex p and ending at vertex q if and only if one of the following two conditions applies:
has an Eulerin path starting at vertex p and ending at vertex q if and only if one of the following two conditions applies:
1) 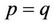 and
and  for each
for each ;
;
2)  and
and ,
,  and
and  for each
for each .
.
A directed connected graph  with fixed vertices p and q is called Eulerian if either condition 1) or 2) is satisfied. We note that if
with fixed vertices p and q is called Eulerian if either condition 1) or 2) is satisfied. We note that if  is an Eulerian graph of type (b), then the vertices p, q are uniquely determined, but in the other case we may choose any vertex
is an Eulerian graph of type (b), then the vertices p, q are uniquely determined, but in the other case we may choose any vertex . For an Eulerian graph
. For an Eulerian graph  denote by
denote by

2. Main Results
Let  be an Eulerian graph with d edges
be an Eulerian graph with d edges 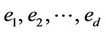 and distinguished points p and q. the polynomial
and distinguished points p and q. the polynomial  associated with
associated with  is defined as follows:
is defined as follows:

Thus  is a multilinear polynomial in the set
is a multilinear polynomial in the set 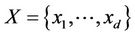 of non-commuting indeterminates.
of non-commuting indeterminates.
Let 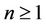 be an integer, C a commutative ring with 1 and
be an integer, C a commutative ring with 1 and  a set map where the
a set map where the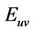 ’s are the standard matrix units over C. It is clear that T can be viewed as a substitution. we shall define a directed graph
’s are the standard matrix units over C. It is clear that T can be viewed as a substitution. we shall define a directed graph  induced from
induced from  by T. First consider the directed graph on the vertex set
by T. First consider the directed graph on the vertex set  with edge set
with edge set 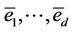 where
where ,
,  and
and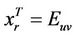 . Now we define
. Now we define  by restricting the vertex set to
by restricting the vertex set to . We note that the graph so obtained need by no means be connected let alone Eulerian. If it is Eulerian however, by construction
. We note that the graph so obtained need by no means be connected let alone Eulerian. If it is Eulerian however, by construction  has at most
has at most  min
min  vertices, where
vertices, where , i.e.,
, i.e.,  for all
for all 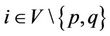 and
and  ,
, . Those elements of
. Those elements of  which do lift to an Eulerian path of
which do lift to an Eulerian path of  will be called admissible (with respect to T). It is clear that
will be called admissible (with respect to T). It is clear that  is admissible if and only if
is admissible if and only if  is an Eulerian path of
is an Eulerian path of . For the remainder of this section, we introduce Swan’s theorem and our main results.
. For the remainder of this section, we introduce Swan’s theorem and our main results.
Swan [1]. Let  be an Eulerian graph with d edges and k vertices satisfying
be an Eulerian graph with d edges and k vertices satisfying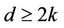 . Then
. Then  has the same number of odd and even permutations (with respect to the fixed order)
has the same number of odd and even permutations (with respect to the fixed order)
Theorem 1. Let  be an Eulerian graph with vertex set
be an Eulerian graph with vertex set  and d edges. Further let
and d edges. Further let 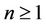 be an integer such that
be an integer such that
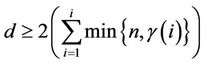 .
.
Then  is a polynomial identity on the ring
is a polynomial identity on the ring 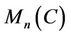 of
of 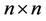 matrices over a commutative ring C with 1 Corollary 2. Let
matrices over a commutative ring C with 1 Corollary 2. Let 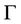 be an Eulerian graph with k vertices and d edges. Further let
be an Eulerian graph with k vertices and d edges. Further let  be an integer and assume that
be an integer and assume that . Then
. Then  is a polynomial identity on
is a polynomial identity on .
.
3. Proof of Theorem 1
Since  is multilinear, it suffices to show that
is multilinear, it suffices to show that  for any substitution T of
for any substitution T of  matrix units over C. Fix such an T and put
matrix units over C. Fix such an T and put ,
,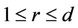 . Then
. Then
 (*)
(*)
Now consider . Clearly, and summand in (*) vanishes unless, for the given
. Clearly, and summand in (*) vanishes unless, for the given ,
,

for all , i.e., if
, i.e., if  is admissible. If so, on multiplying the matrix units, we obtain
is admissible. If so, on multiplying the matrix units, we obtain
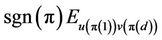 .
.
It follows that  where the inner sum is taken over all admissible permutations with
where the inner sum is taken over all admissible permutations with  and
and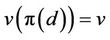 . If no such admissible
. If no such admissible  exists, the inner sum is 0 by definition. We want to prove that this inner sum is 0 anyway. It is readily seen that for any choice of u and b, a sum and
exists, the inner sum is 0 by definition. We want to prove that this inner sum is 0 anyway. It is readily seen that for any choice of u and b, a sum and  in the inner sum arises precisely of
in the inner sum arises precisely of  lifts to an Eulerian path of
lifts to an Eulerian path of  from (p, (u) to (q, v). Thus, on applying Swan’s theorem to
from (p, (u) to (q, v). Thus, on applying Swan’s theorem to 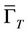 with
with  and
and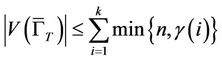 , we find that the number of even and odd admissible permutations
, we find that the number of even and odd admissible permutations  with
with  and
and  coincide whence the inner sum is 0 for any choice of u and v. This completes the proof.
coincide whence the inner sum is 0 for any choice of u and v. This completes the proof.
4. Applications
1) Let  be the Eulerian graph on one vertex with d loops. Then
be the Eulerian graph on one vertex with d loops. Then  and
and

the standard polynomial [2] in d indeterminates.
 More generally, let
More generally, let  be the Eulerian graph on k vertices with distinguished points
be the Eulerian graph on k vertices with distinguished points  and the number
and the number  of edges from vertex i to j:
of edges from vertex i to j:

Now clearly  and
and
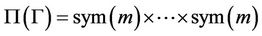 k times. On putting
k times. On putting 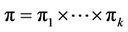 and labelling the indeterminates, corresponding to the edges from i to
and labelling the indeterminates, corresponding to the edges from i to  by
by , from the corollary 2 it follows that
, from the corollary 2 it follows that

is a polynomial identity on 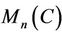 [3] if
[3] if , i.e., if
, i.e., if .
.
2) For  we define a sequence
we define a sequence ,
,  of staircase steps, and the staircase height
of staircase steps, and the staircase height . We will construct a substitution T, such that
. We will construct a substitution T, such that  lifts to the unique convering directed path of
lifts to the unique convering directed path of 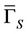 (i.e.,
(i.e., ). First define a function
). First define a function  by
by
 ;
; ,
,
 ,
, .
.
Next we define by recursion the sequence of pair ,
,  , where
, where  is a natural number and
is a natural number and  is a subset of
is a subset of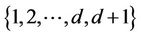 . We put
. We put  and
and . Having
. Having  in hand
in hand . There are three cases to consider:
. There are three cases to consider:
a)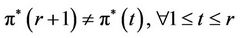 b)
b)
 ,
,  c)
c)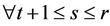
 ,
,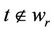 .
.
We now put

and

Let  for all
for all , it is clear that
, it is clear that  gives a substitution of
gives a substitution of  matrix units over C. Now
matrix units over C. Now

is the unique covering directed path of  from
from
 to
to  [4-7]. Since the
[4-7]. Since the 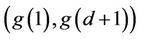 entry of the
entry of the  matrix
matrix 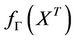 is
is , we have Theorem 3. Let
, we have Theorem 3. Let  be an Eulerian graph and
be an Eulerian graph and . If
. If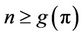 , then
, then  is not a polynomial identity on the ring
is not a polynomial identity on the ring  of
of  matrices over a commutative ring C with 1.
matrices over a commutative ring C with 1.
Remark. It is an obvious consequence of the above theorem that if  is not the least integer
is not the least integer  for which
for which  is not a polynomial identity on
is not a polynomial identity on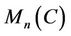 .
.
We note that, in general min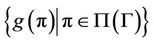 is not the least integer
is not the least integer 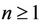 for which
for which  is not a polynomial identity on
is not a polynomial identity on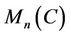 .
.
Let  be the Eulerian graph on one vertex d loops. It is easily see that
be the Eulerian graph on one vertex d loops. It is easily see that

Thus  for all
for all  and the minimality assertion of the Amitsur-Levitzki theorem follows; the main part is an immediate consequence of the corollary.
and the minimality assertion of the Amitsur-Levitzki theorem follows; the main part is an immediate consequence of the corollary.
Let  be the Eulerian graph on k vertices with distinguished points
be the Eulerian graph on k vertices with distinguished points  and the number
and the number 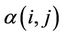 of edges from vertex i to j:
of edges from vertex i to j:

Analogously, for any  we have
we have
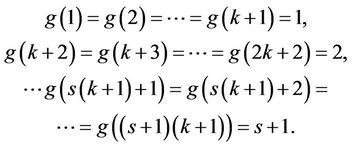
In consequence  for all
for all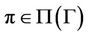 .
.
For  we get the double Capelli polynomial; it is known, however, that in this case
we get the double Capelli polynomial; it is known, however, that in this case  is not the smallest n for which
is not the smallest n for which  is not a polynomial identity on
is not a polynomial identity on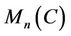 .
.
When  we use x, y and z instead of the symbols
we use x, y and z instead of the symbols ,
,  , and
, and  respectively to denote the indeterminates of the triple Capelli polynomial and continue to write m for the number of edges from vertex i to i + 1. Thus the triple Capelli polynomial is
respectively to denote the indeterminates of the triple Capelli polynomial and continue to write m for the number of edges from vertex i to i + 1. Thus the triple Capelli polynomial is